Energie potentielle de pesanteur

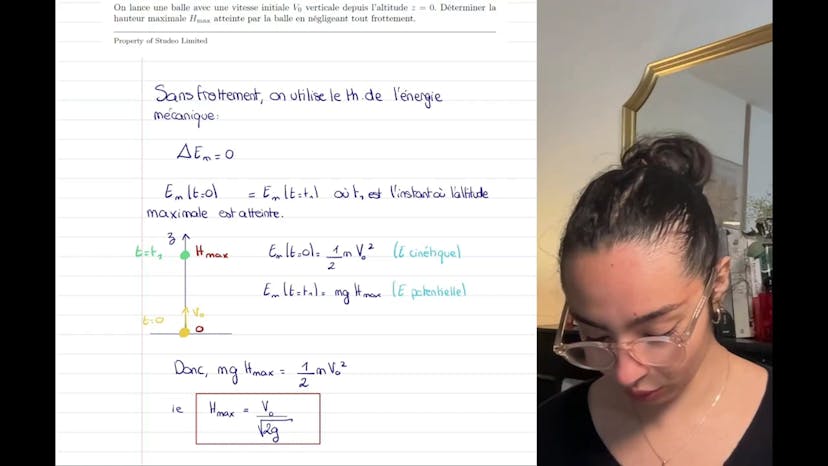
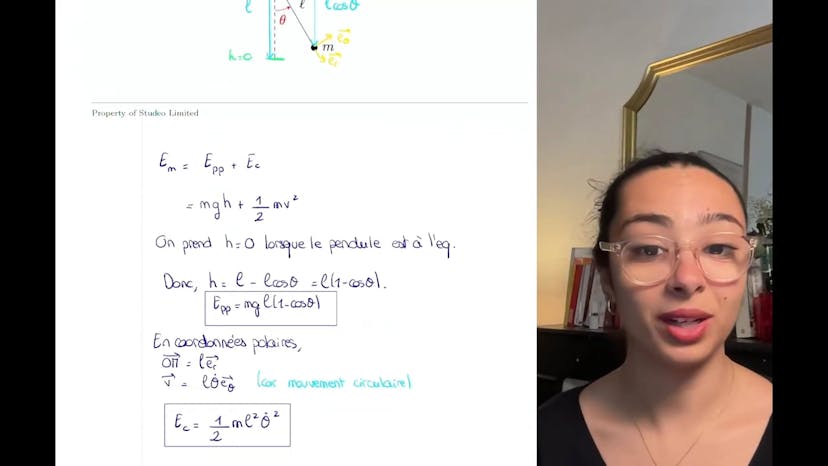
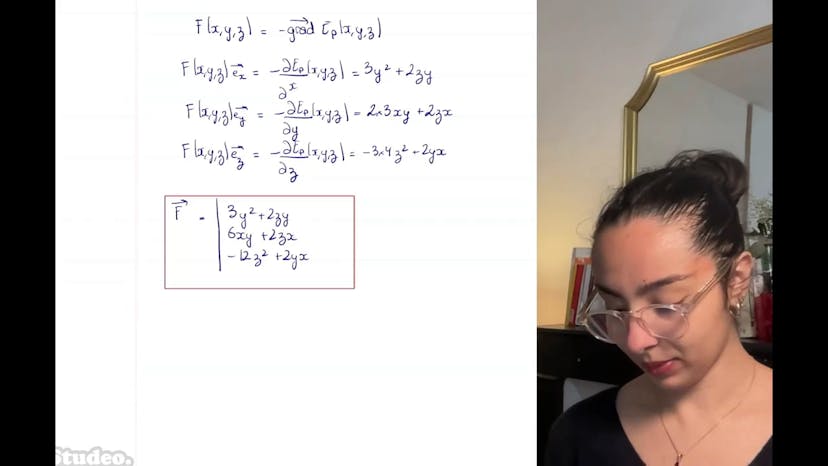
Aujourd'hui, nous allons aborder l'énergie potentielle de pesanteur dans différents systèmes de coordonnées. Dans le système cartésien, l'axe OZ est dirigé vers le haut. L'expression de l'énergie potentielle associée est donnée par EP = MgZ, où Mg représente le poids. Il est important de noter que l'expression varie selon que l'axe Z soit orienté vers le haut ou vers le bas. En coordonnées cylindriques, le poids s'exprime différemment et est donné par –Mg cosθ er – Mg sinθ eθ. L'énergie potentielle de pesanteur en coordonnées cylindriques est EP = MgR cos θ, où R représente le rayon et θ l'angle. Il est essentiel de noter que l'expression de l'énergie potentielle ne dépend que de θ en coordonnées cylindriques, et qu'elle est équivalente à celle en coordonnées cartésiennes. Les systèmes de coordonnées sont un choix arbitraire et ne doivent pas introduire de différences dans les expressions physiques. Dans notre cas, l'énergie potentielle peut être retrouvée en passant des coordonnées XYZ aux coordonnées RθZ.