Tous les sujets
Maths- Nombres et calculs
- Géométrie
- Repérage
- Vecteurs du Plan
- Droites et Systèmes d'équations
- Fonctions
- Stats et Probas
- Analyse
- Géométrie
- Probas et Stats
- Analyse (spé)
- Géométrie (spé)
- Probabilités (spé)
- Arithmétique (exp)
- Complexes (exp)
- Analyse
- Algèbre
- Analyse
- Algèbre
- Probabilités
SecondePremièreTerminale2BAC SM MarocMPSI/PCSI
Physique-Chimie
Corrigés de BAC- Prépa Examens
- Révisions Maths lycée
- Tous les sujets
- Maths
- Nombres et calculs
- Géométrie
- Repérage
- Vecteurs du Plan
- Droites et Systèmes d'équations
- Fonctions
- Stats et Probas
- Analyse
- Géométrie
- Probas et Stats
- Analyse (spé)
- Géométrie (spé)
- Probabilités (spé)
- Arithmétique (exp)
- Complexes (exp)
- Analyse
- Algèbre
- Analyse
- Algèbre
- Probabilités
SecondePremièreTerminale2BAC SM MarocMPSI/PCSI - Physique-Chimie
- Corrigés de BAC
- Prépa Examens
- Révisions Maths lycée
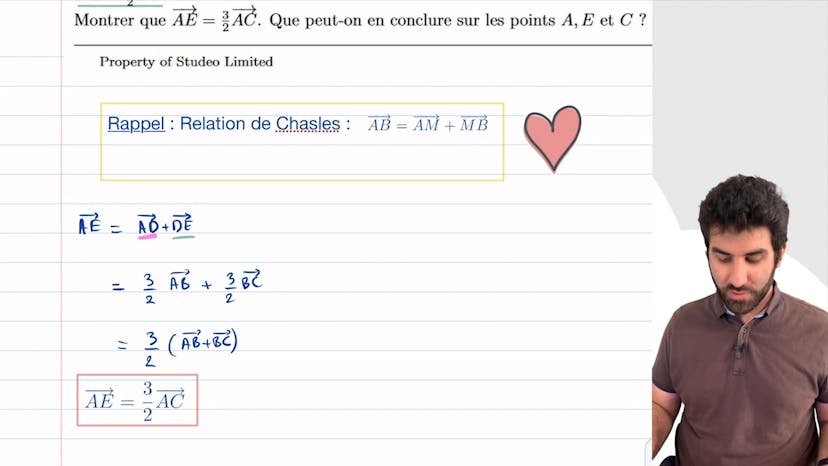
Vecteurs et alignement
Pour montrer que trois points sont alignés, on peut utiliser la méthode classique en utilisant des vecteurs. Trois points sont alignés si les vecteurs créés par ces points sont collinéaires. Deux vecteurs sont collinéaires s'il existe un coefficient de proportionnalité, k. On peut calculer les coordonnées de chaque vecteur en utilisant les formules xB-xA et yB-yA pour AB, et xC-xA et yC-yA pour AC. Ensuite, on peut observer que le vecteur AB est égal à moins 1 fois le vecteur AC, et donc AB et AC sont collinéaires. Cette propriété nous permet de conclure que les points ABC sont alignés.
