Circuit bouchon

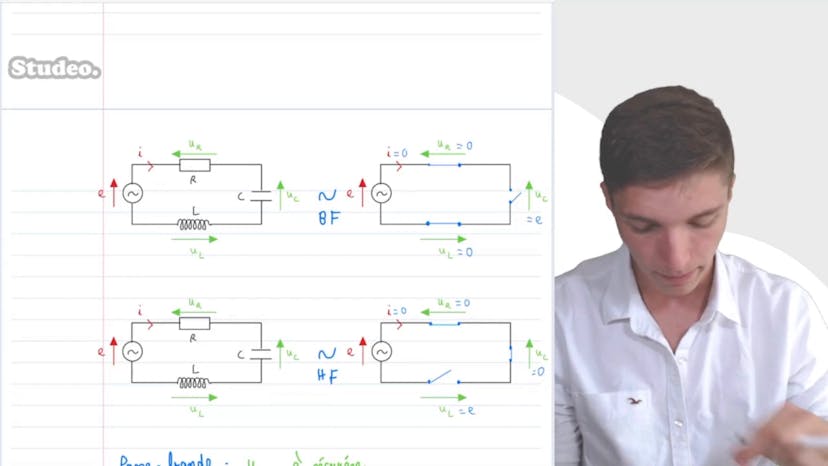
Dans cette vidéo, nous étudions le circuit Bouchon, qui est constitué d'un dipôle avec une bobine et un condensateur montés en dérivation. Nous déterminons l'impédance complexe ZS d'un dipôle RLC série en fonction des composants, de R, de la pulsation propre et du facteur de qualité. Ensuite, nous exprimons l'impédance complexe Z du dipôle parallèle sous la forme R divisé par JCωZS, facteur de 1 plus JQω sur ω0. Nous montrons que lorsque le facteur de qualité est très élevé et la pulsation pas trop faible, l'impédance peut se mettre sous la forme approchée Z est environ égal à Q²R² sur ZS complexe. Nous déterminons également que le module de l'impédance complexe est maximal lorsque la pulsation est égale à la pulsation propre ω0, et que le circuit est alors bloqué, d'où l'appellation circuit bouchon. Enfin, nous déterminons les intensités réelles qui traversent respectivement le condensateur et la bobine en fonction de E0, Q et R, et constatons que le circuit est véritablement un circuit bouchon.