Tous les sujets
Maths- Nombres et calculs
- Géométrie
- Fonctions
- Stats et Probas
- Analyse
- Géométrie
- Probas et Stats
- Analyse (spé)
- Géométrie (spé)
- Probabilités (spé)
- Arithmétique (exp)
- Complexes (exp)
- Complexes : vision algébrique
- Complexes : vision géométrique
- Analyse
- Algèbre
- Analyse
- Algèbre
- Probabilités
SecondePremièreTerminale2BAC SM MarocMPSI/PCSI
Physique-Chimie
Corrigés de BAC- Révisions Maths lycée
- Prépa Examens
- Tous les sujets
- Maths
- Nombres et calculs
- Géométrie
- Fonctions
- Stats et Probas
- Analyse
- Géométrie
- Probas et Stats
- Analyse (spé)
- Géométrie (spé)
- Probabilités (spé)
- Arithmétique (exp)
- Complexes (exp)
- Complexes : vision algébrique
- Complexes : vision géométrique
- Analyse
- Algèbre
- Analyse
- Algèbre
- Probabilités
SecondePremièreTerminale2BAC SM MarocMPSI/PCSI - Physique-Chimie
- Corrigés de BAC
- Révisions Maths lycée
- Prépa Examens
Z est-il réel ? V1
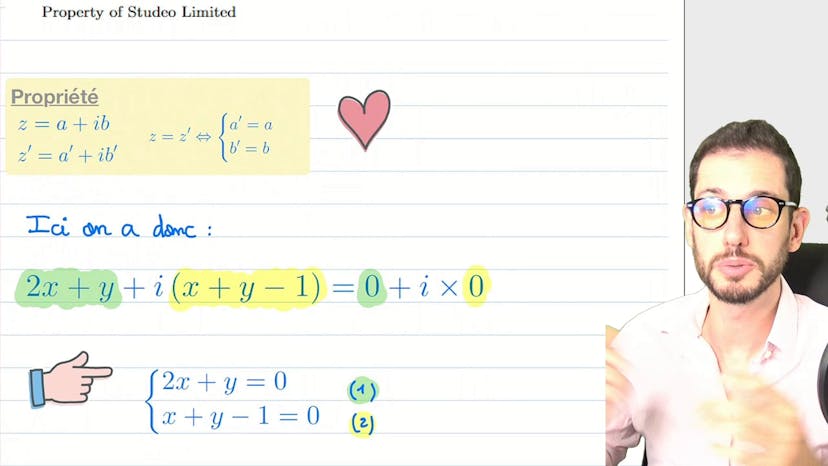
Le cours présente une méthode classique pour résoudre un exercice de complexe. L'exercice consiste à trouver l'ensemble des z tels que grand z, petit z moins 1 divisé par petit z plus 1 soit réelle. La méthode consiste à poser a et b appartenant à R, et à utiliser la propriété selon laquelle z quelconque est un réel si et seulement si la partie imaginaire de z est nulle. Les calculs sont effectués en posant petit z égal à a plus ib et en utilisant la quantité conjuguée pour simplifier l'expression. Finalement, on trouve que z est réel uniquement si b est nul, ce qui donne l'ensemble des z réels moins l'élément moins 1.
