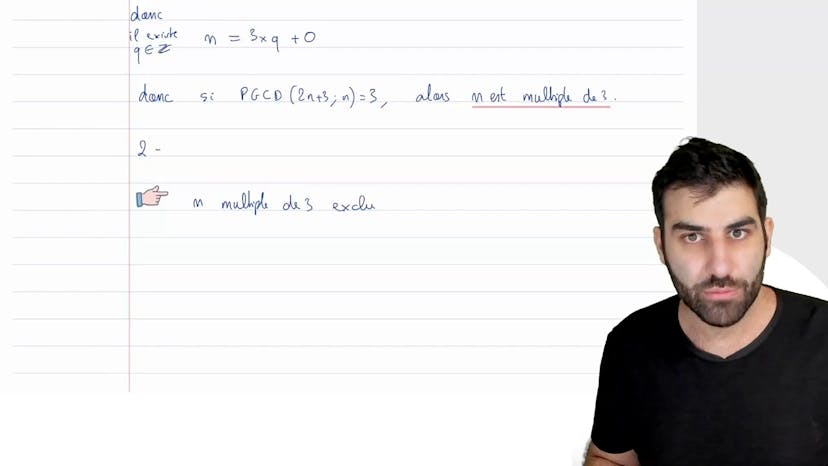Tous les sujets
Maths- Nombres et calculs
- Géométrie
- Fonctions
- Stats et Probas
- Analyse
- Géométrie
- Probas et Stats
- Analyse (spé)
- Géométrie (spé)
- Probabilités (spé)
- Arithmétique (exp)
- Divisibilité et Congruences
- PGCD
- Théorèmes de Bézout et de Gauss
- Nombres Premiers
- Complexes (exp)
- Analyse
- Algèbre
- Analyse
- Algèbre
- Probabilités
SecondePremièreTerminale2BAC SM MarocMPSI/PCSI
Physique-Chimie
Corrigés de BAC- Prépa Examens
- Révisions Maths lycée
- Tous les sujets
- Maths
- Nombres et calculs
- Géométrie
- Fonctions
- Stats et Probas
- Analyse
- Géométrie
- Probas et Stats
- Analyse (spé)
- Géométrie (spé)
- Probabilités (spé)
- Arithmétique (exp)
- Divisibilité et Congruences
- PGCD
- Théorèmes de Bézout et de Gauss
- Nombres Premiers
- Complexes (exp)
- Analyse
- Algèbre
- Analyse
- Algèbre
- Probabilités
SecondePremièreTerminale2BAC SM MarocMPSI/PCSI - Physique-Chimie
- Corrigés de BAC
- Prépa Examens
- Révisions Maths lycée
PGCD et congruences
Dans cet exercice de mathématiques, nous manipulons le PGCD et des congruences. Le système S établit que n est congruent à 1 modulo 5 et à 5 modulo 7. Nous devons montrer que si n vérifie le système S, alors il vérifie également un autre système. Nous montrons cela en utilisant des congruences et en utilisant le corollaire du théorème de Gauss. Nous en déduisons que 4n est congruent à moins 1 modulo 35, et en résolvant cette équation, nous obtenons que l'ensemble des solutions est {26 + 35k | k ∈ Z}.
