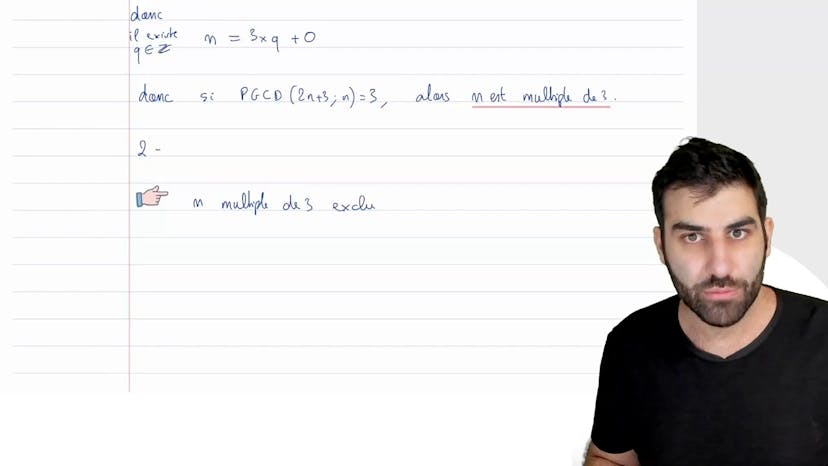Tous les sujets
Maths- Nombres et calculs
- Géométrie
- Fonctions
- Stats et Probas
- Analyse
- Géométrie
- Probas et Stats
- Analyse (spé)
- Géométrie (spé)
- Probabilités (spé)
- Arithmétique (exp)
- Divisibilité et Congruences
- PGCD
- Théorèmes de Bézout et de Gauss
- Nombres Premiers
- Complexes (exp)
- Analyse
- Algèbre
- Analyse
- Algèbre
- Probabilités
SecondePremièreTerminale2BAC SM MarocMPSI/PCSI
Physique-Chimie
Corrigés de BAC- Révisions Maths lycée
- Prépa Examens
- Tous les sujets
- Maths
- Nombres et calculs
- Géométrie
- Fonctions
- Stats et Probas
- Analyse
- Géométrie
- Probas et Stats
- Analyse (spé)
- Géométrie (spé)
- Probabilités (spé)
- Arithmétique (exp)
- Divisibilité et Congruences
- PGCD
- Théorèmes de Bézout et de Gauss
- Nombres Premiers
- Complexes (exp)
- Analyse
- Algèbre
- Analyse
- Algèbre
- Probabilités
SecondePremièreTerminale2BAC SM MarocMPSI/PCSI - Physique-Chimie
- Corrigés de BAC
- Révisions Maths lycée
- Prépa Examens
PGCD et Suite
Dans cet article, nous étudions un exercice sur le PGCD et les suites. Nous avons une suite définie sur n, avec u0 = 0 et u1 = 1, et une relation de récurrence. Nous avons également une autre suite, vn, définie comme étant un + 1 - un. Nous montrons que vn est une suite géométrique de raison 2 et que le terme initial v0 est égal à 1. Nous déduisons ensuite que pour tout entier n, un est un entier naturel et que un + 1 est égal à 2 fois un + 1. Nous utilisons ensuite une somme télescopique pour montrer que un est un entier. Enfin, nous utilisons le théorème de Bézout pour montrer que deux termes consécutifs de la suite sont premiers entre eux.
