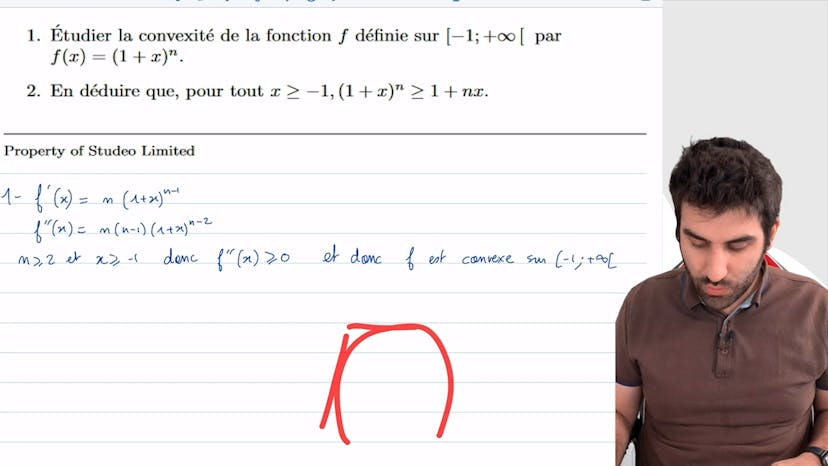
Des inégalités classiques

Dans cet exercice, on étudie différentes inégalités en utilisant les concepts de convexité et de concavité. La première inégalité à démontrer est que pour tout réel X, l'exponentiel de X est supérieur à 1+X, même si X est non nul. On commence par chercher un lien entre l'exponentiel de X et 1+X. On remarque que 1+X peut s'écrire comme l'exponentiel de 0 fois X moins 0 plus l'exponentiel de 0. On reconnaît ainsi l'équation de la tangente à la courbe de l'exponentiel de X au point d'abscisse X=0 et d'ordonnée 1. En étudiant la convexité de la fonction exponentielle, on montre que la courbe de cette fonction est strictement au-dessus de cette tangente, en dehors du point de contact. On en déduit que pour tout X réel, l'exponentiel de X est supérieur ou égal à 1+X, avec égalité seulement en X=0. Ensuite, on souhaite montrer que le logarithme de 1+X est inférieur ou égal à X. En étudiant la convexité de la fonction logarithme de 1+X, on montre qu'elle est strictement concave. On en déduit que la courbe de cette fonction est strictement en-dessous de sa tangente en X=0. On écrit donc l'équation de cette tangente et on l'utilise pour montrer que le logarithme de 1+X est inférieur ou égal à X, avec égalité en X=0. Finalement, on souhaite encadrer la fonction sinus de X entre pi/2 et X pour X dans l'intervalle [0, pi/2]. On étudie la convexité de la fonction sinus et montrons qu'elle est concave sur cet intervalle. On utilise ensuite une tangente en X=0 pour montrer que la fonction sinus de X est inférieure ou égale à X. Enfin, on utilise une corde entre les points (0, pi/2) et (pi/2, 1) pour montrer que la fonction sinus de X est supérieure ou égale à pi/2. On conclut donc que la fonction sinus de X est bien encadrée entre pi/2 et X pour X dans l'intervalle [0, pi/2].