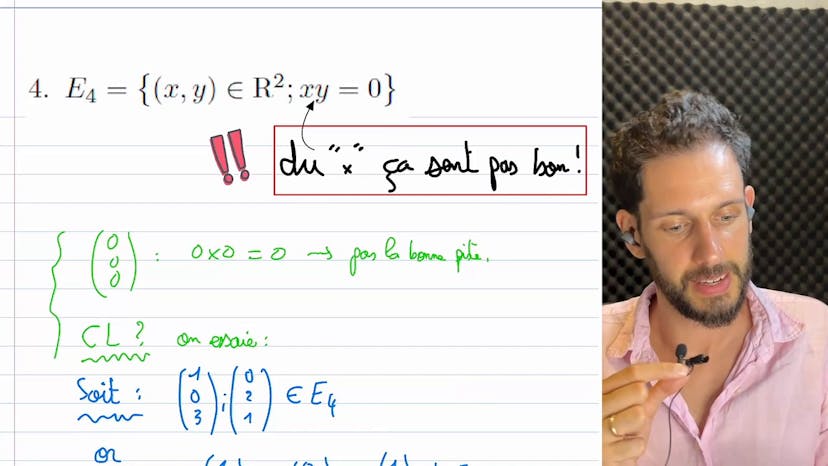Tous les sujets
Tous les sujets Maths
Maths- Nombres et calculs
- Géométrie
- Fonctions
- Stats et Probas
- Analyse
- Géométrie
- Probas et Stats
- Analyse (spé)
- Géométrie (spé)
- Probabilités (spé)
- Arithmétique (exp)
- Complexes (exp)
- Analyse
- Algèbre
- Analyse
- Algèbre
- Arithmétique dans Z
- Structures Algébriques
- Calcul matriciel et systèmes
- Espaces Vectoriels
- Matrice 2ième Partie
- Probabilités
SecondePremièreTerminale2BAC SM MarocMPSI/PCSI Physique-Chimie
Physique-Chimie Corrigés de BAC
Corrigés de BAC Révisions Maths lycée
Révisions Maths lycée Prépa Examens
Prépa Examens
 Tous les sujets
Tous les sujets Maths
Maths- Nombres et calculs
- Géométrie
- Fonctions
- Stats et Probas
- Analyse
- Géométrie
- Probas et Stats
- Analyse (spé)
- Géométrie (spé)
- Probabilités (spé)
- Arithmétique (exp)
- Complexes (exp)
- Analyse
- Algèbre
- Analyse
- Algèbre
- Arithmétique dans Z
- Structures Algébriques
- Calcul matriciel et systèmes
- Espaces Vectoriels
- Matrice 2ième Partie
- Probabilités
SecondePremièreTerminale2BAC SM MarocMPSI/PCSI Physique-Chimie
Physique-Chimie Corrigés de BAC
Corrigés de BAC Révisions Maths lycée
Révisions Maths lycée Prépa Examens
Prépa Examens
Est-ce un EV ? Avec un SEV
Le cours concerne les espaces vectoriels et présente des techniques pour montrer si un espace est un espace vectoriel ou non. Il y a deux techniques principales :
1) Montrer que l'espace est un sous-espace vectoriel d'un espace vectoriel connu en vérifiant trois propriétés : l'inclusion dans un espace vectoriel, la conservation des éléments par combinaison linéaire et la présence de zéro dans l'espace.
2) Montrer que l'ensemble peut être écrit comme un VECT (ensemble des combinaisons linéaires) puisque tous les VECTS sont des espaces vectoriels.
Il est également possible d'utiliser la notion de noyau d'une application linéaire pour montrer qu'un espace est un espace vectoriel.
Le cours présente plus en détail la technique 1 pour un exemple spécifique où l'ensemble E1 est l'ensemble des vecteurs de R3 dont les coordonnées vérifient une équation donnée. Les trois critères sont vérifiés pour montrer que E1 est un sous-espace vectoriel de R3.