Cours de Dérivation et étude de fonctions en Ligne par les Meilleurs Professeurs - Dérivation et étude de fonctions

Équation Tangente

Ce cours porte sur la détermination des équations de tangentes, une méthode classique en mathématiques. Il est important de bien maîtriser cette méthode car elle est souvent utilisée dans les exercices d'étude de fonctions pour analyser les tangentes et la position relative de la courbe par rapport à ces tangentes. Dans cet exercice, on nous demande d'étudier une fonction f(x) = x^2 + 3x + 1 et de calculer f'(2) et f(2). Après calcul, on trouve que f(2) = 11 et f'(2) = 7. En utilisant la formule y = f'(A)x + f(A) (A ici étant égal à 2), on trouve l'équation de la tangente : y = 7x + 3. Il est intéressant de comprendre d'où vient cette formule. Pour cela, on peut réexprimer une équation de droite y = mx + p en utilisant les coordonnées du point de tangence A (qui ici est 2, f(2)) et la pente de la tangente (qui est égale à la dérivée de f en A). On obtient ainsi l'équation y = f'(A)x + (f(A)-Af'(A)). Finalement, nous devons étudier une autre question concernant la fonction g(x) = e^x et l'équation de sa tangente en un point donné (ici le point (0,1)). Après calcul, on trouve l'équation de la tangente : y = x + 1. En résumé, ce cours nous a permis d'apprendre la méthode de détermination des équations de tangentes, une compétence essentielle dans l'étude des fonctions.

Formules Classiques

Dans ce cours, il est rappelé l'importance de connaître parfaitement les formules de dérivation, car des erreurs sur ces formules peuvent entraîner de mauvais résultats dans un contrôle ou un examen. Il est donc essentiel d'être sûr de ses formules. Quelques exemples sont donnés pour illustrer le fonctionnement des dérivées. Pour une fonction de la forme x^n, la dérivée est n fois x^(n-1). Pour une fonction de la forme √x, la dérivée est (1/2)√x. Pour une fonction de la forme 1/v, la dérivée est -v'/(v^2). Pour une fonction de la forme uv, la dérivée est u'v + uv'. Il est conseillé de factoriser autant que possible lors des calculs, sauf si cela s'avère compliqué. Il est également recommandé de développer et de regrouper les termes de même degré pour faciliter les calculs et éviter les erreurs. Une méthode systématique de sélection des termes peut être utile pour être sûr de ne pas en oublier. En conclusion, il est rappelé l'importance de bien maîtriser les formules de dérivation et de s'entraîner régulièrement pour les mémoriser.

Polynômes 2nd Degré

Dans ce cours, nous étudions la méthode d'étude d'un polynôme de degré 2 de manière plus rapide que la méthode traditionnelle. Nous prenons comme exemple le polynôme 2x²-8x±. Nous commençons par justifier l'ensemble de dérivabilité de la fonction f, puis nous calculons sa dérivée qui est 4x-8. Pour étudier le signe de la dérivée, nous factorisons par 4 et remarquons que le signe change en x=2. Ainsi, f'x est positif lorsque x est supérieur à 2 et négatif lorsque x est inférieur à 2. En utilisant ces informations, nous pouvons établir le tableau de variation de la fonction. Nous calculons ensuite l'image de l'extrémum qui est un minimum en x=2, où f'2=7. Pour aller plus vite, nous utilisons une astuce basée sur les connaissances générales des polynômes de degré 2. Nous savons que ces polynômes s'écrivent sous la forme ax²+bx+c et que l'extrémum est atteint en -b/2a. En observant le signe de a, nous pouvons déterminer si l'extrémum est un minimum ou un maximum. Dans notre exemple, a étant positif, nous savons que l'extrémum est un minimum. Ainsi, sans avoir à dériver, nous pouvons conclure que la fonction est d'abord décroissante, puis croissante, et que les coordonnées du minimum sont -b/2a=2, confirmant notre résultat précédent. Nous pouvons également utiliser ces résultats pour déterminer le signe de la fonction. Nous utilisons les coordonnées de l'extrémum (-b/2a) ou l'expression -Δ/4a pour calculer l'ordonnée. De plus, nous connaissons les racines du polynôme (-b+√Δ/2a et -b-√Δ/2a). Ainsi, nous observons que le minimum est situé au centre et que les racines sont symétriquement éloignées du centre. Cette astuce nous permet de rapidement déduire le sens de variation et le signe de la fonction lorsque nous rencontrons un polynôme de degré 2. Pour plus d'informations, nous pouvons consulter la FAQ.

Étude f : Niveau MPSI mais outils de première !

Le cours porte sur l'étude d'une famille de fonctions de la forme E(2x)/x^n, où n est un entier naturel non nul. Tout d'abord, il est demandé de déterminer le plus grand ensemble de définition de la fonction f. Cela est relativement simple, car il suffit d'éviter que le dénominateur soit nul. Ensuite, il est demandé de déterminer le plus grand ensemble de dérivabilité de f. Étant donné que f est le produit d'une exponentielle et d'une fraction de polynôme, f sera dérivable sur tout son ensemble de définition. Ensuite, en supposant que n est pair, il est demandé de dresser le tableau de variation de f sans indication des limites aux bornes. Pour cela, on étudie la dérivée de f, qui est obtenue en utilisant la règle du quotient. On factorise certains termes et on constate que le changement de signe se produit en 0 et en 2p. On en déduit le tableau de variation de f. Ensuite, les limites de f aux bornes sont calculées. Pour les limites en plus et moins l'infini, le résultat est directement obtenu en utilisant la croissance comparée. Pour les limites en 0 plus et 0 moins, on analyse les termes de la fonction f et on conclut que ces limites tendent vers plus l'infini. Enfin, le même processus est effectué pour le cas où n est impair. On constate que le tableau de variation est différent et que les limites en 0 plus et 0 moins tendent vers moins l'infini. Ce cours met l'accent sur l'importance de faire une distinction de cas et illustre les différentes étapes de l'étude de fonctions et de limites.

Composition : Déf

Dans cette vidéo, l'auteur explique la composition de deux fonctions. Il commence par donner un exemple concret, en décomposant la fonction racine de x² plus 7 en trois étapes. Ensuite, il donne une définition théorique de la composition de fonctions, en notant VU comme la fonction définie par V2U2x. Il explique ensuite les propriétés de la composition de fonctions, notamment l'associativité et le fait que la composition n'est pas commutative. Il donne un exemple concret pour montrer que V rond U est différent de U rond V dans la plupart des cas. Il conclut en rappelant que la composition de fonctions n'est pas commutative et invite les spectateurs à poser des questions dans le forum.

Dériver une composée

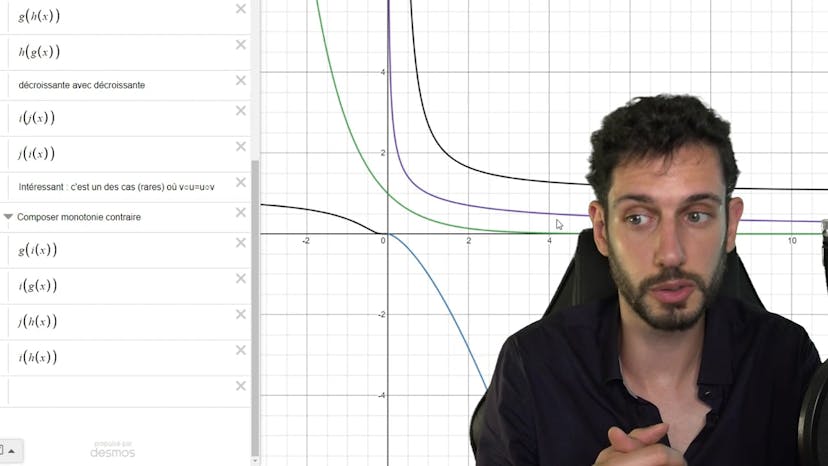
Dans cette vidéo, nous allons voir comment dériver une fonction composée. Avant de commencer, rappelons rapidement ce qu'est la composition. En première, nous avons déjà vu les bases de la composition, mais maintenant nous allons approfondir notre compréhension théorique. La composition nécessite certaines contraintes sur les ensembles d'arrivée et de départ des fonctions que nous composons. Pour dériver une fonction composée, nous allons reprendre des exemples que nous connaissons déjà. Au lieu de nous lancer directement dans une formule théorique, nous préférons commencer par des exemples plus simples. Reprenons l'exemple de la fonction 1/x, nous savons déjà que sa dérivée est -1/x^2. Donc, intuitivement, nous pourrions penser que la dérivée de 1/u est -1/u^2. Cependant, cela n'est pas correct. En réalité, la bonne formule est 1/u' = -u'/u^2. Nous devons toujours prendre en compte le facteur u' dans notre formule. Poursuivons avec l'exemple de la racine de x. Nous savons que la dérivée de la racine de x est 1/(2√x). Une fois de plus, intuitivement, nous pourrions penser que la dérivée de la racine de u est 1/(2√u). Mais nous devons prendre en compte le facteur u'. La bonne formule est u'/(2√u). Nous voyons ici un motif se dessiner : le facteur intuitif que nous connaissons, multiplié par u'. Si nous continuons, nous pouvons rappeler que la dérivée de e^u est e^u * u'. Voici un tableau récapitulatif des différentes dérivées : a*u+b = a*u' + b, u^2 = 2*u*u', u^3 = 3*u^2*u', u^n = n*u^(n-1) * u', 1/u = -1/u^2 * u', etc. Il y a toujours ce facteur u' qui s'ajoute. La formule générale se résume donc à : v o u' = v' o u * u'. Une conséquence intéressante est que si v et u ont la même monotonie (toutes les deux croissantes ou toutes les deux décroissantes), alors la fonction composée v o u est croissante. Par contre, si elles ont des monotonies opposées (une croissante et une décroissante), alors la fonction composée v o u est décroissante. Nous pouvons également voir cela à travers quelques exemples graphiques. J'espère que tout cela est clair, n'hésitez pas à poser des questions sur le forum. Bon entraînement avec les vidéos de méthodes et à la prochaine !