 Tous les sujets
Tous les sujets Maths
Maths- Nombres et calculs
- Géométrie
- Fonctions
- Stats et Probas
- Analyse
- Géométrie
- Probas et Stats
- Analyse (spé)
- Géométrie (spé)
- Probabilités (spé)
- Arithmétique (exp)
- Complexes (exp)
- Analyse
- Algèbre
- Analyse
- Logique
- Ensembles
- Applications & Relations
- Logique : Sujets d'écrits
- Calcul Algébrique
- Trigonométrie
- Calcul et trigo : Sujets d'écrits
- Complexes : Définitions Rappels
- Complexes : Formes trigo, expo
- Complexes : Equations & polynômes
- Complexes : Géométrie
- Complexes : Sujets d'écrits
- Fonctions (0) : Généralités
- Fonctions (0) : Dérivation, classe C1
- Fonctions (0) usuelles
- Fonctions (0) : Sujets d'écrits
- Calcul de primitives
- EDL du 1er ordre
- EDL 2nd ordre à coéffs constants
- Primitives & EDL : Sujets d'écrits
- Nombres Réels
- Suites et Convergence
- Suites : applications avancées
- Suites : Sujets d'écrits
- Limites
- Continuité en un point
- Continuité sur un segment
- Fonctions (1) : Sujets d'écrits
- Fonctions (2) : classe Ck
- Rolle & Accroissements Finis
- Fonctions (2) : Sujets d'écrits
- Fonctions (3) : Généralités
- Fonctions (3) : Sujets d'écrits
- Équivalence et Suites
- Équivalence et Fonctions
- Développements Limités
- Algèbre
- Probabilités
SecondePremièreTerminale2BAC SM MarocMPSI/PCSI Physique-Chimie
Physique-Chimie Corrigés de BAC
Corrigés de BAC Révisions Maths lycée
Révisions Maths lycée Prépa Examens
Prépa Examens
Terminale
Première
Seconde
MPSI/PCSI
2BAC SM Maroc
 Tous les sujets
Tous les sujets Maths
Maths- Nombres et calculs
- Géométrie
- Fonctions
- Stats et Probas
- Analyse
- Géométrie
- Probas et Stats
- Analyse (spé)
- Géométrie (spé)
- Probabilités (spé)
- Arithmétique (exp)
- Complexes (exp)
- Analyse
- Algèbre
- Analyse
- Logique
- Ensembles
- Applications & Relations
- Logique : Sujets d'écrits
- Calcul Algébrique
- Trigonométrie
- Calcul et trigo : Sujets d'écrits
- Complexes : Définitions Rappels
- Complexes : Formes trigo, expo
- Complexes : Equations & polynômes
- Complexes : Géométrie
- Complexes : Sujets d'écrits
- Fonctions (0) : Généralités
- Fonctions (0) : Dérivation, classe C1
- Fonctions (0) usuelles
- Fonctions (0) : Sujets d'écrits
- Calcul de primitives
- EDL du 1er ordre
- EDL 2nd ordre à coéffs constants
- Primitives & EDL : Sujets d'écrits
- Nombres Réels
- Suites et Convergence
- Suites : applications avancées
- Suites : Sujets d'écrits
- Limites
- Continuité en un point
- Continuité sur un segment
- Fonctions (1) : Sujets d'écrits
- Fonctions (2) : classe Ck
- Rolle & Accroissements Finis
- Fonctions (2) : Sujets d'écrits
- Fonctions (3) : Généralités
- Fonctions (3) : Sujets d'écrits
- Équivalence et Suites
- Équivalence et Fonctions
- Développements Limités
- Algèbre
- Probabilités
SecondePremièreTerminale2BAC SM MarocMPSI/PCSI Physique-Chimie
Physique-Chimie Corrigés de BAC
Corrigés de BAC Révisions Maths lycée
Révisions Maths lycée Prépa Examens
Prépa Examens
Maths
Analyse
MPSI/PCSI
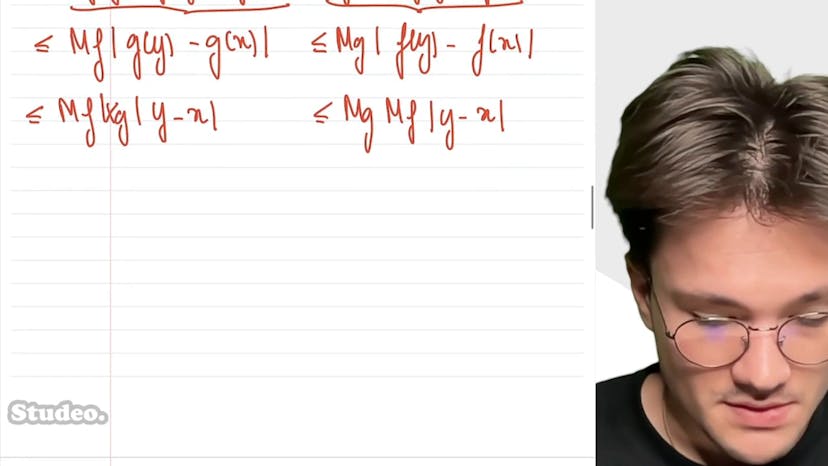
Type Mines : Partie A - 1/4
Dans cette vidéo, Corentin nous présente un exercice sur les fonctions Lipschitzschiene en mathématiques. Il commence par définir les termes et notations importants, puis explore les différentes questions de l'exercice. La première question demande de montrer que l'ensemble des fonctions Lipschitzschiene est non vide et stable par combinaison linéaire. La deuxième question demande de montrer que la composition de deux fonctions Lipschitzschiene est également une fonction Lipschitzschiene. La troisième question explore l'idée que si deux fonctions sont bornées, leur produit est également une fonction Lipschitzschiene. Enfin, Corentin présente un contre-exemple pour prouver que le produit de deux fonctions Lipschitzschiene n'est pas toujours Lipschitzschiene.
Maths
Analyse
MPSI/PCSI

Type Mines : Partie A - 2/4
Ce cours traite de la démonstration de l'existence de deux réels positifs a et b pour toute fonction Lipschitzienne f, telle que pour tout réel x, la valeur absolue de f de x soit inférieure ou égale à a fois la valeur absolue de x plus b. La démonstration repose sur une inégalité triangulaire et sur le caractère Lipschitzien de f. Ensuite, le cours aborde la question de la généralisation de cette propriété pour toutes les fonctions vérifiant que pour tout réel x et y, ayant une distance inférieure ou égale à 1, on a f de y moins f de x inférieur ou égal à m fois y moins x. Pour cela, il est nécessaire de montrer que la fonction en question appartient à l'ensemble des fonctions Lipschitzienne. La démonstration passe par une décomposition et une majoration de la différence de f entre deux réels x et y, d'une distance strictement supérieure à 1, en utilisant une combinaison télescopique et l'inégalité triangulaire. Finalement, la propriété Lipschitzienne est établie, et la fonction est montrée comme étant m-lipschitzienne.
Maths
Analyse
MPSI/PCSI

Type Mines : Partie A - 3/4
Dans ce cours, Corentin parle de la Lipschitzianité et de l'uniformité de continuité des fonctions. Il commence par montrer que si une fonction est Lipschitzienne et qu'un réel alpha est ajouté à son argument, alors la nouvelle fonction obtenue est aussi Lipschitzienne. Ensuite, il montre que la fonction sinus est Lipschitzienne et que sa fonction dérivée, le cosinus, est également Lipschitzienne. Finalement, il explique ce qu'est une application uniformément continue et montre que si une fonction est Lipschitzienne, alors elle est également uniformément continue. Il prouve ensuite que la réciproque, à savoir qu'une fonction uniformément continue n'est pas forcément Lipschitzienne, est fausse. Il illustre cela par un exemple de fonction uniformément continue mais non Lipschitzienne, la fonction valeur absolue de x à la racine.
Maths
Analyse
MPSI/PCSI

Type Mines : Partie B - 4/4
Dans cette vidéo, Corentin traite de la recherche de solutions Lipschitzienne d'une équation donnée. Il commence par montrer qu'une équation vérifiée pour tout réel X et tout entier naturel N peut être résolue par récurrence sur N. Ensuite il démontre que cette équation ne permet au plus qu'une solution dans l'ensemble des fonctions Lipschitzienne lorsque la valeur absolue de lambda est strictement inférieure à 1. Lorsque f est une fonction constante de valeur 1, la solution Lipschitzienne unique est trouvée en résolvant l'équation et en montrant qu'elle est constante. Enfin, Corentin démontre que la fonction donnée par une formule particulière est la solution unique Lipschitzienne de l'équation lorsque f est égale à cosinus et sinus de x.
Mathématiques
Analyse
ECG
Type Mines : Partie A - 1/4
Aucun résumé n'est disponible pour cette vidéo
Mathématiques
Analyse
ECG
Type Mines : Partie A - 2/4
Aucun résumé n'est disponible pour cette vidéo
Mathématiques
Analyse
ECG
Type Mines : Partie A - 3/4
Aucun résumé n'est disponible pour cette vidéo
Mathématiques
Analyse
ECG
Type Mines : Partie B - 4/4
Aucun résumé n'est disponible pour cette vidéo
Mathématiques
Analyse
BCPST
Type Mines : Partie A - 1/4
Aucun résumé n'est disponible pour cette vidéo
Mathématiques
Analyse
BCPST
Type Mines : Partie A - 2/4
Aucun résumé n'est disponible pour cette vidéo
Mathématiques
Analyse
BCPST
Type Mines : Partie A - 3/4
Aucun résumé n'est disponible pour cette vidéo
Mathématiques
Analyse
BCPST
Type Mines : Partie B - 4/4
Aucun résumé n'est disponible pour cette vidéo
Maths Approfondies
Analyse
ECG
Type Mines : Partie A - 1/4
Aucun résumé n'est disponible pour cette vidéo
Maths Approfondies
Analyse
ECG

Type Mines : Partie A - 2/4
Aucun résumé n'est disponible pour cette vidéo
Maths Approfondies
Analyse
ECG

Type Mines : Partie A - 3/4
Aucun résumé n'est disponible pour cette vidéo
Maths Approfondies
Analyse
ECG

Type Mines : Partie B - 4/4
Aucun résumé n'est disponible pour cette vidéo
Maths Appliquées 1
Analyse
ECG
Type Mines : Partie A - 1/4
Aucun résumé n'est disponible pour cette vidéo
Maths Appliquées 1
Analyse
ECG

Type Mines : Partie A - 2/4
Aucun résumé n'est disponible pour cette vidéo
Maths Appliquées 1
Analyse
ECG

Type Mines : Partie A - 3/4
Aucun résumé n'est disponible pour cette vidéo
Maths Appliquées 1
Analyse
ECG

Type Mines : Partie B - 4/4
Aucun résumé n'est disponible pour cette vidéo


