 Tous les sujets
Tous les sujets Maths
Maths- Nombres et calculs
- Géométrie
- Fonctions
- Stats et Probas
- Analyse
- Géométrie
- Probas et Stats
- Analyse (spé)
- Géométrie (spé)
- Probabilités (spé)
- Arithmétique (exp)
- Complexes (exp)
- Analyse
- Algèbre
- Analyse
- Logique et ensembles
- Calcul algébrique et trigonométrie
- Complexes
- Fonctions d'une variable réelle (0)
- Primitives et équations différentielles
- Nombres réels et suites numériques
- Fonctions : Limites et continuité (1)
- Fonctions : dérivabilité (2)
- Fonctions : convexité (3)
- Analyse Asymptotique
- Algèbre
- Probabilités
SecondePremièreTerminale2BAC SM MarocMPSI/PCSI Physique-Chimie
Physique-Chimie Corrigés de BAC
Corrigés de BAC Révisions Maths lycée
Révisions Maths lycée Prépa Examens
Prépa Examens
Terminale
Première
Seconde
MPSI/PCSI
2BAC SM Maroc
 Tous les sujets
Tous les sujets Maths
Maths- Nombres et calculs
- Géométrie
- Fonctions
- Stats et Probas
- Analyse
- Géométrie
- Probas et Stats
- Analyse (spé)
- Géométrie (spé)
- Probabilités (spé)
- Arithmétique (exp)
- Complexes (exp)
- Analyse
- Algèbre
- Analyse
- Logique et ensembles
- Calcul algébrique et trigonométrie
- Complexes
- Fonctions d'une variable réelle (0)
- Primitives et équations différentielles
- Nombres réels et suites numériques
- Fonctions : Limites et continuité (1)
- Fonctions : dérivabilité (2)
- Fonctions : convexité (3)
- Analyse Asymptotique
- Algèbre
- Probabilités
SecondePremièreTerminale2BAC SM MarocMPSI/PCSI Physique-Chimie
Physique-Chimie Corrigés de BAC
Corrigés de BAC Révisions Maths lycée
Révisions Maths lycée Prépa Examens
Prépa Examens
Maths
Analyse
MPSI/PCSI
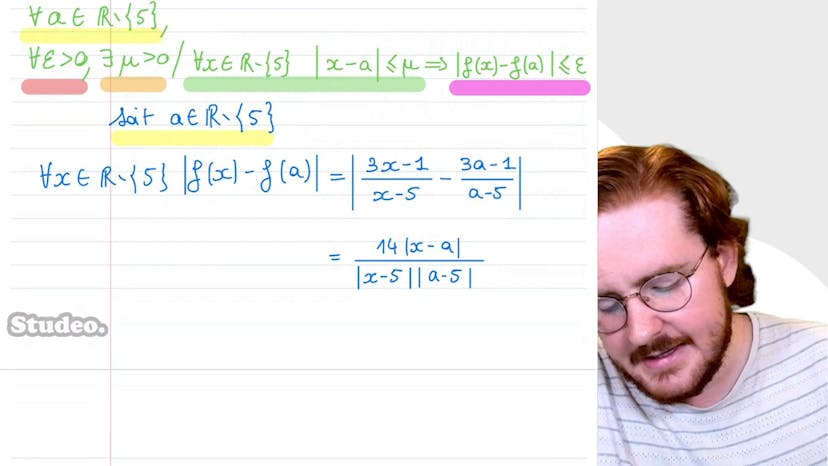
Limite et continuité avec la définition formelle
Paul présente un exercice de manipulation des définitions de limite et de continuité. Le but est de montrer, en utilisant uniquement la définition, que la limite de 3x-1 sur x-5 quand x tend vers 5 par valeur supérieure est égale à plus l'infini. Paul rappelle la définition de la limite et montre comment trouver epsilon en utilisant le fait que x est supérieur ou égal à 5. Ensuite, Paul montre comment prouver la continuité de la fonction en tous points de l'ensemble de définition, à l'exception de 5. Pour cela, il utilise la définition de la continuité et exprime f de x moins f de A en fonction de x moins A. Il restreint ensuite l'ensemble de x et choisit mu pour contrôler x moins A. Enfin, il montre que f de x moins f de A est inférieur ou égal à epsilon en choisissant le mu approprié.
Maths
Analyse
MPSI/PCSI

Détermination d'une limite à l'aide de la définition formelle
Dans cet exercice de mathématiques, on cherche à démontrer que la limite d'une fonction bornée est égale à 0. Pour cela, on utilise la définition de la limite, puis on procède par l'absurde. On suppose que la limite est strictement supérieure à 0 et on montre que cela entraîne une contradiction car la fonction dépasserait sa borne. Finalement, on conclut que la limite est bien égale à 0.
Maths
Analyse
MPSI/PCSI

Limites de fonctions sinus
Dans cette vidéo sur les limites et la prolongation par continuité des fonctions, on aborde le comportement des sinus en limites. On commence par montrer que la fonction x*sin(x) n'a pas de limite en plus infini en utilisant une technique d'absurde. Ensuite, on montre que la fonction x*sin(1/x) n'a pas de limite en 0 en utilisant des suites. Enfin, on démontre que la fonction x*sin(1/x) est prolongeable par continuité en 0 en utilisant le théorème d'existence de la limite par encadrement. La limite est trouvée et vaut 0, ce qui permet de prolonger la fonction. Cette vidéo est un excellent guide pour comprendre les limites et la continuité des fonctions trigonométriques.
Maths
Analyse
MPSI/PCSI

Calculs de limites
Dans cette leçon, on apprend à calculer les limites de certaines fonctions. La première étape est de déterminer la forme de la limite, qui peut être indéterminée. Il peut être nécessaire de manipuler l'expression pour faire apparaître la limite. Les techniques courantes comprennent la factorisation par le terme dominant pour les termes avec des puissances différentes et la multiplication par la conjugaison pour les racines. Une analyse rapide est nécessaire car le calcul de la limite doit être rapide. Dans les exemples donnés, la limite a été trouvée pour être plus l'infini, moins 1 huitième, 1, 5 sixièmes et 1 demi.
Maths
Analyse
MPSI/PCSI

Limites de parties entières
Dans cette vidéo, Paul étudie les limites à droite des fonctions f(x), g(x) et h(x) qui sont associées aux parties entières de 1/x, x × partie entière de 1/x et x^2 × partie entière de 1/x. En utilisant le théorème de comparaison et le théorème d'existence de la limite par encadrement, Paul démontre que la limite à droite de f(x) en 0 est plus l'infini, la limite à droite de g(x) en 0 est 1 et la limite à droite de h(x) en 0 est 0.
Maths
Analyse
MPSI/PCSI

Détermination d'une limite à l'aide de la définition formelle
Bonjour, je suis Paul et je vais résumer ce cours en utilisant des techniques d'optimisation pour le référencement naturel (SEO). Dans cette vidéo, nous abordons un exercice complexe sur les continuités et les limites. L'énoncé est le suivant : si f(x+1) - f(x) converge vers une limite réelle L lorsque x tend vers l'infini, nous devons montrer que f(x)/x a également la même limite L.
Pour résoudre cet exercice, nous commençons par écrire f(x+1) - f(x) convergent vers L. En manipulant cette inégalité, nous obtenons f(x)/x avec des termes qui tendent vers 0. Cependant, nous ne pouvons pas directement utiliser ces informations pour prouver notre résultat.
L'idée clé est de sommer cette inégalité sur un n choisi judicieusement, puis de contrôler ces termes pour éviter qu'ils tendent vers 0. Nous utilisons la continuité de f à un certain moment pour borner la fonction et l'écraser avec x tendant vers 0.
En résumé, nous démontrons que f(x)/x converge vers L en utilisant des encadrements pour contrôler les termes qui tendent vers 0 et en jouant sur la continuité de f pour borner la fonction.
J'espère que vous avez bien suivi. N'hésitez pas à revoir l'exercice si vous avez des questions. À la prochaine fois !
Maths
Analyse
MPSI/PCSI

Caractérisation séquentielle de la limite
Dans cet exercice sur les limites et la continuité, nous avons une fonction f continue en 0. Nous prenons un a dans R et posons un égal à f de a sur 2n. Nous devons déterminer la suite un et en déduire l'expression de f. Nous remarquons que a sur 2n tend vers 0, le point de continuité de f. Nous pouvons donc utiliser la définition séquentielle de la limite en remplaçant x par la suite un. Nous remarquons aussi que f de x est égal à f de 2x. En utilisant ces deux éléments, nous montrons que la suite un est constante et égale à f de a. Par la continuité de f en 0 et le fait que la limite de a sur 2n tend vers 0, nous montrons que f de a est égal à f de 0 pour tout a dans R. Cela prouve que f est constante.
Maths
Analyse
MPSI/PCSI

Limites de parties entières
Dans cette vidéo, Paul explique comment les limites de fonctions écrites avec des parties entières se comportent en zéro. Pour la fonction f, il montre que la limite existe et est égale à b/a. Pour la fonction g, il montre que la limite n'existe pas car elle a un comportement différent lorsqu'elle tend vers zéro par valeur positive et négative. Lorsqu'elle tend vers zéro par valeur positive, elle tend vers zéro, alors qu'elle tend vers plus l'infini lorsqu'elle tend vers zéro par valeur négative.
Maths
Analyse
MPSI/PCSI

Continuité en un point
Dans cette vidéo, Paul traite de la continuité de la fonction g sur R. La fonction g est définie comme étant égale à 1 sur l'hégaryme de valeur absolue de x si x n'est pas égale à moins 1, 0 ou 1, et 0 si x est égale à moins 1, 0 ou 1. La question posée est de savoir en quels points g est continue. Dans un premier temps, Paul traite le cas où x appartient à R privé de moins 1, 0 ou 1, et il montre que g est continue sur cette partie de R. Il étudie ensuite la continuité de g en moins 1, 0 et 1. Il montre que g est continue en 0, mais pas en 1 et moins 1. Par conséquent, la fonction g est continue sur R privé de moins 1 et 1.
Maths
Analyse
MPSI/PCSI

Continuité avec paramètres
Dans cette vidéo, on explore la continuité de fonctions et on étudie pour quelle valeur de a la fonction f est continue, ainsi que pour quelle valeur alpha, beta et gamma les fonctions g sont continues. On vérifie également que les morceaux de fonctions sont bien raccordés entre eux, et pour quelles valeurs de constantes. La fonction f est continue sur r privé de 1 pour a=1 ou 0, et g est continue sur r privé de 0 et 1 pour alpha, beta et gamma appartenant à l'ensemble x 1 moins x, x pour x appartenant à R.
Maths
Analyse
MPSI/PCSI

Prolongements par continuité de fonctions cosinus et sinus
Dans cette vidéo, Paul étudie le prolongement par continuité de fonctions contenant des sinus et des cosinus. Il commence par examiner si la fonction f2x = sinx*sin(1/x) est prolongeable par continuité à R entier. En appliquant une inégalité et en montrant que la limite en 0 est bornée, il conclut que la fonction est bien prolongeable par continuité. En revanche, lorsqu'il examine la fonction g = cos(x)*cos(1/x), il constate que cette fonction ne peut être prolongeable par continuité car cos(1/x) tend vers 1 en 0, ce qui ne permet pas d'écraser les oscillations. Paul utilise la méthode de considération de deux suites qui tendent vers 0 mais dont les limites diffèrent, pour prouver que la limite de g en 0 n'existe pas. Enfin, Paul étudie la fonction h = sin(x+1)*ln(1+x) qui présente une forme indéterminée en -1. En appliquant une astuce pour ramener la limite en 0, il montre que la fonction est prolongeable par continuité. Ainsi, il conclut que h est bien prolongeable par continuité sur R.
Maths
Analyse
MPSI/PCSI
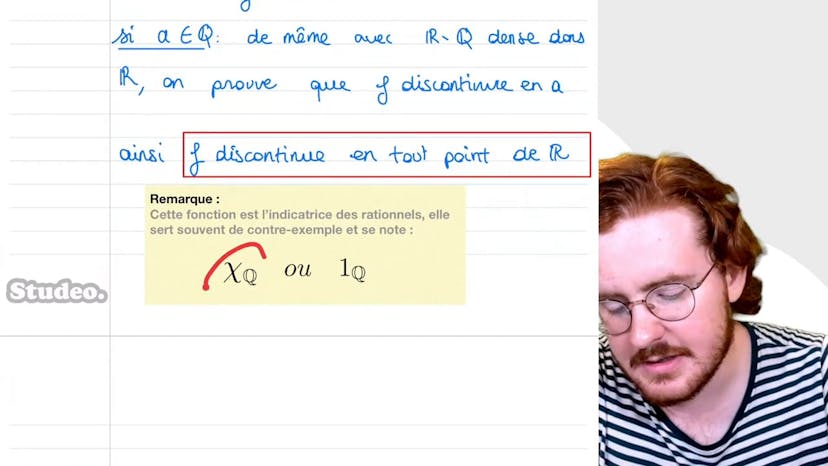
Indicatrice de Q
La fonction f de r dans R est définie par 1 si x est rationnel et 0 si x n'est pas rationnel. Il est montré que f est discontinue en tout point en utilisant la caractérisation séquentielle de la continuité. On prend un point a dans R et on montre qu'il existe une suite de réels qui tend vers a et dont la limite de f de ces réels n'est pas égale à f de a. Si a est irrationnel, on utilise le fait que R privé de q est dense dans R pour montrer la discontinuité. Cette fonction, l'indicatrice des irrationnels, est simple et sert souvent de contre-exemple sur la continuité.


