 Tous les sujets
Tous les sujets Maths
Maths Physique-Chimie
Physique-Chimie Corrigés de BAC
Corrigés de BAC Révisions Maths lycée
Révisions Maths lycée Prépa Examens
Prépa Examens
Terminale
Première
Seconde
MPSI/PCSI
2BAC SM Maroc
 Tous les sujets
Tous les sujets Maths
Maths Physique-Chimie
Physique-Chimie Corrigés de BAC
Corrigés de BAC Révisions Maths lycée
Révisions Maths lycée Prépa Examens
Prépa Examens
Physique-Chimie
Physique
MPSI/PCSI

Volume dans une seringue
Dans cette vidéo, nous abordons le chapitre des fondements de la thermodynamique. Nous commençons par examiner le cas d'une seringue dans laquelle nous comprimons l'air avec un piston. Au départ, la pression est égale à la pression atmosphérique, soit 1 bar. L'air est considéré comme un gaz parfait à température constante. Le problème consiste à déterminer la pression finale lorsque le volume est réduit de 90%.
Pour résoudre ce problème, nous devons choisir le système sur lequel appliquer les théorèmes de la thermodynamique. Dans ce cas, le système est l'air à l'intérieur de la seringue, avec une pression initiale de V1, un volume de V1, une température de T, et une quantité de matière Na. Nous pouvons utiliser l'équation d'un gaz parfait, P1V1 = NaRT, pour lier ces variables d'état.
En réduisant le volume de 90%, nous posons un défi pour déterminer les nouvelles variables d'état, P2, V2, T et Na. Comme la transformation est à température constante et qu'il n'y a pas de fuite d'air, T et Na restent les mêmes que dans l'état initial. En utilisant de nouveau l'équation d'état du gaz parfait, P2V2 = NaRT, nous pouvons résoudre le problème.
En utilisant les deux équations d'état, nous trouvons que P2V2 = P1V1, et en supposant que V2 = 0,1V1, nous pouvons conclure que P2 = 10P1. En effectuant le calcul, nous obtenons une pression finale de 10 bars pour cette transformation.
Dans la deuxième question, nous cherchons à obtenir une pression de 2,5 bars. En utilisant à nouveau l'équation P2V2 = P1V1, nous trouvons que le rapport V2/V1 est égal à P1/P2. Nous pouvons alors déduire que pour obtenir une pression finale de 2,5 bars, le volume doit être réduit de 60%.
En concluant, nous pouvons constater que l'utilisation de l'équation d'état du gaz parfait nous permet de résoudre ces problèmes thermodynamiques. En fixant les valeurs de Na, R et T, nous pouvons observer que la pression varie inversement avec le volume. Cette méthodologie nous permet de résoudre ces problèmes plus facilement.
Merci d'avoir suivi cette vidéo et à bientôt !
Physique-Chimie
Physique
MPSI/PCSI

Pression de pneus
Bonjour à tous ! Aujourd'hui, nous allons parler de la pression des pneus. La pression recommandée pour les roues avant d'une voiture est de 2,2 bars. Dans cet exercice, nous nous intéressons à la variation de pression en fonction de la température. Nous supposons que le volume des pneus ne change pas et qu'il n'y a aucune fuite d'air possible.
Nous devons déterminer l'indication du manomètre lorsqu'il fait 30 degrés. Pour cela, nous utilisons l'équation d'état d'un gaz parfait, qui relie la pression, le volume, la température et la quantité de matière. Nous avons P1V = NAR T1. En isolant P1 / T1, nous obtenons P1 / T1 = NA R / V.
Ensuite, nous déclarons un nouvel état final, avec une pression P2, un volume V, une température T2 et une quantité de matière NA. En utilisant à nouveau l'équation d'état des gaz parfaits, nous avons P2V = NAR T2. En isolant P2 / T2, nous obtenons P2 / T2 = P1 / T1.
Nous cherchons maintenant la pression finale, l'indication du manomètre, qui est donnée par P2 = P1 * T2 / T1. En effectuant les calculs, nous obtenons une pression P2 de 1,9 bars.
Ensuite, nous devons calculer la variation relative de pression due au changement de température. La variation relative de pression est donnée par (P2 - P1) / P1. En effectuant les calculs, nous obtenons une variation de 14%.
En conclusion, pour compenser la perte de pression due aux variations de température, il est conseillé de légèrement augmenter la pression des pneus entre chaque saison. Cela permet de maintenir une pression standard pour une conduite optimale.
Merci d'avoir suivi cet exercice sur la thermodynamique et à bientôt !
Physique-Chimie
Physique
MPSI/PCSI
Helium
Dans cette vidéo, Matisse de Studio parle de l'hélium contenu dans une bouteille de volume constant (10 litres) à une pression de 2,1 bar et une température de 300 Kelvin. Il utilise l'équation d'état des gaz parfaits pour calculer la masse d'hélium dans la bouteille, qui est de 3,4 g.
Il explique également comment calculer la densité particulière, qui est le nombre d'atomes par unité de volume, en utilisant l'équation d'état des gaz parfaits. La valeur obtenue est de 84 mol/m³.
Il aborde ensuite la vitesse quadratique moyenne des atomes, qui correspond à la norme de la vitesse moyenne des molécules dans une pièce. La vitesse quadratique moyenne est calculée à l'aide de l'énergie cinétique moyenne, qui est égale à 1,5 fois la masse molaire fois la vitesse quadratique moyenne au carré. En utilisant des valeurs numériques, la vitesse quadratique moyenne est de 789 m/s.
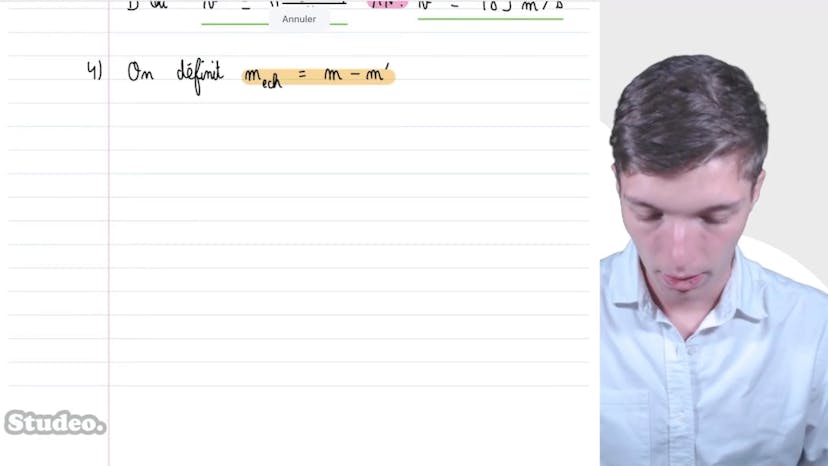
Ensuite, il analyse le cas où la pression passe à 1,4 bar et la température à 290 Kelvin après avoir ouvert la bouteille, ce qui entraîne une fuite de gaz. Il détermine la masse de gaz échappée en utilisant les nouvelles valeurs de pression et de température. La masse de gaz échappée est de 1,1 g d'hélium.
Enfin, il explique comment déterminer la température nécessaire pour que la bouteille retrouve sa pression d'origine. Il utilise l'équation des gaz parfaits avec la quantité de matière restante dans la bouteille. La température calculée est de 450 Kelvin.
En conclusion, Matisse souligne l'intérêt de cet exercice qui permet de comprendre les équations d'état des gaz parfaits et les variables importantes d'un système. Il encourage les spectateurs à revoir l'exercice de leur côté.
Physique-Chimie
Physique
MPSI/PCSI

Pot de confiture
Dans cette vidéo, Matisse de Studio parle de l'utilisation d'un pot de confiture. Il explique que pour remplir le pot, on verse de la confiture à une température de 105°C et à une pression atmosphérique de 1 bar. Le pot a un diamètre de 82 mm et on laisse un espace entre la confiture et le bord du pot. L'air emprisonné entre le couvercle et la confiture est considéré comme un gaz parfait à une température T1.
Le pot de confiture refroidit lentement jusqu'à atteindre une température de 20°C, et on souhaite déterminer la pression P2 à l'intérieur du pot à ce moment-là. Pour résoudre ce problème, Matisse applique la méthode classique de résolution thermodynamique. Il considère l'air à l'intérieur du pot comme le système et utilise l'équation d'état d'un gaz parfait (P1V = NAR T1) pour établir une relation entre la pression initiale (P1) et la température initiale (T1), et la pression finale (P2) et la température finale (T2). Il trouve finalement que la pression P2 est égale à 0,78 bar.
Ensuite, Matisse aborde la seconde question qui consiste à déterminer la résultante des forces de pression sur le couvercle du pot une fois qu'il est refroidi. Il explique que pour relier la pression aux forces de pression, il faut connaître la définition de la force de pression. La force de pression sur une surface est donnée par P fois la surface fois la normale sortante de la surface. En prenant en compte la pression intérieure et la pression extérieure, Matisse trouve que la force sur le couvercle est égale à la valeur absolue de la différence entre la pression intérieure et la pression extérieure, multipliée par la surface du couvercle. En effectuant les calculs numériques, il obtient une force de 1,2 10-3 N due à cette différence de pression.
Matisse explique que cela rendra plus difficile l'ouverture du pot, car la pression intérieure est inférieure à la pression extérieure. Il souligne que cela est dû aux forces de pression et à la sous-pression à l'intérieur du pot. Ces forces peuvent rendre encore plus difficile l'ouverture si le pot est sous vide. Il conclut en encourageant les spectateurs à comprendre pourquoi il est plus difficile d'ouvrir un pot en se basant sur la formule PxS (force de pression = pression fois surface) et en faisant des schémas pour mieux visualiser les concepts.
En résumé, cette vidéo explique comment remplir un pot de confiture, comment calculer la pression à l'intérieur du pot une fois qu'il est refroidi, et comment les forces de pression affectent l'ouverture du couvercle du pot.
Physique-Chimie
Physique
MPSI/PCSI
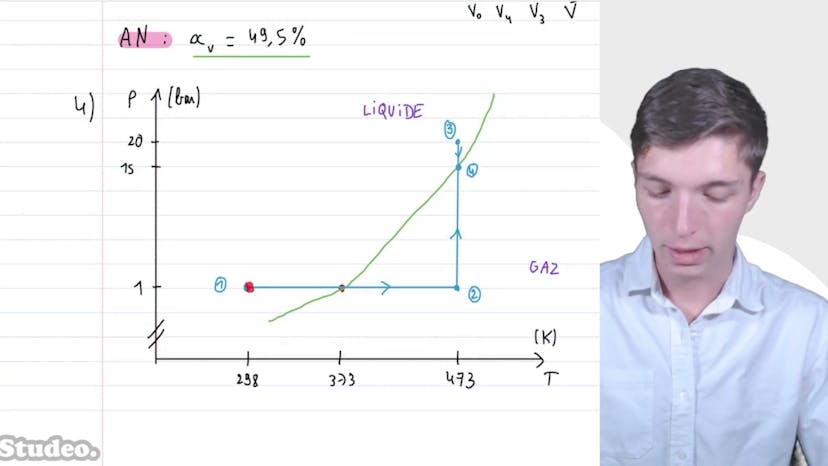
Diagramme (P,T)
Dans cette vidéo, nous étudions le diagramme pression-température de l'eau. Nous considérons une masse de 900 g d'eau à la température T1 de 298 Kelvin et à la pression de 1 bar. L'eau subit ensuite un chauffage à pression constante jusqu'à la température T2 de 473 Kelvin, puis une compression à température constante jusqu'à un volume de 100 litres, et enfin une détente à température constante jusqu'à un état d'équilibre liquide-vapeur de volume V4 de 50 litres. Nous tenons compte de la pression à vapeur saturante pour deux températures différentes, de la masse molaire de l'eau et de la constante des gaz parfaits.
Dans l'état 1, nous n'avons pas la pression de vapeur saturante, mais la pression correspond presque à la pression de vapeur saturante pour 373 Kelvin. Cela indique que nous sommes dans un état liquide à 298 Kelvin et dans un état gazeux à 473 Kelvin.
Pour l'état 2, qui correspond à l'état gazeux, nous pouvons utiliser l'équation d'état des gaz parfaits pour déterminer sa pression. En appliquant cette équation avec une masse de 900 grammes et la masse molaire de l'eau donnée, nous trouvons une pression de 20 bars. Nous pouvons alors comparer cette pression à la pression de vapeur saturante et conclure que l'état est liquide.
Pour déterminer le titre en vapeur d'eau dans l'état 4, qui est un mélange liquide-gaz, nous utilisons le théorème des moments. En appliquant ce théorème, nous trouvons un titre en vapeur de 49,5%.
Enfin, nous représentons les différentes transformations dans un diagramme pression-température, en passant d'une pression de 1 bar à 298 Kelvin à une pression de 20 bars à 473 Kelvin, avant de revenir sur la courbe de saturation pour le mélange liquide-gaz.
En résumé, cette vidéo explore différentes transformations de l'eau dans un diagramme pression-température. Elle aborde des concepts tels que la pression de vapeur saturante, l'équation d'état des gaz parfaits, le titre en vapeur d'eau et le théorème des moments. N'hésitez pas à revoir cet exercice pour mieux comprendre ces concepts. Merci de nous avoir suivi et à bientôt !
Physique-Chimie
Physique
MPSI/PCSI

Gaz parfait et piston
Dans cette vidéo, Matisse de Studio aborde un exercice sur le gaz parfait et le piston. Il explique que cet exercice est très classique et revient souvent dans les exercices de col ou en devoirs surveillés, donc il est important de le maîtriser.
L'exercice traite d'une quantité de matière N de gaz parfait enfermée dans une enceinte de surface S. Le piston qui ferme l'enceinte est supposé idéal, c'est-à-dire sans frottement avec l'enceinte. Le piston permet les transferts thermiques et lorsque le système atteint l'équilibre thermique avec l'extérieur, le gaz de l'enceinte est en équilibre thermique avec l'extérieur, qui est à une pression et une température constantes P0 et T0.
L'exercice comporte plusieurs états du système. Dans l'état 1, le système est au repos et a atteint l'équilibre thermique et mécanique. Ensuite, le gaz est chauffé à une température T supérieure à T0, ce qui constitue l'état 2. Une masse supplémentaire M est brusquement placée sur le piston, avant tout transfert thermique, ce qui correspond à l'état 3. Lorsque l'équilibre thermique est atteint, le système est dans l'état 4.
L'objectif de l'exercice est de déterminer les positions H1 à H4 du piston dans chaque état du système, c'est-à-dire la hauteur à laquelle se situe le piston dans chaque situation. Pour cela, Matisse propose de transformer cette notion de hauteur en une autre inconnue plus manipulable, à savoir le volume Vx de l'enceinte renfermée sous le piston. Comme la surface S de l'enceinte est constante, cela permet de déterminer plus facilement les différentes positions.
Pour déterminer le volume V1 dans l'état 1, Matisse établit l'équation d'état des gaz parfaits et montre que V1 est égal à NRT0 divisé par P1S plus Mg. Il explique qu'il faut déterminer P1, qui n'est pas directement donné dans l'énoncé, en utilisant le fait que le piston est à l'équilibre mécanique. Ainsi, il peut établir que P1 est égal à P0 plus Mg divisé par S.
Dans l'état 2, où le gaz est chauffé à une température supérieure, Matisse utilise le raisonnement précédent en changeant simplement la température, ce qui lui permet de déterminer que H2 est égal à nRT divisé par P0S plus Mg.
Dans l'état 3, où une masse supplémentaire est ajoutée brusquement sur le piston, Matisse explique qu'il n'y a pas d'impact sur les variables d'état du système thermique, mais que le bilan des forces appliquées sur le piston doit être ajusté en prenant en compte cette masse supplémentaire. Il conclut que la hauteur H3 est égale à H2.
Enfin, dans l'état 4 où l'équilibre thermique est atteint, Matisse montre que la situation est similaire à l'état 2, mais avec la température T0 et la masse effective de petit M plus grand M. Il obtient ainsi que H4 est égal à nRT0 divisé par P0S plus petit M plus grand M fois g.
Matisse souligne l'importance de comprendre la démarche globale de l'exercice et de repérer où chaque variation du système va changer une partie du raisonnement. Il encourage également à justifier chaque étape du raisonnement.
En conclusion, Matisse espère que son explication de cet exercice classique sur le gaz parfait et le piston a été claire et remercie les spectateurs de l'avoir suivi.
Physique-Chimie
Physique
MPSI/PCSI

Van der Waals
Dans cette vidéo, on découvre que l'équation d'état des gaz parfaits, notre équation préférée dans ce chapitre, est en fait un cas particulier d'une équation plus générale, l'équation de Van der Waals. Cette équation relie la pression, le volume et la température d'un fluide à l'aide de deux constantes positives, A et B, qui caractérisent le fluide. Pour une mole de gaz, l'équation devient P + A/V^2(V-B) = RT.
Il est possible de généraliser cette équation de Van der Waals pour N moles de fluide en prenant en compte le comportement des variables (pression, volume et température) lors du passage d'un système d'une mole à un système de N moles. La pression est une variable intensive, ce qui signifie qu'elle conserve sa valeur lorsqu'on combine deux sous-systèmes indépendants. La température est également une variable intensive. En revanche, le volume est une variable extensive, ce qui signifie qu'il augmente proportionnellement au nombre de moles de gaz.
En remplaçant V par V' = nV, où n est le nombre de moles de gaz, dans l'équation de Van der Waals, on obtient une version de l'équation pour un système constitué de N moles. En multipliant l'équation initiale par n, on retrouve V' dans l'équation.
En posant A = 0, on étudie l'influence de B, appelé covolume, qui représente l'effet de répulsion à courte distance entre les molécules. Pour l'hydrogène, on donne une estimation approximative de B en se basant sur la distance de liaison entre deux atomes d'hydrogène.
En posant B = 0, on étudie l'influence de A, qui représente l'effet attractif à courte distance entre les atomes. A a un effet opposé à B, avec un signe positif.
Le terme correctif de la pression dans l'équation de Van der Waals est une fonction décroissante du volume. Cela s'explique par le fait que plus le volume est important, moins l'effet attractif entre les atomes est intense. L'effet attractif perd en intensité lorsque les atomes sont éloignés les uns des autres, ce qui est pénalisé en divisant par V².
En conclusion, cet exercice permet de manipuler et d'analyser l'équation de Van der Waals, en comprenant ses différentes constantes et leurs effets sur la pression, le volume et la température des fluides.
Physique-Chimie
Physique
MPSI/PCSI

Double compartiment
Dans cette vidéo, Mathilis examine une enceinte à double compartiment contenant de la vapeur d'eau. L'enceinte a un volume de 10 litres et est dilaterme. Un piston de masse M et de surface S sépare les deux compartiments, avec 1,0 mol d'eau dans le compartiment supérieur et 0,10 mol d'air dans le compartiment inférieur. On considère que la vapeur d'eau et l'air sont des gaz parfaits. Pour déterminer la fraction molaire de vapeur d'eau, on doit trouver la quantité de matière de vapeur dans l'enceinte. Cela peut être trouvé en utilisant l'équation d'état des gaz parfaits, en utilisant la pression, le volume et la température. La pression est fixée à la pression de vapeur saturante à 100°C, qui est de 1 bar. Le volume est déterminé en utilisant le théorème fondamental de la statique et l'équation des gaz parfaits. En utilisant ces informations, on trouve que la fraction molaire de vapeur d'eau est de 27%. Il est également noté qu'une hypothèse a été faite au départ selon laquelle le volume du liquide est négligeable par rapport au volume du gaz, ce qui est justifié par le rapport de 1:2000 entre les volumes du gaz et du liquide. En conclusion, il est important de prendre son temps pour comprendre la problématique et de mettre en place une démarche appropriée pour résoudre ce type d'exercice en thermodynamique.
Physique-Chimie
Physique
MPSI/PCSI

Libre parcourt moyen
Dans cette vidéo, nous abordons la notion de libre parcours moyen, qui concerne la réalité microscopique des molécules. Le libre parcours moyen désigne la distance moyenne qu'une molécule parcourt avant de rencontrer une autre molécule. Pour le dioxygène à pression atmosphérique et à température ambiante, le libre parcours moyen est d'environ 100 nanomètres.
Pour comprendre le libre parcours moyen, nous considérons les molécules comme des sphères indéformables de diamètre d. Une molécule en mouvement entre en collision avec une autre molécule si le centre de la molécule en mouvement se situe à une distance inférieure à d de la trajectoire de la molécule fixe. On peut délimiter un cylindre de base πd² de hauteur L, où L représente le libre parcours moyen.
Nous pouvons définir le libre parcours moyen, L, comme la distance moyenne parcourue par une molécule avant de rencontrer une autre molécule dans ce cylindre. La hauteur limite à laquelle une molécule peut être placée sans entrer en collision est d.
Le libre parcours moyen, L, peut être exprimé en fonction du diamètre des molécules, d, et du nombre de particules par unité de volume, N. En utilisant le nombre d'Avogadro, Na, la constante de Boltzmann, KB, la pression atmosphérique P0 et la température T, nous pouvons obtenir une formule : L = 1/(Na * π * d² * N*).
Pour évaluer la taille des molécules dans le modèle du gaz parfait, nous utilisons la formule précédente et l'équation d'état du gaz parfait (P0 = N * KB * T / V) pour exprimer N en fonction de P0, T et d'autres constantes. Enfin, nous évaluons la taille D des molécules dans le modèle du gaz parfait en utilisant les valeurs numériques correspondantes et obtenons D = 0,36 nanomètre.
En commentant la valeur de D obtenue (0,36 nanomètre) par rapport à la taille d'une molécule de dioxygène (0,29 nanomètre), nous concluons que le modèle du gaz parfait et du libre parcours moyen peuvent décrire assez précisément les molécules de dioxygène. Cependant, il faudrait étudier d'autres molécules pour savoir si cette loi se généralise.


