 Tous les sujets
Tous les sujets Maths
Maths Physique-Chimie
Physique-Chimie Corrigés de BAC
Corrigés de BAC Révisions Maths lycée
Révisions Maths lycée- Analyse Terminale
- Géométrie Terminale
- Arithmétique Maths expertes
- Complexes Maths expertes
MPSI/PCSI Prépa Examens
Prépa Examens
Terminale
Première
Seconde
MPSI/PCSI
2BAC SM Maroc
 Tous les sujets
Tous les sujets Maths
Maths Physique-Chimie
Physique-Chimie Corrigés de BAC
Corrigés de BAC Révisions Maths lycée
Révisions Maths lycée- Analyse Terminale
- Géométrie Terminale
- Arithmétique Maths expertes
- Complexes Maths expertes
MPSI/PCSI Prépa Examens
Prépa Examens
Révisions Maths lycée
Probas Terminale
MPSI/PCSI

Utiliser un arbre pondéré
Dans cette vidéo, nous étudions les probabilités d'événements en utilisant un arbre pondéré. Nous avons des informations sur les habitudes de Naomi pour se rendre au lycée : si le temps est beau, elle prend le vélo 8 fois sur 10, et si le temps est moche, elle prend le vélo 5 fois sur 10. De plus, il y a 75% de journées ensoleillées dans sa ville. Nous voulons déterminer la probabilité de l'événement "ensoleillé et prendre le vélo" (E inter V) et la probabilité de prendre le vélo (V).
Nous commençons par construire un arbre pondéré avec les deux possibilités pour le temps (ensoleillé ou non) et les deux possibilités pour le moyen de transport (vélo ou autre). En utilisant les informations données, nous déterminons les probabilités associées à chaque nœud de l'arbre.
Ensuite, nous calculons la probabilité de l'événement "ensoleillé et prendre le vélo" en utilisant la formule P de E inter V = P de E x P de V sachant E. Nous trouvons que la probabilité est de 0,6, soit 60%.
Enfin, nous calculons la probabilité de prendre le vélo en utilisant la formule des probabilités totales en considérant les chemins de l'arbre où Naomi prend le vélo. Nous obtenons une probabilité de 72,5%.
C'est une méthode classique pour calculer les probabilités à l'aide d'un arbre pondéré.
Révisions Maths lycée
Probas Terminale
MPSI/PCSI
Représenter un schéma de Bernoulli
Dans ce cours, nous étudions le schéma de Bernoulli, qui représente une expérience répétée ayant deux résultats possibles : réussite ou échec. Dans cet exemple, Gloria remarque que lorsqu'un client entre dans sa librairie, il y a une probabilité de 67% qu'il achète un livre. Nous devons déterminer s'il s'agit d'un schéma de Bernoulli.
Pour justifier cela, nous devons vérifier si les clients sont indépendants les uns des autres et si leur choix d'achat ne dépend pas des clients précédents. Dans notre cas, les clients sont indépendants et leur choix n'est pas influencé par les autres. Donc, il s'agit bien d'un schéma de Bernoulli avec un nombre d'expériences (clients) n égal à 4 et une probabilité de succès (achat de livre) p égale à 0,67.
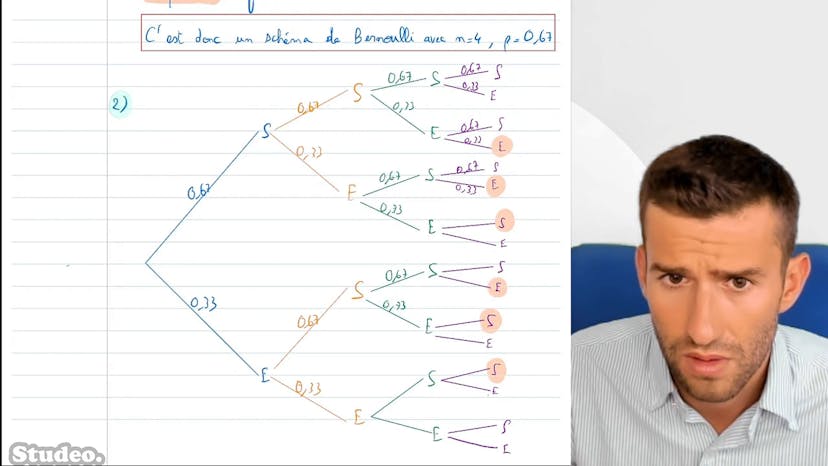
Ensuite, nous devons construire un arbre pour représenter tous les chemins possibles. Chaque nœud de l'arbre représente soit un succès (achat de livre) soit un échec (pas d'achat), avec une probabilité de succès de 67% et une probabilité d'échec de 33% à chaque nœud. Comme nous répétons l'expérience quatre fois, nous avons beaucoup de chemins possibles, mais grâce à l'arbre, nous pouvons les représenter tous.
Nous nous intéressons ensuite au cas où il y a exactement deux succès (deux achats). Nous pouvons utiliser une méthode manuelle pour compter tous les chemins qui correspondent à cette condition en utilisant l'arbre. Dans ce cas, il y a six chemins possibles correspondant à deux succès. En calculant la probabilité de chaque chemin (0,67² x 0,33²) et en les multipliant par le nombre de chemins (6), nous obtenons une probabilité de 29% pour avoir exactement deux personnes qui achètent des livres.
Cette méthode peut être généralisée avec la formule de la loi binomiale, ce qui nous donnerait une approche plus systématique pour calculer les probabilités. Cependant, dans cet exemple, l'arbre nous permet également d'obtenir le résultat souhaité.
Révisions Maths lycée
Probas Terminale
BCPST

Utiliser un arbre pondéré
Dans ce cours, nous utilisons un arbre pondéré pour calculer des probabilités d'événements. Nous savons que Naomi se rendra au lycée en vélo ou en bus. Lorsqu'il fait beau, elle prend le vélo 8 fois sur 10, et lorsqu'il fait moche, elle prend le vélo 5 fois sur 10. De plus, il y a 75% de journées ensoleillées dans la ville où elle habite.
Nous voulons déterminer les probabilités de l'événement "E inter V" et de l'événement "V". Pour cela, nous utilisons un arbre pondéré pour représenter les différentes probabilités. Nous complétons l'arbre avec les probabilités données, et nous vérifions que la somme des probabilités sur chaque branche est égale à 1.
Ensuite, nous calculons la probabilité de l'événement "E inter V" en utilisant la formule P(E inter V) = P(E) * P(V|E). Nous trouvons que la probabilité de "E inter V" est de 0.6, ce qui signifie qu'il y a 60% de chance qu'il fasse beau et que Naomi prenne le vélo.
Enfin, nous utilisons la formule des probabilités totales pour calculer la probabilité de l'événement "V". Nous trouvons que la probabilité de "V" est de 72.5%, ce qui signifie qu'il y a 72.5% de chance que Naomi prenne le vélo.
En résumé, nous utilisons un arbre pondéré pour calculer les probabilités des événements. Nous trouvons qu'il y a 60% de chance que Naomi prenne le vélo lorsque le temps est beau, et qu'il y a 72.5% de chance qu'elle prenne le vélo en général.
Révisions Maths lycée
Probas Terminale
BCPST

Représenter un schéma de Bernoulli
Dans ce cours, nous examinons le premier schéma de Bernoulli, qui concerne les achats de livres dans une librairie. La probabilité qu'un client achète un livre est de 67%. Nous avons quatre clients indépendants, et nous souhaitons déterminer la probabilité que deux d'entre eux achètent un livre.
Pour justifier que nous avons un schéma de Bernoulli, nous constatons qu'il s'agit d'une répétition de la même expérience avec deux résultats possibles: achat ou non achat. De plus, chaque client est indépendant et son choix n'est pas influencé par les clients précédents. Nous avons donc un schéma de Bernoulli avec n = 4 et p = 0,67, où le succès est défini comme l'achat d'un livre.
Ensuite, nous construisons un arbre pour représenter tous les cas possibles. Chaque nœud de l'arbre représente soit un succès (S), soit un échec (E), avec une probabilité de succès de 67% et une probabilité d'échec de 33%. Au total, cela nous donne beaucoup de possibilités, mais nous pouvons les représenter toutes sur l'arbre.
Ensuite, nous nous intéressons aux cas où exactement deux clients achètent un livre. Nous utilisons une méthode manuelle pour identifier tous les chemins de l'arbre correspondant à cette situation. Nous trouvons six chemins qui répondent à cette condition. En multipliant les probabilités de succès (0,67 au carré) et les probabilités d'échec (0,33 au carré) pour chaque chemin, et en multipliant le tout par six (le nombre de possibilités), nous obtenons une probabilité de 29% que deux clients achètent un livre.
Cette méthode peut être généralisée avec la formule de la loi binomiale, mais l'arbre nous permet également de trouver le résultat.
Révisions Maths lycée
Probas Terminale
ECG

Utiliser un arbre pondéré
Pour calculer les probabilités des événements dans cet exercice, nous utilisons un arbre pondéré. Nous avons des informations sur les probabilités et nous souhaitons en déduire d'autres.
Nous savons que Naomi se rendra au lycée en vélo ou en bus. Lorsqu'il fait beau, elle prend le vélo 8 fois sur 10, et lorsqu'il fait moche, elle prend le vélo 5 fois sur 10. De plus, dans sa ville, il y a 75% de journées ensoleillées.
Nous prenons une journée au hasard où nous ne savons pas s'il fait beau ou non. Nous voulons déterminer la probabilité que l'événement E et l'événement V se produisent, ainsi que la probabilité que V se produise sachant que E se produit.
Nous utilisons un arbre pondéré pour représenter les probabilités. Nous écrivons les probabilités associées à chaque nœud de l'arbre. Par exemple, la probabilité qu'il fasse beau est de 0.75 et la probabilité qu'il ne fasse pas beau est de 0.25.
Ensuite, nous utilisons les informations pour remplir l'arbre pondéré. Par exemple, sachant qu'il fait beau, la probabilité que Naomi prenne le vélo est de 0.8, donc la probabilité qu'elle ne prenne pas le vélo est de 0.2. De la même manière, si le temps est mauvais, la probabilité qu'elle prenne le vélo est de 0.5 et la probabilité qu'elle prenne le bus est également de 0.5.
Nous vérifions que la somme des probabilités pour chaque branche de l'arbre est toujours égale à 1.
Maintenant, nous pouvons calculer les probabilités des événements. La probabilité que les événements E et V se produisent simultanément est calculée en utilisant la formule P(E ∩ V) = P(E) * P(V|E). Dans notre cas, cela donne 0.75 * 0.8 = 0.6, donc il y a 60% de chances que Naomi prenne le vélo s'il fait beau.
Ensuite, nous voulons calculer la probabilité de l'événement V, c'est-à-dire la probabilité que Naomi prenne le vélo. Pour cela, nous utilisons la formule des probabilités totales, qui est P(V) = P(E) * P(V|E) + P(E') * P(V|E'). Dans notre cas, cela donne 0.75 * 0.8 + 0.25 * 0.5 = 0.725, donc il y a 72,5% de chances que Naomi prenne le vélo.
Ceci résume les calculs de probabilités effectués à l'aide d'un arbre pondéré.
Révisions Maths lycée
Probas Terminale
ECG

Représenter un schéma de Bernoulli
Dans ce cours, nous abordons le premier schéma de Bernoulli dans le contexte d'une librairie. Lorsqu'un client entre dans la librairie, la probabilité qu'il achète un livre est de 67%. Cette expérience est indépendante pour chaque client, ce qui en fait un schéma de Bernoulli avec n égal à 4 et p égal à 0,67.
Pour justifier que nous avons un schéma de Bernoulli, nous devons avoir une répétition de la même expérience avec deux résultats possibles (achat ou non-achat) et chaque client étant indépendant des précédents. Dans notre cas, les clients qui entrent dans la librairie soit achètent un livre, soit n'en achètent pas, ce qui correspond bien à un schéma de Bernoulli.
Ensuite, nous devons construire un arbre pour représenter toutes les possibilités. Bien que long, cela nous permet de visualiser toutes les issues possibles lorsque nous répétons cette expérience quatre fois. Chaque branche représente soit un succès (achat d'un livre), soit un échec (non-achat), avec une probabilité de succès de 67% et une probabilité d'échec de 33%.
En utilisant cet arbre, nous pouvons identifier tous les chemins où il y a exactement deux succès (deux achats). Après les avoir comptés, nous obtenons six chemins possibles. Chaque chemin a la même probabilité de se produire, car nous avons deux fois 0,67 et deux fois 0,33 dans chaque chemin. Ainsi, la probabilité d'obtenir deux personnes qui achètent des livres est de 29%.
Remarquons que cette méthode est un peu rudimentaire, mais elle peut être utile pour trouver des probabilités en lisant sur un arbre. Dans la prochaine méthode, nous utiliserons la formule de la loi binomiale pour généraliser le calcul de ces probabilités de manière plus systématique.


