Cours de Induction en Ligne par les Meilleurs Professeurs - Induction

Courant induit

Aucun résumé n'est disponible pour cette vidéo

Rotation de spire

Aucun résumé n'est disponible pour cette vidéo

Dans cette vidéo, nous examinons le mouvement d'un aimant droit de moment magnétique M, dont le pôle nord est orienté vers un circuit. Le circuit est composé d'une spire de rayon A, de centre O, d'axe OZ assimilable à une résistance R. L'aimant glisse le long de l'axe OZ à une vitesse constante V0. Le champ magnétique créé par l'aimant à une distance Z sur l'axe est donné par l'expression B = (-μ0M)/(2πZ^3). Le sens du courant d'intensité I est déterminé par l'orientation de la surface DS. Lorsque l'aimant recule, le flux du champ magnétique augmente, ce qui induit un champ magnétique induit dans le sens opposé pour lutter contre ce phénomène. Ainsi, la norme I est strictement négative. Pour déterminer la force électromotrice induite E, nous utilisons la loi de Faraday qui indique que E = -(dΦ/dt). En calculant le flux magnétique, on obtient Φ = -πA^3K/Z^3. En dérivant par rapport au temps, on trouve que E = -(3πA^2K)/(V0^3T^4). Pour déterminer la valeur de Z, on utilise la loi des mailles pour établir la relation entre I et E, soit I = E/R. Cela donne I = -(3πA^2K)/(RV0^3T^4). Lorsque l'aimant s'éloigne de la spire, le courant est négatif, ce qui est cohérent avec les résultats obtenus précédemment. L'aspire se comporte comme un aimant avec un moment magnétique dirigé vers le bas suivant l'axe EZ. Par conséquent, elle exerce une force d'attraction sur le véritable aimant. Si l'aimant est immobile mais proche de l'aspire, il n'y a pas de mouvement, donc pas de variation du flux magnétique, et donc pas de courant induit. Cet exercice nous montre comment étudier le comportement d'une spire en tant qu'aimant et prédire ses effets sur le déplacement d'un aimant réel.

Barre et ressort

Aucun résumé n'est disponible pour cette vidéo

Rails de Laplace

Aucun résumé n'est disponible pour cette vidéo

Rail de Laplace + ressort

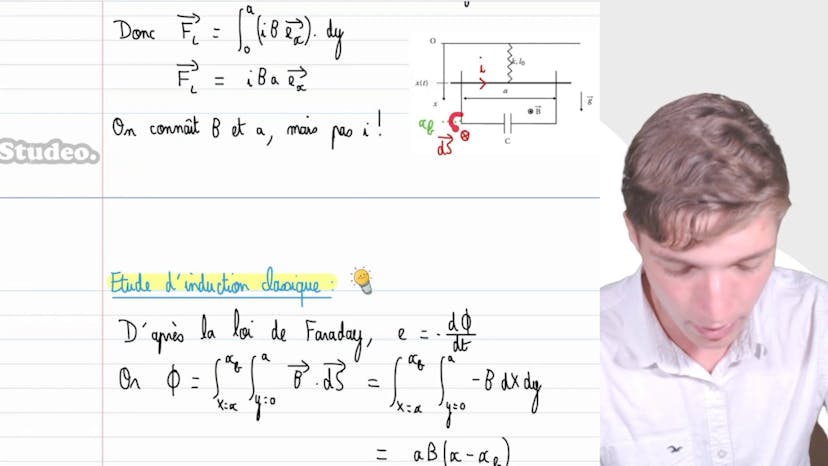
Bonjour à tous, dans cette vidéo nous étudions un dispositif de rails avec une barre attachée à un ressort. La barre a une longueur à vide L0, une constante de raideur k, une masse m, et une longueur a. Lorsque la barre est déplacée de la position d'équilibre x0 à l'instant t = 0, il y a plusieurs phénomènes qui se produisent. Tout d'abord, le ressort va déplacer la barre pour la ramener à sa position d'équilibre. Cependant, en raison du champ magnétique dans lequel se trouve le dispositif, le mouvement de la barre va créer une variation de flux magnétique à travers le circuit, ce qui génère une force de freinage qui ralentit la progression de la barre. De plus, une partie du courant induit va être dissipée par effet joule dans la résistance du circuit. Finalement, le système se stabilisera à la position d'équilibre. Le sens du courant induit dépend du sens du déplacement de la barre. Si la barre se déplace vers la droite, le courant induit va circuler dans le sens opposé. Si la barre se déplace vers la gauche, le courant induit circulera dans le sens de déplacement de la barre. En résolvant les équations électriques et mécaniques du système, nous obtenons l'équation du mouvement x'' + (1/tau)x' + (ω0^2)x = 0, avec tau = MR/AB^2 et ω0^2 = k/m. Pour avoir un régime pseudo-périodique, la résistance R doit satisfaire R < 2AB^2(ω0^2/m)^3. En résolvant cette équation, nous obtenons l'expression de x(t) =

Freinage par induction

Aucun résumé n'est disponible pour cette vidéo

Carte magnétique

Aujourd'hui, nous allons parler des cartes de champs magnétiques. Pour construire ces cartes, nous utilisons des champs électriques plutôt que des aimants. Cependant, cela ne nous apporte pas beaucoup d'informations. L'objectif principal est de trouver les positions des sources de courant et leur direction. Un champ magnétique est créé par des courants. Nous pouvons déterminer la direction du champ en observant la direction des flèches sur les cartes. Les lignes de champs ont tendance à s'enrouler autour des sources de courant, notées par des points noirs sur les cartes. Pour déterminer le sens du courant, nous utilisons la règle de la main droite. Si nous tournons notre main dans le sens des flèches, le champ a tendance à se diriger vers nous. Si nous tournons dans le sens contraire des flèches, le champ a tendance à s'éloigner. Ainsi, nous pouvons déterminer le sens du courant en fonction de la direction de rotation. Ensuite, nous abordons les zones de champ fort et de champ faible. Pour savoir si un champ est fort ou faible, nous observons si les lignes de champs se resserrent ou s'espacent. Les zones où les lignes se resserrent indiquent un champ fort, tandis que les zones où les lignes s'espacent indiquent un champ faible. En ce qui concerne le champ uniforme, cela signifie que les lignes de champs sont régulièrement espacées. Sur les cartes présentées, il n'est pas clair si des zones uniformes existent, car les lignes semblent se resserrer ou s'espacer partout. Dans l'idéal, des lignes uniformément espacées indiqueraient une zone de champ uniforme. J'espère que ces explications vous ont été utiles. À bientôt pour la suite sur la phénoménologie du champ magnétique.

Champ créé par une spire

Dans cette transcription vidéo, on aborde le thème du champ magnétique créé par une spire circulaire parcourue par un courant d'intensité I. On nous demande de calculer ce champ magnétique sur l'axe Z. La formule donnée est BM = mu0I/2R sin(3α)Z. Tout d'abord, on nous demande de déterminer le signe de l'équation en utilisant la règle de la main droite ou du tire-bouchon pour déterminer le sens du champ magnétique au point M. Pour cela, il faut observer le sens du courant I et appliquer la règle appropriée. Ensuite, on nous demande de déterminer le moment magnétique de la spire, qui est défini comme étant le produit de l'intensité du courant I et du vecteur surface de la spire S, qui suit également la règle de la main droite. Le résultat est M = -πR²Iez. Enfin, on nous demande d'exprimer le champ magnétique en fonction du moment magnétique M lorsque le point M est très éloigné de la spire (Z très grand devant R). Dans ce cas, on peut approximer sin(2α) par R/Z et obtenir la formule B = -μ0M/2πZ³. En résumé, ce cours aborde le calcul du champ magnétique d'une spire circulaire et donne les définitions du moment magnétique et des développements limités. Il souligne l'importance de la règle de la main droite pour déterminer la direction du champ magnétique et explique comment simplifier les calculs lorsqu'on a une grande différence de taille entre les dimensions impliquées.

Aimentation

Aujourd'hui, nous allons parler de l'aimantation et comment calculer le moment magnétique pour différents matériaux magnétiques. L'aimantation est définie comme le moment magnétique volumique et mesure en kiloampères par mètre (kA/m). Le moment magnétique se calcule en multipliant l'aimantation par le volume d'un aimant permanent. Par exemple, pour un aimant rond de NDFEB avec une épaisseur E et un rayon R, on peut calculer le moment magnétique en multipliant l'aimantation (3000 kA/m) par le volume (πR²E). Cela nous donne un moment magnétique d'environ 0,2 A*m². Comparé aux aimants permanents, il est également possible de créer des champs magnétiques en faisant passer un courant à travers une bobine ou une spire. Pour déterminer combien de spires seraient nécessaires pour atteindre le même moment magnétique qu'un aimant permanent, nous utilisons la formule M = NIS, où N est le nombre de spires, I est l'intensité du courant et S est la surface de la spire. En trouvant la valeur de N qui égale le moment magnétique de l'aimant permanent, on peut déterminer qu'il faudrait 30 000 spires avec le même rayon pour atteindre le même moment magnétique. En conclusion, l'aimantation est une mesure importante dans l'étude des matériaux magnétiques. Elle peut être utilisée pour calculer le moment magnétique d'un aimant permanent et comparer celui-ci avec le moment magnétique créé par une bobine ou une spire avec un courant passant à travers. (Note: l'aimantation a été donnée en kA/m et l'auteur a vérifié l'unité du moment magnétique et a utilisé des valeurs d'ordre de grandeur pour les calculs.)

Aimant en équilibre

Dans cet exercice, nous devons placer un aimant fin sur le sommet d'une pointe de telle manière qu'il reste en équilibre vertical. L'aimant est soumis à un champ magnétique uniforme et à la gravité. Pour résoudre cet exercice, nous utilisons le principe de la statique et faisons appel aux notions de mécanique des solides en rotation et de moment cinétique. Nous calculons d'abord les moments des forces exercées sur l'aimant : le moment du poids et le moment de la force magnétique. Le moment du poids est égal à dMg, où d est la distance entre le centre de gravité de l'aimant et l'axe delta. Ensuite, nous calculons le couple magnétique, qui est équivalent au moment de la force magnétique. Le couple magnétique est donné par mu vectoriel P, où mu est le moment magnétique de l'aimant. Pour obtenir l'équilibre, nous cherchons à ce que la somme des moments soit nulle. Cela nous permet de déterminer la distance à laquelle il faut placer la pointe du centre de gravité de l'aimant pour qu'il reste en équilibre vertical. Cette distance est égale à mu B sur Mg. En résumé, pour résoudre cet exercice, il est important de comprendre le théorème du moment cinétique et de calculer correctement les moments des forces et le couple magnétique. Ensuite, nous utilisons le théorème de la statique pour les solides en rotation. N'hésitez pas à poser vos questions si besoin.