Cours de Suites en Ligne par les Meilleurs Professeurs - Suites

Introduction à la récurrence

Ce cours vidéo explique la méthode de démonstration par récurrence, souvent utilisée dans le cadre des suites. Pour comprendre cette méthode, l'exemple classique de la somme des n premiers entiers consécutifs est utilisé.

Concept et rédaction

Dans cette vidéo, le professeur explique l'importance de la rédaction, de l'initialisation et des erreurs à ne pas faire lorsqu'on démontre une propriété par récurrence. Le principe général consiste à montrer que si une propriété est vraie pour un entier, elle est vraie pour l'entier suivant. Pour cela, on utilise une initialisation et une transmission de la propriété. Il est crucial de conclure la démonstration. Dans 90% des exercices, la propriété sera vraie pour n=0, mais dans 10% des cas, elle sera vraie pour un autre entier. Le professeur donne l'exemple d'une suite définie de manière récurrente. Enfin, il montre un exemple de démonstration de propriété pour illustrer la rédaction attendue.

Pourquoi l'initialisation ?

Dans ce cours, l'importance de la pitch net initiale est mise en avant, et un exemple est donné pour illustrer cela. Il est expliqué que certaines propriétés peuvent se transmettre même si elles sont fausses, comme l'exemple de P2N, qui n'est pas divisible par 3 mais qui peut être transmis d'un anti à l'autre dans une boucle. Cependant, pour trouver une initialisation pour cette propriété, il faut être complet et s'embêter à la faire à chaque fois, car il n'y aura jamais d'initialisation pour cette propriété. En somme, l'initialisation est importante et ne doit pas être négligée.

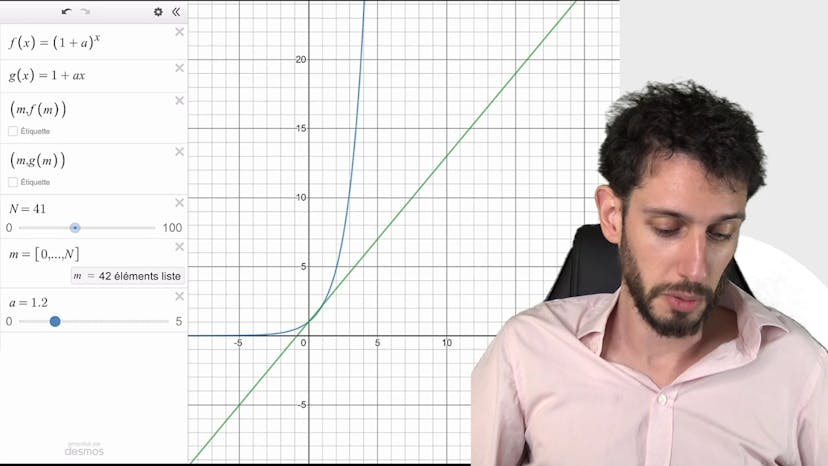
Inégalité de Bernoulli : visuel

Dans cette vidéo, l'inégalité de Bernoulli est expliquée visuellement. L'inégalité énonce que pour tout réel A positif et entier N, 1 + A^N est supérieur ou égal à 1 + NA. Cette inégalité est étudiée dans le contexte de la récurrence, car la démonstration par récurrence est simple. L'objectif de cette vidéo est de fournir une intuition graphique plutôt qu'une simple mémorisation de la formule. Les deux éléments de l'inégalité sont considérés comme des fonctions, la gauche étant une exponentielle et la droite une affine. En utilisant un graphique interactif, on peut observer la relation entre les deux fonctions pour différentes valeurs de A. On constate que l'exponentielle monte beaucoup plus rapidement que la fonction affine, ce qui explique l'inégalité de Bernoulli. Les points de la suite définie par F à partir de G sont également tracés, montrant que la suite F est toujours supérieure à la suite G pour les entiers positifs. La vidéo se termine en expliquant que la compréhension de cette inégalité de Bernoulli est essentielle pour les démonstrations et qu'elle est basée sur une intuition graphique facilement accessible.

Intro Suites et limites

Lors de cette vidéo sur les limites de suite, le professeur explique que les définitions formelles peuvent paraître moches et effrayantes, mais qu'elles sont nécessaires pour obtenir des prédictions précises. Il suggère de toujours se référer aux dessins qui accompagnent les formules, pour mieux les comprendre. À cet égard, les limites de suite ont des similitudes avec l'étude des dérivées, où les tables de dérivées classiques ont remplacé les calculs fastidieux de taux d'accroissement. Dans le cas des limites de suite, il y a des tableaux de limites classiques à connaître par cœur. Le cours est divisé en trois parties principales: la définition des limites en infini, en moins infini, et en un point L réel, la présentation des limites de référence et des opérations sur les limites, et enfin une section bonus sur les limites des suites géométriques. Les principales méthodes d'étude incluent l'application de la définition formelle dans les exercices, l'utilisation des limites de référence et des opérations pour prédire les limites, la résolution de cas plus compliqués, et un rappel sur la somme des termes d'une suite géométrique.

Intro Convergence

Les théorèmes de convergence sont utilisés pour analyser des suites mathématiques complexes qui peuvent sembler difficiles à comprendre. Les deux théorèmes principaux sont le théorème de comparaison et le théorème de gendarme, qui ont des applications spécifiques pour montrer que les suites convergent ou divergent. Les suites minorées, majorées et bornées sont également définies, ce qui conduit au théorème de convergence monotone, important pour les mathématiques de niveau avancé. Les méthodes comprennent la gestion de sinus de n, de moins-un puissance n, et les suites homographiques, qui tombent souvent dans les examens.

Récurrence et croissance

La démonstration par récurrence est une méthode importante à maîtriser en mathématiques. Pour prouver l'hérédité de la suite, qui est la partie la plus compliquée de cette démonstration, voici quelques astuces. Pour démontrer que la suite est strictement décroissante, on définit la propriété P2n, qui est vraie pour tout n. Pour l'initialisation, on commence par u0 et pour l'hérédité, on écrit l'hypothèse de récurrence et ce qu'on veut montrer, en veillant à être explicite. Pour montrer que un+2 est plus petit que un+1, on utilise l'hypothèse de récurrence en la composant avec une fonction affine f, qui est strictement croissante. Enfin, on montre l'hérédité rigoureusement. Il est important de ne pas confondre la valeur de la suite au rang n avec l'objet suite elle-même, en utilisant des parenthèses pour éviter toute ambiguïté.

Conjecture puis récurrence

Dans ce cours, on utilise la démonstration par récurrence pour calculer la somme des entiers de 1 à n, qui est égale à n*(n+1)/2. Il est important de connaître le résultat que l'on veut démontrer avant d'utiliser cette méthode. On pose la proposition P2n selon laquelle la somme des entiers naturels jusqu'à n est égale à n*(n+1)/2. On vérifie ensuite la propriété pour n=1, puis on utilise l'hypothèse de récurrence pour montrer que P2n+1 est aussi vrai. En factorisant par n+1, on démontre que pour tout n antinaturel non nul, la somme des entiers de 1 à n est égale à n*(n+1)/2.

Hérédité : comment démarrer ?

Dans ce cours de mathématiques, on nous montre comment utiliser la méthode de récurrence pour démontrer l'hérédité. Pour cela, on utilise deux cas possibles : soit on part de l'hypothèse de récurrence, soit on part de la propriété au rang Un+1. Ces deux méthodes sont possibles et il n'y a pas de méthode meilleure, tout dépend de l'exercice. Il est également important de faire le lien entre l'hypothèse de récurrence et ce que l'on veut démontrer. En utilisant un exemple simple, on montre que la méthode de récurrence permet de prouver que pour tout n, Un est strictement positif.

Limite avec A ou Ɛ

Dans ce cours, on explique la définition mathématique d'une limite en mathématiques. L'objectif est de trouver le plus petit entier n0 tel que, pour toutes les valeurs de la suite au-delà de ce rang, elles soient supérieures à un certain réel a. Cela signifie que même si le réel a est très grand, il existe un rang à partir duquel toutes les valeurs de la suite seront supérieures à a. Pour trouver n0, on résout une équation et utilise la partie entière du résultat pour s'assurer que n0 est un nombre entier. La définition complète de la limite est illustrée par un exemple de suite qui tend vers l'infini. Bien que les définitions formelles puissent sembler difficiles, elles sont importantes pour comprendre les limites en mathématiques.

Forme indéterminée 1 : factoriser par terme de plus haut degré

Dans ce cours, nous allons étudier les méthodes pour calculer des limites indéterminées. Nous commençons avec le cas des polynômes en n, où le terme de plus haut degré est le seul à compter. Nous le démontrons en factorisant par le terme de plus haut degré et en observant le comportement de la fraction obtenue. Si nous avons un terme de plus l'infini fois un coefficient, nous obtenons une limite qui tend vers plus l'infini. Ainsi, la factorisation par le terme de plus haut degré nous permet de déterminer le coefficient dominant qui va imposer la limite. Cette méthode fonctionne pour tous les polynômes.