Cours de Admission Polytechnique en Ligne par les Meilleurs Professeurs - Admission Polytechnique

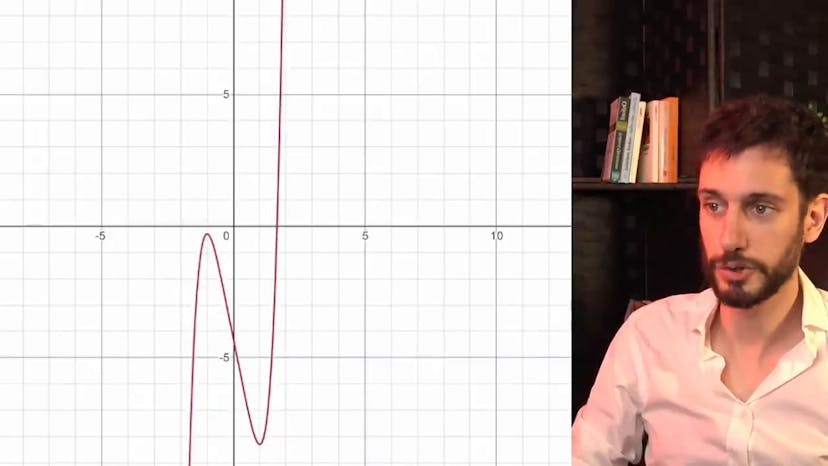
Solutions d'une équation de degré 5 !

Le cours aborde la résolution d'une équation de degré 5 qui consiste à trouver le nombre de solutions réelles en fonction d'un paramètre p. L'exercice nécessite une analyse approfondie de la fonction x^5 - 5x - p. Un graphe de la fonction est présenté pour illustrer les différentes valeurs de p et le nombre de solutions correspondant. En utilisant le théorème des valeurs intermédiaires, le professeur détermine différentes conditions pour le nombre de racines en fonction de la valeur de p. Il trouve qu'il y a une unique racine entre 1 et l'infini pour p>4, deux racines pour p=4, et trois racines pour -4<p<4. Pour p<-4, il y a à nouveau une unique racine. En résumé, l'ensemble des solutions de l'équation dépend de la valeur de p et peut être déterminé en analysant les différentes conditions. Le professeur encourage les étudiants à poser des questions et conclut en indiquant que d'autres exercices du même type seront présentés dans des vidéos futures.

Étude de fonction avec paramètre !

Dans cette vidéo, nous allons corriger un exercice de mathématiques portant sur une fonction avec un paramètre P. L'exercice peut sembler simple au premier abord, mais il est en réalité assez long, notamment à cause de détails et de questions auxiliaires. L'équation donnée est Exponentielle x égale 2 moins x puissance P, et nous devons prouver qu'il existe une seule solution positive à cette équation lorsque P est égal à 0. Nous pouvons exclure le cas P égal à 0 rapidement car cela donnerait 2 moins x puissance 0, qui est égal à 1, donc cela ne nécessite pas d'étude supplémentaire. Ensuite, nous devons montrer qu'il n'y a qu'une seule solution positive à l'équation pour P non nul, et nous devons également vérifier si des solutions négatives sont possibles. Pour répondre à ces questions, nous utilisons une méthode générale consistant à poser une fonction et à étudier ses propriétés, notamment ses dérivées. Nous utilisons également un théorème de valeur intermédiaire pour montrer l'existence de solutions. Dans le cas où P est impair, nous montrons que la fonction a une unique solution sur R+ (l'ensemble des nombres réels positifs). Dans le cas où P est pair, nous séparons l'étude de la fonction en deux parties : R+ et R-. Sur R+, nous montrons également qu'il y a une unique solution. Sur R-, nous utilisons les dérivées de la fonction pour montrer qu'il existe une valeur négative où la fonction s'annule. En conclusion, nous avons donc démontré qu'il existe une unique solution positive pour toute valeur de P, et des solutions négatives pour certaines valeurs de P. Malgré la complexité de l'exercice, il est possible de résoudre les questions en utilisant des méthodes standard telles que le calcul de dérivées et l'utilisation du théorème de valeur intermédiaire.

Développer des cubes

La vidéo est une transcription d'un cours sur la résolution d'un exercice lié au Bachelor de l'école polytechnique. Le cours explique comment simplifier et développer la formule de (A + B) au cube. Il rappelle d'abord la formule de base A cube + 3A carré B + 3A B carré + B cube, puis propose deux astuces pour retrouver les formules plus facilement. La première astuce consiste à remarquer que les puissances totales de chaque terme sont toujours égales à 3, et elles sont décroissantes pour A et croissantes pour B. La deuxième astuce est d'utiliser le triangle de Pascal pour trouver les coefficients devant chaque terme. En combinant ces deux astuces, on peut facilement trouver la formule pour n'importe quelle puissance de (A + B). Ensuite, le cours résout l'exercice en utilisant la formule (A + B) au cube et (X + A) au cube, puis en faisant la différence des deux. Finalement, il trouve que la différence est égale à 6X carré A + 2A cube. Le cours se conclut en rappelant que cette astuce peut être utile pour calculer n'importe quelle puissance d'une somme.

Une équation de complexes

Dans cette vidéo, l'exercice consiste à résoudre pour tout nombre complexe Z l'équation ZZ-bar-i. Le professeur rappelle qu'il est important de toujours réfléchir à des méthodes de calcul de base et d'optimisation pour résoudre les exercices plus rapidement. Le professeur suggère de chercher une simplification ou un argument géométrique pour faciliter la résolution de l'équation. Dans cet exercice, il remarque que ZZ-bar représente le carré du module de Z et suggère de considérer que l'équation représente l'ensemble des points d'un cercle. Cependant, cela ne permet pas de résoudre immédiatement l'équation. Le professeur propose donc une méthode plus brutale consistant à poser Z en utilisant la forme A+IB. Il explique qu'il préfère généralement éviter cette méthode brutale, mais estime qu'elle est plus efficace dans cet exercice particulier. Il développe mathématiquement l'équation avec cette méthode et trouve que cela mène à un polynôme pour lequel le discriminant est négatif, ce qui signifie qu'aucun nombre complexe ne satisfait l'équation. Il souligne l'importance de maîtriser ces petites questions simples lors des examens oraux et invite les spectateurs à consulter d'autres vidéos de sa chaîne où il résout d'autres exercices de difficulté variée. Il conclut en disant au revoir et en se donnant rendez-vous pour la prochaine vidéo.