Cours de Nombres et Calcul numérique en Ligne par les Meilleurs Professeurs - Nombres et Calcul numérique

Simplifier une racine

L'exercice consiste à écrire √263250 sous la forme a√b. Pour ce faire, il faut d'abord décomposer 236250 en facteurs premiers, en partant des plus petits jusqu'à obtenir 1. On compte ensuite le nombre de fois que chaque nombre premier apparaît, ce qui donne 2^1 x 5^4 x 3^3 x 7^1. Les propriétés des racines carrées et des puissances sont ensuite rappelées, notamment la propriété disant que la racine carrée d'un produit est égale au produit des racines carrées de chaque facteur. En utilisant cette propriété et en faisant apparaître les carrés, on obtient √263250 = 75√42.

Petite démo d'arithmétique

Dans cet exercice, on montre la transitivité de la divisibilité. Si un nombre divise un autre, mais est divisible par un autre nombre, que se passe-t-il pour les nombres des extrémités? On utilise le rappel selon lequel quand on a deux entiers A et B, A divise B s'il existe un K tel que B soit égal à K fois A. En utilisant cela, on traduit les informations données sous forme algébrique. On remplace D dans l'expression N = K x D par l'expression D = K' x D'. En substituant D par K' x D', on trouve que N est équal à K x K' x D'. On introduit un nouveau nombre positif ou négatif L, égal à K x K', montrant clairement que N est égal à L fois D', ce qui signifie, par la définition de la divisibilité, que D' divise N.

Décomposer en facteurs premiers

Dans cet exercice de décomposition en facteurs premiers, nous allons diviser successivement le nombre 182 952 par tous les nombres premiers. Nous commençons par les plus petits. Nous traçons une ligne pour séparer les nombres trouvés lors de la division et les diviseurs qui nous intéressent. Nous observons que 182 952 est un nombre pair, divisible par 2. Nous écrivons donc 2 x 91 476. Puis, nous divisons 91 476 par 2 pour obtenir 2 x 45 738. Enfin, nous divisons 45 738 par 2 pour obtenir 2 x 22 869. Le chiffre final de 22 869 ne nous permet pas de le diviser par 2, nous testons donc le prochain nombre premier, 3. Nous appliquons le critère de divisibilité par 3, et obtenons 3 x 7623. Nous testons à nouveau le nombre 7623, en appliquant à nouveau le critère de divisibilité par 3, pour obtenir 3 x 2541, puis 3 x 847. Nous testons ensuite si 847 est divisible par 7, en appliquant le critère de divisibilité par 7. Nous séparons le nombre en deux (84 et 7), puis additionnons le premier et le double du second (84 + 7 x 5 = 119). Nous répétons ce critère avec 11 et 9 (11 + 9 x 5 = 56), pour obtenir que 119 est divisible par 7, et donc que 847 est divisible par 7. Nous continuons ainsi la division jusqu'à obtenir que 182 952 est égal à 2 puissance 3 x 3 puissance 3 x 7 x 11 puissance 2, soit la décomposition en facteurs premiers de 182 952.

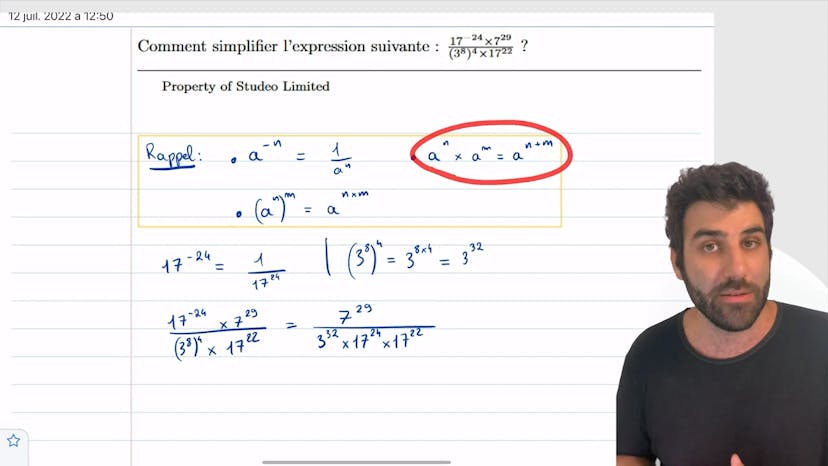
Simplifier des puissances

Dans cet exercice, on simplifie une fraction avec des puissances en utilisant 3 règles : a puissance moins n vaut 1 sur a puissance n, a puissance n fois a puissance m vaut a puissance n+m et a puissance n puissance m vaut a puissance n fois m. On applique ces règles pour réécrire 17 puissance moins 24 en 1 sur 17 puissance 24, simplifier 3 puissance 8 puissance 4 en 3 puissance 32 et regrouper les 17 sous une même puissance. On obtient ainsi la fraction simplifiée 7 puissance 29 sur 3 puissance 32 fois 17 puissance 46.