Cours de Vecteurs du Plan en Ligne par les Meilleurs Professeurs - Vecteurs du Plan

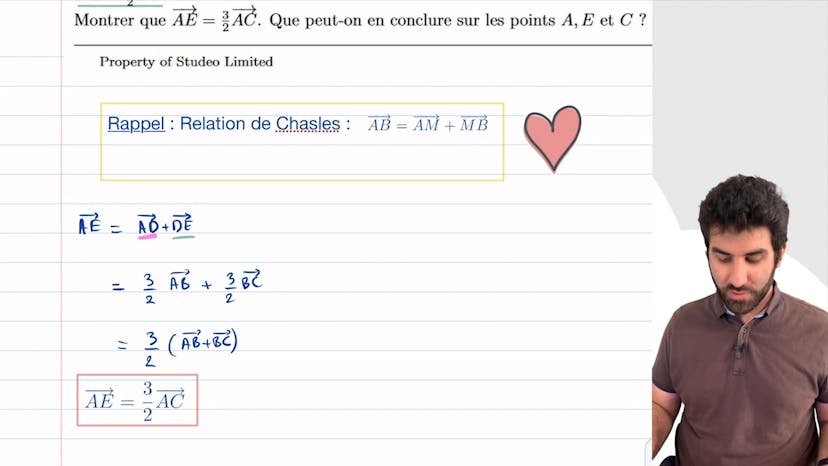
Relation de Chasles

Dans cet exo, on nous donne des relations de vecteurs et on nous demande de conclure sur les points A, E et C. Pour montrer qu'ils sont alignés, on utilise la relation de Schall qui dit qu'un vecteur AB peut être décomposé comme un vecteur AM plus MB pour n'importe quel point M. En utilisant cette relation, on écrit que AE est égal à 3,5 de AC, ce qui signifie que les vecteurs AE et AC sont collinéaires et donc alignés.

Vecteurs et alignement

Pour montrer que trois points sont alignés, on peut utiliser la méthode classique en utilisant des vecteurs. Trois points sont alignés si les vecteurs créés par ces points sont collinéaires. Deux vecteurs sont collinéaires s'il existe un coefficient de proportionnalité, k. On peut calculer les coordonnées de chaque vecteur en utilisant les formules xB-xA et yB-yA pour AB, et xC-xA et yC-yA pour AC. Ensuite, on peut observer que le vecteur AB est égal à moins 1 fois le vecteur AC, et donc AB et AC sont collinéaires. Cette propriété nous permet de conclure que les points ABC sont alignés.

Coordonnées d'un vecteur

Dans cet exercice, on cherche les coordonnées du point C pour que l'égalité entre les vecteurs AC et -2AB soit vérifiée. Pour cela, on utilise la formule des coordonnées d'un vecteur et la règle de calcul d'une multiplication entre un nombre et un vecteur. On calcule d'abord les coordonnées du vecteur AB, puis on multiplie chaque coordonnée par "-2" pour obtenir les coordonnées du vecteur -2AB. Ensuite, on calcule les coordonnées du vecteur AC en utilisant les coordonnées inconnues du point C. Enfin, pour que l'égalité soit vraie, on crée deux équations en égalant les coordonnées de chaque vecteur et on résout pour les coordonnées de C, qui sont finalement trouvées être 11 et -16.