 Tous les sujets
Tous les sujets Maths
Maths Physique-Chimie
Physique-Chimie Corrigés de BAC
Corrigés de BAC Révisions Maths lycée
Révisions Maths lycée Prépa Examens
Prépa Examens
Terminale
Première
Seconde
MPSI/PCSI
2BAC SM Maroc
 Tous les sujets
Tous les sujets Maths
Maths Physique-Chimie
Physique-Chimie Corrigés de BAC
Corrigés de BAC Révisions Maths lycée
Révisions Maths lycée Prépa Examens
Prépa Examens
Maths Spé
Probabilités
Terminale

Permutations : application
Dans ce cours, nous allons aborder la gestion des permutations. Une permutation peut être définie comme le nombre de façons de changer l'ordre d'une liste. Par exemple, si nous avons un tirage de loto, combien de possibilités avons-nous pour changer l'ordre de ce tirage une fois qu'il est fixé ?
Nous allons prendre comme exemple une conférence avec 12 scientifiques, dont 6 hommes et 6 femmes. Parmi eux, il y a 5 mathématiciens, 3 physiciens et 4 biologistes. Chaque corps de science a décidé d'utiliser une méthode différente pour se placer. Dans tous les cas, il y a 3 méthodes différentes.
La méthode des mathématiciens consiste à se placer au hasard. Dans ce cas, nous avons 12 personnes qui sont déjà fixées et nous cherchons à déterminer combien de façons de les positionner. Le nombre de permutations d'un ensemble à n éléments est donné par la formule n!. Dans notre cas, cela signifie que nous avons 12! façons de positionner ces scientifiques, ce qui correspond à environ 479 millions de possibilités.
Les physiciens, quant à eux, préfèrent rester ensemble. Donc nous devons d'abord les positionner, sachant qu'ils doivent rester ensemble. Ensuite, nous pouvons permuter les positions à l'intérieur de leur groupe. Une fois que nous avons fixé la position du premier physicien, nous avons 6 façons de les positionner (3!). Ensuite, il nous reste 9 scientifiques à positionner, sans aucune contrainte, ce qui représente 9! façons de les positionner. En appliquant le principe multiplicatif, nous obtenons un total de 10 x 6 x 9! possibilités, soit environ 21 millions.
Pour la méthode des biologistes, nous devons rassembler les femmes et les hommes. Il y a donc deux façons de positionner ces deux groupes. Une fois que nous avons fait ce choix, nous devons permuter les positions à l'intérieur de chaque groupe. Pour les femmes, cela représente 6! façons de les positionner, et pour les hommes, cela représente également 6! façons. En appliquant le principe multiplicatif, nous obtenons un total de 2 x 6! x 6! possibilités, soit environ 1 million 36 800.
C'est ainsi que nous appliquons le comptage des permutations dans des petits exemples. Si vous avez d'autres questions, n'hésitez pas à consulter la FAQ.
Maths Spé
Probabilités
Terminale

Dénombrer des combinaisons
Dans ce cours, nous étudions les combinaisons en mathématiques. Une combinaison est le nombre de sous-ensembles que l'on peut obtenir à partir d'un ensemble plus grand. L'ordre n'a pas d'importance dans les combinaisons. Par exemple, au tirage du loto, l'ordre des numéros n'a pas d'importance car ce sont des cases que l'on coche.
Un autre exemple est le jeu de bridge où chaque joueur reçoit une main de 13 cartes. Le nombre de mains possibles est calculé en utilisant les combinaisons. Dans cet exemple, il s'agit d'un ensemble car une fois que l'on a les 13 cartes, l'ordre n'a plus d'importance. De plus, il n'y a pas de répétitions car on ne peut pas avoir deux fois la même carte.
Pour calculer le nombre de mains possibles, on peut utiliser la formule "13 parmi 52". Cela signifie choisir 13 éléments parmi un ensemble de 52 éléments. Il existe plusieurs méthodes pour effectuer ce calcul, soit en utilisant une calculatrice, soit en appliquant la formule de combinaison.
Ensuite, nous pouvons analyser les mains qui contiennent uniquement un cœur. Pour cela, on choisit d'abord un cœur parmi les 13 possibilités, puis on choisit les 12 cartes restantes parmi les 39 qui ne sont pas des cœurs. On multiplie ensuite les deux résultats car il n'y a pas de notion d'ordre et on obtient le nombre de mains possibles avec un cœur.
En résumé, il est important de savoir quand utiliser les combinaisons, c'est-à-dire lorsque l'ordre n'a pas d'importance et qu'il n'y a pas de répétition. Les combinaisons sont utiles pour calculer le nombre de sous-ensembles à partir d'un ensemble plus grand.
Maths Spé
Probabilités
Terminale

Combinaison et intersection
Dans ce cours, nous abordons l'utilisation des combinaisons avec les intersections. Nous prenons l'exemple de 20 élèves, parmi lesquels 14 aiment les maths, 7 aiment la physique et 4 aiment à la fois les maths et la physique. Pour mieux comprendre, nous utilisons un diagramme où 10 élèves aiment les maths, 4 aiment à la fois les maths et la physique, et 3 n'aiment que la physique. En déduisant cela, nous constatons qu'il y a 3 élèves qui n'aiment ni les maths ni la physique.
Ensuite, nous nous intéressons aux sous-groupes d'élèves et nous cherchons combien de sous-groupes de 4 élèves peuvent être formés parmi les 14 élèves qui aiment les maths. Comme il n'y a pas d'ordre et pas de répétition, il s'agit de combinaisons. La formule à utiliser est donc "14 parmi 4", ce qui donne 14! / (4! * 10!). Si nous simplifions cette expression en supprimant les termes communs, nous obtenons 14 * 13 * 12 * 11 / (4 * 3 * 2). Ce qui équivaut à 1001.
Ensuite, nous nous demandons combien de sous-groupes de 4 élèves ont exactement 2 élèves qui n'aiment que les maths et 2 élèves qui n'aiment que la physique. Pour cela, nous divisons le sous-groupe en deux parties, l'une avec les élèves qui n'aiment que les maths (10 élèves) et l'autre avec ceux qui n'aiment que la physique (3 élèves). Nous cherchons donc "2 parmi 10" et "2 parmi 3". En simplifiant ces expressions, nous obtenons 2 * 9 / 2 et 3. Le total est donc de 135 possibilités.
Ainsi, nous avons vu comment combiner les notions de combinaisons et d'intersections pour résoudre des problèmes décombinatoires.
Maths Spé
Probabilités
Terminale

Classique : jetons colorés
La méthode de dénouement utilisée dans ce cours consiste à faire un bilan des différentes variantes des jetons de couleurs utilisés. Les couleurs des jetons sont indiscernables, mais il y a des jetons blancs avec le numéro 0 et des jetons rouges avec le numéro 7.
Pour commencer, on tire simultanément 4 jetons, ce qui signifie qu'il n'y a pas d'ordre dans le tirage. On calcule ensuite le nombre de tirages possibles, en utilisant la formule des combinaisons. Dans ce cas, il y a 20 jetons au total et on en tire 4, donc il y a 4845 tirages possibles.
Ensuite, on s'intéresse aux tirages avec les quatre jetons ayant le même numéro. Il faut donc identifier les numéros qui sont présents au moins quatre fois parmi les jetons. Dans ce cas, les seuls numéros qui satisfont cette condition sont 0, 2 et 7. On compte alors le nombre de choix possibles pour chaque numéro et on additionne les résultats. Cela donne 67 tirages possibles.
La troisième question concerne les tirages avec uniquement des jetons blancs. On compte le nombre de jetons blancs disponibles (12) et on utilise la formule des combinaisons pour calculer le nombre de tirages possibles avec 4 jetons parmi ces 12. Il y a donc 495 tirages possibles.
Pour le quatrième cas, on cherche le nombre de tirages avec des jetons de la même couleur. On identifie les couleurs qui sont représentées avec plus de 4 jetons, ce qui donne les couleurs blanc et rouge. On compte le nombre de choix possibles pour chaque couleur et on additionne les résultats. Cela donne 565 tirages possibles.
Ensuite, il est demandé de former le nombre 2020 avec les jetons tirés. Comme l'ordre n'a pas d'importance dans un tirage simultané, on peut le considérer comme 2200 ou 0022. Il faut donc trouver le nombre de tirages possibles avec 2 jetons avec le numéro 2 parmi les 8 jetons disponibles et 2 jetons avec le numéro 0 parmi les 4 jetons disponibles. Cela donne 268 tirages possibles.
Enfin, on demande combien de tirages comportent au moins un jeton avec un numéro différent des autres. Plutôt que de chercher cet événement directement, il est plus simple de considérer l'événement contraire, c'est-à-dire des tirages avec tous les jetons identiques. On a déjà calculé le nombre de tirages de ce type, qui est de 76. On soustrait donc ce nombre du nombre total de tirages possibles pour obtenir le résultat final de 4739 tirages possibles.
Maths Spé
Probabilités
Terminale

Utiliser un arbre pondéré
Dans ce cours sur les probabilités, on utilise un arbre pondéré pour calculer les probabilités d'événements. On prend l'exemple de Naomi se rendant au lycée en vélo ou en bus, en fonction du temps qu'il fait. On sait que si le temps est ensoleillé, elle prend le vélo 8 fois sur 10, et si le temps est moche, elle prend le vélo 5 fois sur 10. On sait également que dans sa ville, 75% des journées sont insolubles. On cherche à déterminer la probabilité qu'elle prenne le vélo sachant qu'il fait beau, ainsi que la probabilité qu'elle prenne le vélo en général. Pour cela, on utilise la formule des probabilités totales et on trouve que la probabilité qu'elle prenne le vélo est de 72,5%.
Maths Spé
Probabilités
Terminale

Binomiale et tirage avec remise
Ce cours explique comment reconnaître et utiliser la loi binomiale. Il commence par définir le schéma de Bernoulli comme une expérience indépendante avec deux résultats possibles (échec ou réussite). Ensuite, il attribue une variable aléatoire x qui suit une loi binomiale de paramètres n et p, où n est le nombre de répétitions et p la probabilité de succès. La probabilité que x soit égal à k est calculée en utilisant la formule 1k parmi n fois p puissance k, 1 moins p puissance n moins k. L'exemple donné est celui de tirer des boules noires sur 8 boules, avec un succès de 3 boules noires sur 5 tirages. En utilisant la formule, la probabilité de réussite est trouvée à 20%. La conclusion est que savoir utiliser la loi binomiale est important pour résoudre des problèmes de probabilité.
Maths Spé
Probabilités
Terminale
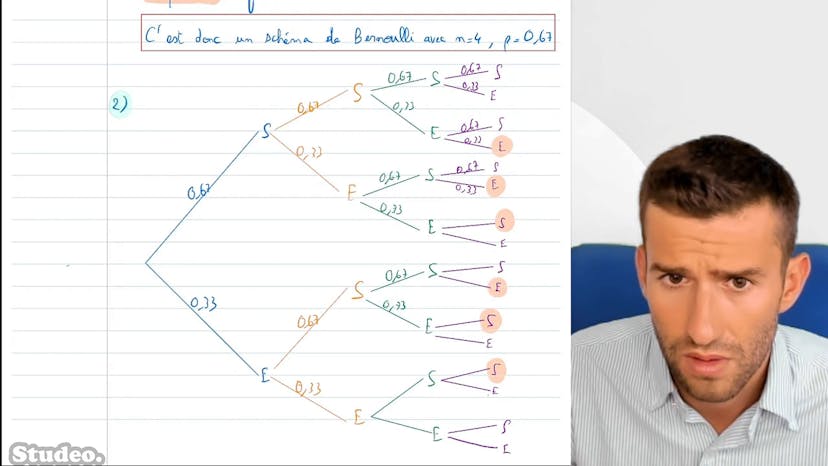
Représenter un schéma de Bernoulli
Ce cours présente une expérience de vente de livres en librairie où 67% des clients achètent un livre. Grâce à cette expérience répétée 4 fois et avec des clients indépendants, on peut appliquer le schéma de BR8. En utilisant un arbre pour représenter les différentes issues possibles, on peut calculer la probabilité d'avoir exactement 2 acheteurs de livres. Cette méthode est un peu laborieuse, mais peut être simplifiée en utilisant la formule de la loi binomiale.
Maths Spé
Probabilités
Terminale

Classique : produit défectueux en usine
Le cours traite des produits défectueux en usine et des tests indépendants pour déterminer s'ils sont vendables ou non. La probabilité qu'un produit défectueux soit mis en vente est calculée en utilisant les notations V, T1 et T2. La probabilité de vente est P de T1 inter T2, P de T1 fois P de T2 étant donné que les tests sont indépendants. La probabilité qu'au moins trois produits défectueux soient mis en vente dans une répétition de 100 expériences est calculée en utilisant la loi binomiale. La réussite est définie comme la vente, suivant les notations utilisées dans ce cours. Les calculs donnent une probabilité de 38% de chance de ne pas avoir de produits défectueux en vente, 36% de chance d'avoir un seul produit défectueux et 18% de chance d'avoir deux produits défectueux en vente. La probabilité qu'il y ait plus de trois produits défectueux en vente est de 7%. La formule classique de K par millienne, P à la puissance K, et 1 moins P à la puissance N moins K est utilisée pour les calculs.
Maths Spé
Probabilités
Terminale

Seuil de probabilité
Ce sous-chapitre traite des intervalles de fluctuation en relation avec les variables aléatoires et la loi binomiale. Il est essentiel de modéliser des événements et des probabilités dans la vie réelle, et cette modélisation peut être vérifiée avec des intervalles de fluctuation. Grâce à ces tests, on peut déterminer si une modélisation est effectivement précise ou non. À titre d'exemple, en supposant que x est le nombre de spectateurs, s'il y a moins de 10 personnes, une pièce de théâtre ne sera pas jouée. En utilisant la méthode des intervalles de fluctuation et des informations pertinentes sur les paramètres de la loi de probabilité et le seuil, on peut déterminer si la troupe est susceptible de jouer avec un intervalle de confiance de plus de 95%. En fin de compte, les intervalles de fluctuation peuvent être utilisés pour évaluer les modèles probabilistes dans la vie réelle.
Maths Spé
Probabilités
Terminale

Déterminer un intervalle de fluctuation
Nous cherchons à déterminer un intervalle de fluctuation centré pour une variable aléatoire X, avec n = 40, p = 0,2 et α = 0,05. Pour cela, nous calculons α/2, soit 0,025. Nous cherchons ensuite deux bornes k et i, telles que P(X<k) > 0,025 et P(X<i) > 0,025. Nous sommes ainsi en mesure de déterminer que k = 3 et i = 13. L'intervalle de fluctuation centré associé à X au seuil 0,095 est donc de 3 à 13, ce qui signifie que nous avons 95% de chances que X se situe dans cette plage.
Maths Spé
Probabilités
Terminale

Classique : efficacité d'un médicament ?
L'exercice consiste à calculer l'intervalle de fluctuation centré au seuil de 95% pour un médicament qui est efficace à 90% en prenant 400 patients malades. La loi G suit une loi binomiale de paramètres n égale 400 et p égale 0,9. On utilise la méthode de tâtonnement pour trouver la plus petite valeur de G telle que p de G inférieure à K, soit plus petite que 0,025 et la plus petite valeur de K telle que p de G inférieure à K soit inférieure à 0,975. On trouve que 95% de chance que le nombre de patients guéris soit situé entre 87% et 92,5%. L'hypothèse est donc validée et la borne inférieure de l'intervalle est de 87%. C'est un exercice typique de calcul d'intervalle de fluctuation pour l'efficacité d'un médicament.
Maths Spé
Analyse
Terminale
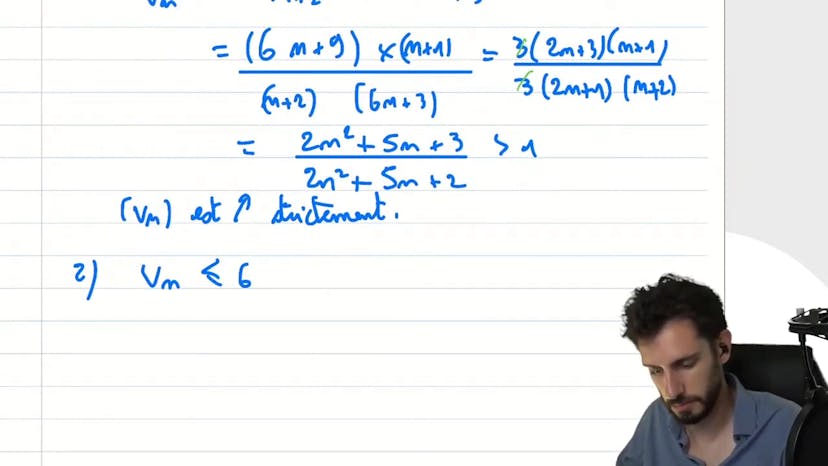
Suite-fraction
La vidéo parle de la convergence d'une suite donnée par vn = 6n+3 / (n+1). Pour étudier les variations, le professeur utilise le critère de croissance en comparant vn+1 / vn à 1. Après des calculs, il montre que ce ratio est strictement supérieur à 1, ce qui implique que la suite vn est strictement croissante. Ensuite, il montre que la suite est majorée par 6 en montrant que vn+3 égale à 6 pour tout n. Enfin, il applique le théorème de convergence monotone pour conclure que la suite vn converge. Le professeur propose également une méthode alternative où il simplifie l'expression de vn en écrivant vn = 6(n+1) - 3 / (n+1), permettant ainsi d'étudier les variations plus facilement. Il conclut en disant que la limite de la suite vn est égale à 6.


