Cours d'apprentissage en ligne

Conjecture puis récurrence

Dans ce cours, nous allons voir comment utiliser la démonstration par récurrence pour calculer la somme des entiers de 1 à n. La formule de la somme des entiers naturels est n(n + 1)/2. Pour utiliser la démonstration par récurrence, il faut connaître le résultat que l'on veut démontrer. Dans cet exemple, nous avons besoin de connaître la formule de la somme des entiers naturels. Nous commençons par poser la proposition p2n, qui est que la somme de 1 à n vaut n(n + 1)/2. Nous montrons ensuite que p2n est vrai pour tout n. Nous commençons par l'initialisation en vérifiant que la formule est vraie pour n = 1. Ensuite, nous passons à l'hérédité en supposant que p2n est vrai pour un n quelconque et nous voulons montrer que p2n+1 est vrai. Pour cela, nous remplaçons chaque occurrence de n par n + 1 dans l'expression au rang n. Nous appliquons la formule de la somme des entiers naturels à p2n et nous obtenons n(n + 1)/2 + n + 1. En simplifiant cette expression, nous obtenons n(n + 1)/2 + 2(n + 1)/2, ce qui donne (n + 1)(n + 2)/2. Ainsi, nous avons démontré que p2n+1 est vrai. En conclusion, d'après le principe de récurrence, nous avons prouvé que la somme des entiers de 1 à n est égale à n(n + 1)/2 pour tout entier naturel non nul n. C'est ainsi que nous pouvons utiliser la démonstration par récurrence pour calculer cette somme.

Hérédité : comment démarrer ?

La démonstration par récurrence est une méthode utilisée en mathématiques pour prouver une propriété pour tous les entiers naturels (n). Dans cette vidéo, l'accent est mis sur la démonstration de l'hérédité, qui est la partie la plus complexe de la méthode. Il existe deux cas possibles pour démontrer l'hérédité. Dans les deux cas, l'hypothèse de récurrence et ce que l'on veut montrer doivent être reliés. Le premier cas consiste à partir de l'hypothèse de récurrence (Pn) et à aboutir à Pn + 1. Le deuxième cas consiste à partir de Pn + 1 et à utiliser P2n pour conclure. Les deux méthodes sont possibles et peuvent être utilisées en fonction de l'exercice. Pour illustrer ces deux cas, un exemple simple est utilisé. Une suite (U) est définie par récurrence avec U0 = 5 et Un+1 = 3Un + 6. L'objectif est de montrer que U1 est strictement positif pour tout n. La démonstration commence par poser P2n, qui est U strictement supérieur à 0. L'initialisation ne pose aucun problème car U0 vaut 5. Ensuite, l'hérédité est démontrée en utilisant les deux cas possibles. Dans le premier cas, on part de l'hypothèse de récurrence (Pn) en supposant que U est supérieur à 0. En multipliant par 3 et en ajoutant 6, on obtient que 3Un + 6 est supérieur à 6, qui est lui-même supérieur à 0. Ainsi, Un+1 est supérieur à 0. Dans le deuxième cas, on part de Pn+1, c'est-à-dire de Un+1, et on utilise l'hypothèse de récurrence (Pn). Comme Un est supérieur à 0, on peut conclure que Un+1 est également supérieur à 0. Les deux méthodes sont possibles et peuvent être utilisées selon les besoins. Il n'y a pas de meilleure méthode, tout dépend de l'exercice. Si vous rencontrez des difficultés avec l'une des méthodes, vous pouvez essayer l'autre. En conclusion, la démonstration par récurrence est une méthode utilisée pour prouver une propriété pour tous les entiers naturels. L'hérédité, qui est la partie la plus complexe, peut être démontrée en utilisant deux cas possibles. Les deux méthodes sont viables et peuvent être utilisées en fonction des besoins de l'exercice.

Test video

Aucun résumé n'est disponible pour cette vidéo

Hérédité mais...

L'exercice consiste à démontrer que la proposition "9 divise 10 puissance n plus 1" est vraie pour tout entier naturel n. La question 1 demande de démontrer que si la proposition est vraie pour un entier n, alors elle est aussi vraie pour n plus 1. Pour cela, il faut utiliser le principe de récurrence. Le professeur souligne qu'il ne faut pas surinterpréter les énoncés et se focaliser uniquement sur la démonstration de l'imp

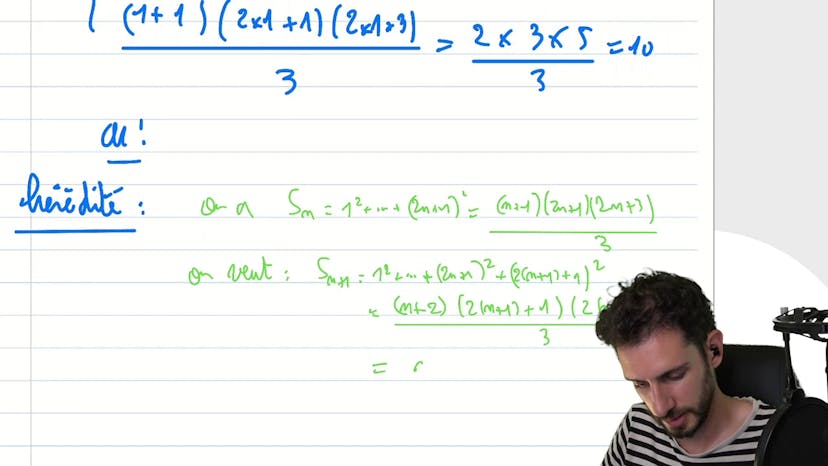
Avec une Somme

Ce cours traite d'une démonstration mathématique. L'objectif est de montrer que pour tout entier n, la somme des carrés des nombres impairs jusqu'à n est égale à la formule 2n + 3. Le cours commence par expliquer l'importance d'écrire clairement ce que l'on veut démontrer. Ensuite, l'auteur utilise des notations mathématiques pour étayer sa démonstration par récurrence. Il commence par l'initialisation, en montrant que l'égalité est vérifiée pour n = 1. Ensuite, il passe à l'hérédité, en supposant que l'égalité est vraie pour n, puis en démontrant qu'elle est également vraie pour n+1. Pour cela, il factorise certaines expressions et effectue des calculs, en utilisant la formule de la somme des impairs. En fin de compte, il conclut en montrant que l'égalité est vérifiée pour tout entier n.

Majoration 'simple'

Dans ce cours, nous cherchons à démontrer une propriété mathématique par récurrence. Nous commençons par initialiser la démonstration en montrant que pour n=1, la propriété est vérifiée. Ensuite, nous supposons que la propriété est vraie pour un certain n. Nous utilisons cette supposition pour montrer que la propriété est également vraie pour n+1. Pour cela, nous manipulons des équations et des inégalités afin de prouver que la propriété est conservée à chaque étape. Enfin, nous concluons que la propriété est démontrée pour tous les n.

Trop de puissance !

Le cours aborde le principe de trouver une suite définie par une relation de récurrence. Il explique que le processus pour trouver cette suite se fait en deux étapes : l'intuition du résultat et la démonstration de l'intuition par récurrence. L'exemple donné est une suite définie par u0 dans R, calculée en fonction de u0 et n, avec la relation un+1 = un^2. Le cours détaille l'intuition du résultat en calculant les premiers termes de la suite et en observant une pattern exponentielle. Ensuite, la démonstration par récurrence est effectuée pour prouver que la formule u0^2^n est valide pour tous les termes de la suite. L'importance de la démarche mathématique et de la capacité à se dépatouiller dans des exercices ambigus est soulignée. Cette compétence est considérée comme cruciale non seulement pour les études supérieures en mathématiques, mais également pour le baccalauréat.

Majoration plus costaude

Il s'agit d'un cours de mathématiques qui traite de la récurrence. L'objectif est de démontrer une relation mathématique en utilisant l'initialisation et l'hérédité. Dans cet extrait, l'enseignant explique comment utiliser la formule du sinus pour résoudre l'exercice. Il mentionne également l'utilisation de l'inégalité triangulaire pour simplifier les calculs. Il encourage les étudiants à connaître et à comprendre les différentes formules mathématiques afin de les utiliser efficacement dans leurs démonstrations. Le cours se termine par une conclusion sur l'importance de poser les bonnes questions pour résoudre les problèmes mathématiques.

test

Aucun résumé n'est disponible pour cette vidéo

Intro Suites et limites

Bienvenue dans cette vidéo d'introduction sur les limites de suite. Une limite de suite correspond à un point où les valeurs de la suite se rapprochent et semblent atteindre une valeur fixe, appelée plateau. Dans l'exemple donné, on voit une suite qui monte jusqu'à une certaine valeur, puis semble se coller à un plateau autour de la valeur 1. Plus la valeur de n augmente, plus la suite semble être proche de cette limite. Cependant, il faudra utiliser des définitions plus formelles pour être précis en mathématiques. Ces définitions peuvent sembler compliquées, mais il est important de les maîtriser. Un parallèle est fait avec l'étude de la dérivée, où au début on utilisait une définition et des calculs complexes, mais plus tard on a utilisé des tables de dérivées pour simplifier les choses. Pour les limites de suite, il y aura également des définitions formelles, mais aussi des tableaux de limites classiques à connaître. Le cours abordera la définition des limites en l'infini, en moins l'infini et en un point réel, ainsi qu'une propriété d'unicité des limites. Il y aura aussi une partie sur les limites de référence et les opérations possibles avec les limites, avec des tableaux à mémoriser. Enfin, il y aura une partie bonus sur les limites des suites géométriques. En termes de méthode, il y aura quatre approches principales : l'application de la définition formelle, la prédiction des limites grâce aux limites de référence et aux opérations, l'utilisation de techniques supplémentaires dans certains cas plus complexes, et enfin, un rappel sur la somme des termes d'une suite géométrique et les cas où cette somme peut avoir une limite. N'hésitez pas à poser des questions dans la FAQ et je vous retrouve dans la prochaine vidéo.

Limite finie

La limite réelle est la valeur vers laquelle une suite converge intuitivement lorsque n augmente. En mathématiques, on utilise la notion de couloir pour décrire plus précisément cette idée. Dans cette vidéo, je vais expliquer ce qu'est un couloir autour de la limite et montrer différentes façons de converger vers un réel, que ce soit de manière croissante, décroissante ou chaotique. La définition officielle de la limite dit que la suite Un converge vers un réel L si tout intervalle autour de L finit par contenir tous les termes de la suite à un certain moment. Pour vérifier cela graphiquement, je prends un couloir autour de la limite supposée. Si tous les termes de la suite sont inclus dans ce couloir à partir d'un certain moment, alors la limite est validée. Réduire la taille du couloir montre que les termes de la suite peuvent être de plus en plus proches de la limite, quelle que soit la distance choisie. En d'autres termes, on peut toujours se rapprocher autant que l'on souhaite de la limite. Je présente ensuite quelques exemples de suites qui convergent vers 2, que ce soit de manière croissante, décroissante ou en oscillant. Ces différents cas montrent qu'il existe plusieurs façons de converger vers une limite. J'invite les spectateurs à poser leurs questions ou demander des précisions dans la FAQ et je termine en annonçant la prochaine vidéo. En résumé, cette première vidéo sur la définition des limites explique la notion de couloir autour d'une limite réelle et montre différentes façons de converger vers cette limite.