 Tous les sujets
Tous les sujets Maths
Maths Physique-Chimie
Physique-Chimie Corrigés de BAC
Corrigés de BAC Révisions Maths lycée
Révisions Maths lycée Prépa Examens
Prépa Examens
Terminale
Première
Seconde
MPSI/PCSI
2BAC SM Maroc
 Tous les sujets
Tous les sujets Maths
Maths Physique-Chimie
Physique-Chimie Corrigés de BAC
Corrigés de BAC Révisions Maths lycée
Révisions Maths lycée Prépa Examens
Prépa Examens
Maths Spé
Analyse
Terminale

TVI et calculs costauds !
La fonction f(x) = 2/(e^x + e^(-x)), où x appartient à R, est étudiée dans ce cours. Après une analyse graphique, il est montré que cette fonction admet une seule solution sur R à l'équation f(x) = x.
Ensuite, la fonction g(x) = f(x) - x est introduite. Les limites de g(x) lorsque x tend vers plus l'infini et moins l'infini sont calculées, confirmant que g(x) tend vers 0 dans les deux cas.
La deuxième partie du cours consiste à montrer que g(x) est décroissante. D'abord, l'idée de représenter g(x) comme une somme de fonctions décroissantes est évoquée, mais est rejetée car f(x) n'est pas décroissante. Par conséquent, le calcul des dérivées est utilisé pour déterminer que g(x) est décroissante.
En fin de compte, il est prouvé que g(x) est strictement décroissante, et un tableau de variations de g(x) est dressé pour montrer qu'il n'y a qu'une seule solution à l'équation f(x) = x, ce qui confirme les résultats obtenus précédemment.
Maths Spé
Analyse
Terminale

Exp : indéterminée en -∞
Dans cet exercice, on nous donne une fonction F2X et on nous demande de déterminer sa limite en plus l'infini, sa courbe CF comme asymptote horizontale et ses variations de f'E2X. Tout d'abord, on applique notre maîtrise des puissances pour simplifier la fonction F2X. Ensuite, on remplace petit x par moins grand x sur E de grand x, et on utilise des formules simples pour trouver la limite de la fonction. On en déduit que la courbe CF a une asymptote horizontale. Pour la variation de f'E2X, on calcule la formule du produit et on en déduit un petit tableau de variations. Finalement, on retrouve les limites que nous avions trouvées précédemment. La limite de f'F en plus l'infini est un plus 1, donc elle admet une asymptote horizontale y égale 1.
Maths Spé
Analyse
Terminale

Vers la SUP : Quantité conjuguée
Dans cet exercice, il y a une somme finie de n termes avec x qui tend vers l'infini. Il est important de remarquer que c'est x qui tend vers l'infini et non pas n. Il y a des racines avec un signe moins, il s'agit de la méthode de quantité conjuguée à appliquer. Il y a n termes dans la somme qui sont compensés par n termes ailleurs. En utilisant cette méthode, il est possible de réécrire la somme en utilisant chaque racine avec un petit compagnon. En multipliant chaque terme par quantité conjuguée, on obtient une identité remarquable qui tend vers 0 lorsque x tend vers plus l'infini. La réponse est donc que la somme tend vers 0. Pour résoudre cet exercice, il est important de dépasser ses peurs et ses stress, analyser calmement la situation en se rappelant des méthodes et des astuces du cours.
Maths Spé
Analyse
Terminale

Étude f : Niveau MPSI mais outils de première !
Ce cours traite de l'étude d'une famille de fonctions de la forme E(2x)/x^n, où n est un entier naturel non nul. On commence par déterminer l'ensemble de définition de ces fonctions, en excluant les valeurs de x pour lesquelles le dénominateur est nul. Ensuite, on examine la dérivabilité de ces fonctions, qui dépend uniquement de la dérivabilité de l'exponentielle et des polynômes. Ensuite, on suppose que n est pair et on dresse le tableau de variations de la fonction f, en analysant notamment les signes des expressions E(2x) et x^(n-1) pour déterminer les variations de f'. On déduit ensuite les limites de la fonction f pour x tendant vers l'infini et vers zéro. Enfin, on étudie le cas où n est impair et on effectue les mêmes étapes pour déterminer les variations et les limites de f dans ce cas.
Maths Spé
Analyse
Terminale

Dérivabilité avec valeur absolue ?
Dans cet exercice, nous devons démontrer que la fonction donnée est continue et dérivable sur R, à l'exception de x=0.
Tout d'abord, nous vérifions que la fonction 1+x est définie sur R, car pour tout x, 1+x est strictement supérieur à 0. Ainsi, il n'y a pas de problème de définition.
Ensuite, nous observons que le quotient de deux fonctions continues donne une fonction continue, ce qui confirme que notre fonction est continue sur R.
En ce qui concerne la dérivabilité, nous constatons que pour tout x différent de 0, la fonction est dérivable puisque x et 1+x sont dérivables sur R, à l'exception de x=0.
Nous supposons donc que la fonction sera également dérivable en x=0. Cette supposition est basée sur le fait que la fonction semble être assez lisse et ne présente pas de rupture de pente.
Nous déterminons ensuite l'expression de la fonction en fonction du signe de x. Au point 0, nous constatons que les limites à gauche et à droite de la fonction sont identiques, confirmant ainsi sa continuité.
Pour démontrer que la fonction est dérivable sur R à l'exception de x=0, nous calculons les dérivées des nombres dérivables en 0. En utilisant des astuces mathématiques, nous obtenons les expressions des dérivées à gauche et à droite de x=0.
En calculant les dérivées en x=0, nous obtenons des valeurs différentes pour chaque côté, confirmant ainsi que la fonction n'est pas dérivable en x=0.
En conclusion, la fonction donnée est continue sur R et dérivable sur R à l'exception de x=0.
Maths Spé
Analyse
Terminale
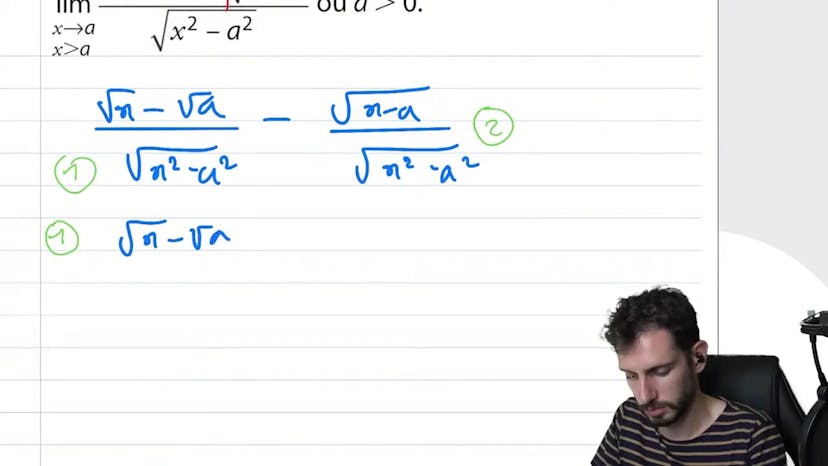
Quantité conjugée piégeuse
Le cours traite des quantités conjuguées et comment les utiliser correctement pour éviter les erreurs. L'auteur donne un exemple et explique pourquoi une certaine approche ne fonctionne pas. Il propose une solution en séparant la fraction en deux parties et en utilisant une quantité conjuguée pour simplifier l'expression. Ensuite, l'auteur gère chaque partie séparément et fait les calculs nécessaires pour arriver à la fonction finale. La fonction finale est donnée sous une forme simple et optimisée pour le SEO.
Maths
Analyse
Première

La forme canonique
La première méthode classique pour résoudre ce problème est d'utiliser la mise en forme canonique. Cette méthode consiste à passer d'une forme développée à une forme canonique où il n'y a qu'un seul terme contenant du x.
Pour ce faire, on repère d'abord les facteurs communs. Dans cet exemple, on peut factoriser par 4 et même par -4 pour simplifier les étapes suivantes. On obtient ainsi moins 4x², moins 2x et plus 3.
Ensuite, on repère le début du développement d'un carré avec les deux termes contenant du x. Dans cet exemple, le terme x²-2x est quasiment équivalent à x²-2x plus 1, auquel on soustrait 1. Donc on doit ajouter et soustraire 1 pour maintenir l'équivalence.
On obtient ainsi la forme x²-2x plus 1, que l'on peut simplifier en (x-1)² moins 1.
Pour réécrire la fonction f2x égale moins 4 fois x-1² moins 1, plus 3, on peut simplifier en moins 4 facteur de (x-1)² plus 2.
Pour résoudre l'équation f2x égale moins 8 en utilisant la forme canonique, on développe la formule f2x et on obtient moins 4 fois (x-1)² moins 4 fois 2 est égal à moins 8.
En simplifiant, on obtient que moins 4 fois (x-1)² est égal à 0. Le facteur moins 4 peut être supprimé et on obtient que (x-1) doit être égal à 0, donc x égal à 1.
Maths
Analyse
Première

Tableau de variations
Ce cours traite du sens de variation d'une fonction polynôme, en fonction du signe de son coefficient principal 'a'. Lorsque 'a' est positif, la fonction avance en décroissant puis en croissant (fonction qui sourit), alors que lorsque 'a' est négatif, la fonction avance en croissant puis en décroissant (fonction qui fait la tête). En appliquant une formule pour trouver le minimum et le maximum de la fonction, liés aux valeurs de 'a', on peut facilement déterminer le sens de variation de n'importe quelle fonction polynôme. En appliquant cette méthode à des exemples concrets, l'auteur démontre que la formule n'est pas très compliquée une fois qu'on la comprend.
Maths
Analyse
Première

Racines
Dans ce cours, nous avons vu différentes méthodes pour trouver des racines de fonctions polynomiales. Pour le premier exemple, on peut calculer le delta ou utiliser la forme canonique de la fonction. Pour le deuxième exemple, on peut repérer une densité remarquable ou utiliser une racine évidente pour trouver les autres racines. Pour le troisième exemple, il est possible de factoriser la fonction et repérer des racines évidentes. En somme, il est utile de connaître certaines formules et de tester différentes valeurs pour trouver les racines.
Maths
Analyse
Première

La Forme Factorisée
Dans ce cours de mathématiques, nous avons vu plusieurs exemples de facteurisation de trinômes. Pour le premier, nous avons utilisé une astuce pour factoriser f2x = -0,5x² + 5x - 12,5 en utilisant -0,5 comme facteur commun. Pour le deuxième, nous avons cherché une racine évidente en remarquant que les coefficients semblaient s'approcher de zéro pour x = 1. Nous avons ainsi trouvé que g² = 4x² + 4x - 8 = (x-1)(x+2). Pour le troisième exemple, nous avons utilisé la méthode du delta pour trouver que h²x = 3x² - 2x + 2,4 n'était pas factorisable. Nous avons également montré qu'il était possible d'obtenir la forme canonique x² - (2/3)x + 1/9 en faisant un petit calcul. En somme, nous avons vu différentes méthodes pour factoriser des trinômes et comment les utiliser en fonction de la situation.
Maths
Analyse
Première

Astuce : les racines évidentes
Dans ce cours, on parle de la notion de racine évidente dans les fonctions ax² plus bx plus c. Si le discriminant est positif et qu'il existe deux racines, on a des relations entre les racines et les coefficients comme le produit des deux racines égal à c sur a et la somme des deux racines égale à moins b sur a. Tester des racines évidentes peut être utile dans les cas où les coefficients semblent pouvoir se combiner facilement pour faire 0. L'exercice consiste à trouver toutes les solutions de la fonction f²x égal à 5x² moins 4x moins 1. En trouvant que moins 1 est racine évidente, on peut trouver que l'autre racine est moins 1 cinquième. L'objectif de cet exercice est d'entraîner l'esprit à développer des réflexes pour détecter des choses rapidement afin d'aller plus vite dans des exercices plus complexes en première ou en terminale.
Maths
Analyse
Première
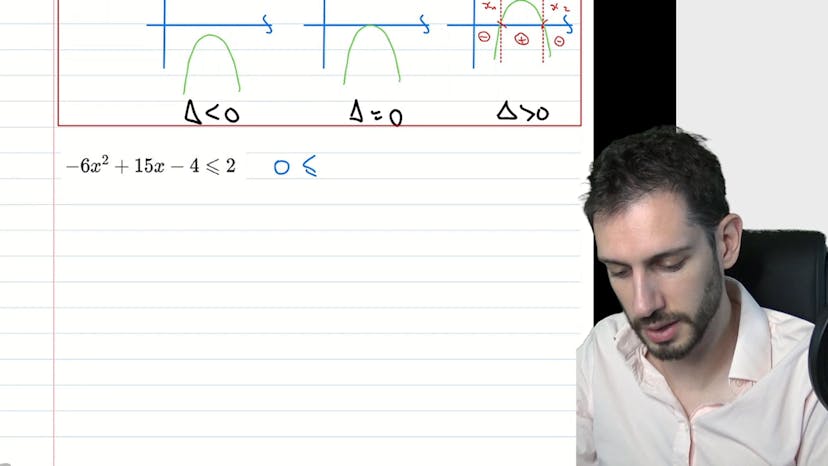
Les inéquations
Ce cours traite de la résolution d'inéquations avec des polynômes de degré 2. Pour comprendre le comportement des fonctions polynômes en fonction de A, B et C, on peut se référer à leur forme en sourire ou en tête, déterminée par la valeur de A. Lorsque delta est négatif, la fonction ne croise jamais l'axe des x et est toujours positive stricte. Si delta est égal à 0, la fonction est nulle en un seul point mais toujours positive. Enfin, si delta est positif, la fonction est un peu plus basse que les précédentes et croise deux fois l'axe des x. Il suffit ensuite de tout mettre du même côté d'une équation pour avoir quelque chose plus grand ou plus petit que 0. Ensuite, on peut factoriser et calculer delta pour trouver les racines de la fonction. Ensuite, on peut tracer un tableau de signes pour déterminer la solution de l'inéquation.


