Cours d'apprentissage en ligne

Physique

Van der Waals

Dans cette vidéo, on découvre que l'équation d'état des gaz parfaits, notre équation préférée dans ce chapitre, est en fait un cas particulier d'une équation plus générale, l'équation de Van der Waals. Cette équation relie la pression, le volume et la température d'un fluide à l'aide de deux constantes positives, A et B, qui caractérisent le fluide. Pour une mole de gaz, l'équation devient P + A/V^2(V-B) = RT. Il est possible de généraliser cette équation de Van der Waals pour N moles de fluide en prenant en compte le comportement des variables (pression, volume et température) lors du passage d'un système d'une mole à un système de N moles. La pression est une variable intensive, ce qui signifie qu'elle conserve sa valeur lorsqu'on combine deux sous-systèmes indépendants. La température est également une variable intensive. En revanche, le volume est une variable extensive, ce qui signifie qu'il augmente proportionnellement au nombre de moles de gaz. En remplaçant V par V' = nV, où n est le nombre de moles de gaz, dans l'équation de Van der Waals, on obtient une version de l'équation pour un système constitué de N moles. En multipliant l'équation initiale par n, on retrouve V' dans l'équation. En posant A = 0, on étudie l'influence de B, appelé covolume, qui représente l'effet de répulsion à courte distance entre les molécules. Pour l'hydrogène, on donne une estimation approximative de B en se basant sur la distance de liaison entre deux atomes d'hydrogène. En posant B = 0, on étudie l'influence de A, qui représente l'effet attractif à courte distance entre les atomes. A a un effet opposé à B, avec un signe positif. Le terme correctif de la pression dans l'équation de Van der Waals est une fonction décroissante du volume. Cela s'explique par le fait que plus le volume est important, moins l'effet attractif entre les atomes est intense. L'effet attractif perd en intensité lorsque les atomes sont éloignés les uns des autres, ce qui est pénalisé en divisant par V². En conclusion, cet exercice permet de manipuler et d'analyser l'équation de Van der Waals, en comprenant ses différentes constantes et leurs effets sur la pression, le volume et la température des fluides.

Physique

Double compartiment

Dans cette vidéo, Mathilis examine une enceinte à double compartiment contenant de la vapeur d'eau. L'enceinte a un volume de 10 litres et est dilaterme. Un piston de masse M et de surface S sépare les deux compartiments, avec 1,0 mol d'eau dans le compartiment supérieur et 0,10 mol d'air dans le compartiment inférieur. On considère que la vapeur d'eau et l'air sont des gaz parfaits. Pour déterminer la fraction molaire de vapeur d'eau, on doit trouver la quantité de matière de vapeur dans l'enceinte. Cela peut être trouvé en utilisant l'équation d'état des gaz parfaits, en utilisant la pression, le volume et la température. La pression est fixée à la pression de vapeur saturante à 100°C, qui est de 1 bar. Le volume est déterminé en utilisant le théorème fondamental de la statique et l'équation des gaz parfaits. En utilisant ces informations, on trouve que la fraction molaire de vapeur d'eau est de 27%. Il est également noté qu'une hypothèse a été faite au départ selon laquelle le volume du liquide est négligeable par rapport au volume du gaz, ce qui est justifié par le rapport de 1:2000 entre les volumes du gaz et du liquide. En conclusion, il est important de prendre son temps pour comprendre la problématique et de mettre en place une démarche appropriée pour résoudre ce type d'exercice en thermodynamique.

Physique

Libre parcourt moyen

Dans cette vidéo, nous abordons la notion de libre parcours moyen, qui concerne la réalité microscopique des molécules. Le libre parcours moyen désigne la distance moyenne qu'une molécule parcourt avant de rencontrer une autre molécule. Pour le dioxygène à pression atmosphérique et à température ambiante, le libre parcours moyen est d'environ 100 nanomètres. Pour comprendre le libre parcours moyen, nous considérons les molécules comme des sphères indéformables de diamètre d. Une molécule en mouvement entre en collision avec une autre molécule si le centre de la molécule en mouvement se situe à une distance inférieure à d de la trajectoire de la molécule fixe. On peut délimiter un cylindre de base πd² de hauteur L, où L représente le libre parcours moyen. Nous pouvons définir le libre parcours moyen, L, comme la distance moyenne parcourue par une molécule avant de rencontrer une autre molécule dans ce cylindre. La hauteur limite à laquelle une molécule peut être placée sans entrer en collision est d. Le libre parcours moyen, L, peut être exprimé en fonction du diamètre des molécules, d, et du nombre de particules par unité de volume, N. En utilisant le nombre d'Avogadro, Na, la constante de Boltzmann, KB, la pression atmosphérique P0 et la température T, nous pouvons obtenir une formule : L = 1/(Na * π * d² * N*). Pour évaluer la taille des molécules dans le modèle du gaz parfait, nous utilisons la formule précédente et l'équation d'état du gaz parfait (P0 = N * KB * T / V) pour exprimer N en fonction de P0, T et d'autres constantes. Enfin, nous évaluons la taille D des molécules dans le modèle du gaz parfait en utilisant les valeurs numériques correspondantes et obtenons D = 0,36 nanomètre. En commentant la valeur de D obtenue (0,36 nanomètre) par rapport à la taille d'une molécule de dioxygène (0,29 nanomètre), nous concluons que le modèle du gaz parfait et du libre parcours moyen peuvent décrire assez précisément les molécules de dioxygène. Cependant, il faudrait étudier d'autres molécules pour savoir si cette loi se généralise.

Configuration électronique

Salut à tous ! Aujourd'hui, nous allons travailler sur la classification périodique. L'exercice consiste à trouver la configuration électronique du brome et de son ion correspondant, en utilisant les configurations électroniques des gaz rares argon et krypton. Pour rappel, il y a quelques règles à suivre lorsqu'on parle de configuration électronique. La règle de Shlekovski indique que les atomes sont classés par énergie croissante et par ordre croissant du nombre quantique N + L. Ensuite, nous avons le principe de Pauli qui stipule que deux électrons ne peuvent pas être décrits par les mêmes nombres quantiques. Pour le brome (Br), nous commençons par remplir les couches dans l'ordre croissant. Nous avons la 1S, puis la 2S, la 3P, la 3S, la 3P, la 4S, la 3D, et enfin la 4P. La configuration se termine avec 4P5. En utilisant les configurations électroniques des gaz rares, nous pouvons écrire la configuration condensée du brome comme suit : [Kr] 5s² 4d¹⁰ 4p⁵. Ensuite, nous passons à l'ion du brome (Br-). Nous devons réorganiser la configuration électronique en ordre croissant de n pour savoir quel électron doit être retiré. Ainsi, nous plaçons la sous-couche 3D10 avant la 4S2 et la 4P5. L'ion Br- est donc représenté par la configuration électronique [Kr] 5s² 4d¹⁰ 4p⁶, ce qui est la même configuration que le krypton (Kr). En ce qui concerne les électrons de cœur et de valence de l'atome de Br- et du Br, les électrons de cœur sont ceux qui se trouvent dans les couches déjà remplies, tandis que les électrons de valence sont ceux dans les sous-couches en cours de remplissage. Pour l'ion Br-, les électrons de cœur comprennent la configuration de l'argon (3d¹⁰), tandis que les électrons de valence sont 4s² 4p⁶. J'espère que ce résumé vous a été utile. N'hésitez pas à poser vos questions en commentaire. À bientôt !

Atome d'hydrogène

Dans cette vidéo, Leïla explique la configuration électronique de l'atome d'hydrogène et la physique quantique liée à ses niveaux d'énergie. Elle donne la formule ΔE = hµ = hc/λ pour la désexcitation des électrons et mentionne que la longueur d'onde de la radiation entre les niveaux d'énergie E4 et E2 est demandée dans cet exercice. En utilisant la formule de Planck-Einstein, elle isole λ et obtient hc/(E4-E2). En appliquant les valeurs numériques, elle trouve λ = 482 nm, ce qui correspond à la plage du visible. Elle souligne également la confusion fréquente entre les couleurs du spectre visible et les termes ultraviolet et infrarouge, rappelant que le bleu se trouve vers 400 nm et le rouge vers 800 nm.

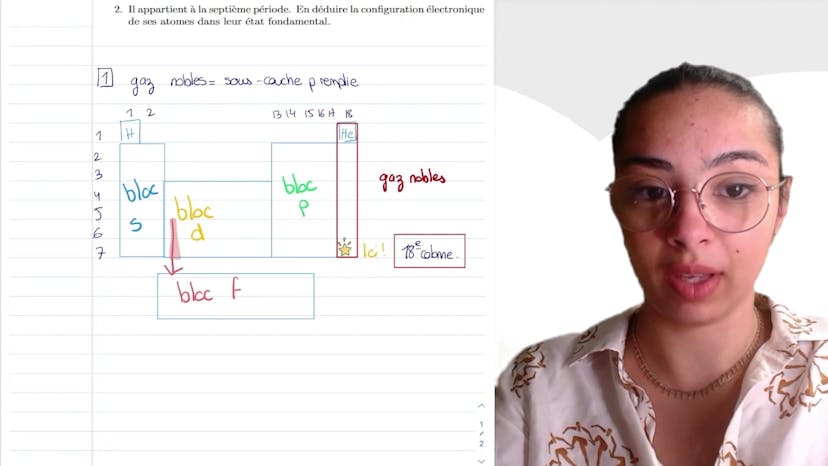
L'élément mystère

Dans ce cours, Leïla explique comment retrouver et définir la configuration électronique d'un élément mystère à partir de la classification périodique. Elle commence par expliquer la notion de gaz nobles, qui sont des éléments stables avec une configuration électronique en P6. Elle présente ensuite schématiquement le tableau de la classification périodique, qui est constitué des blocs S, B, D et F. Elle explique que l'hélium est placé dans la colonne des gaz nobles en raison de sa similarité avec eux, bien qu'il devrait en réalité être placé dans la deuxième colonne, première période. Ensuite, Leïla indique que l'élément en question doit être placé dans la colonne 18 et la 7e période de la classification périodique. Elle donne ensuite deux approches pour déterminer la configuration électronique de cet élément : utiliser le tableau précédent ou appliquer la règle de Tchlékovski. Elle préfère utiliser le tableau et montre que la structure électronique sera celle du radon : 5F14, 6D10, 7S2 et 7P6. Elle conclut en soulignant l'utilité de connaître ce sujet pour les examens de chimie.

Quelques familles d'éléments

Aujourd'hui, dans ce cours sur les familles d'éléments chimiques, nous allons examiner différentes familles et leurs propriétés en termes de classification. Commençons par le calcium, qui appartient à la famille des alcalins terrestres. On nous demande de trouver l'ion monoatomique stable qu'il peut former. Pour cela, il faut se rappeler des différentes colonnes auxquelles correspondent les familles. Les alcalins terrestres se trouvent dans la deuxième colonne. Ils ont des propriétés physiques importantes. En général, les éléments ont besoin d'avoir la structure électronique d'un gaz noble pour être stables. Le calcium se trouve dans la première colonne, tandis que les gaz rares se trouvent dans la dix-huitième colonne. Ainsi, le calcium souhaite avoir la même configuration électronique qu'un gaz rare qui se trouve juste avant lui. Par conséquent, il aimerait perdre deux électrons pour obtenir cette configuration. Il forme donc l'ion Ca2+. Ensuite, nous avons l'iode, qui est un halogène. Les halogènes se trouvent dans l'avant-dernière colonne. Ils forment des ions I-. Pour nommer l'iode, on utilise le suffixe "-iodure" (comme pour les autres halogènes tels que le brome). Lorsqu'il s'agit de déterminer le nombre de liaisons que les atomes peuvent former pour s'entourer d'autres électrons de valence, il faut se référer aux schémas de Lewis pour la configuration des molécules. Dans ce cas, nous nous concentrons sur les atomes individuels. Les atomes forment des liaisons covalentes lorsqu'ils partagent des électrons pour atteindre la structure électronique d'un gaz rare. L'hydrogène a un électron de valence et aimerait en avoir deux pour atteindre la structure de l'hélium. Il forme donc une seule liaison. Le carbone a quatre électrons de valence et souhaite en avoir huit. Il forme donc quatre liaisons pour atteindre cet objectif. L'azote a cinq électrons de valence et aimerait en avoir huit. Il forme donc trois liaisons. Enfin, le chlore a sept électrons de valence et aimerait en avoir huit. Il forme donc une liaison ou gagne un électron pour devenir un ion chlorure. J'espère que cette transcription vidéo vous a été utile. N'hésitez pas à poser vos questions en commentaire.

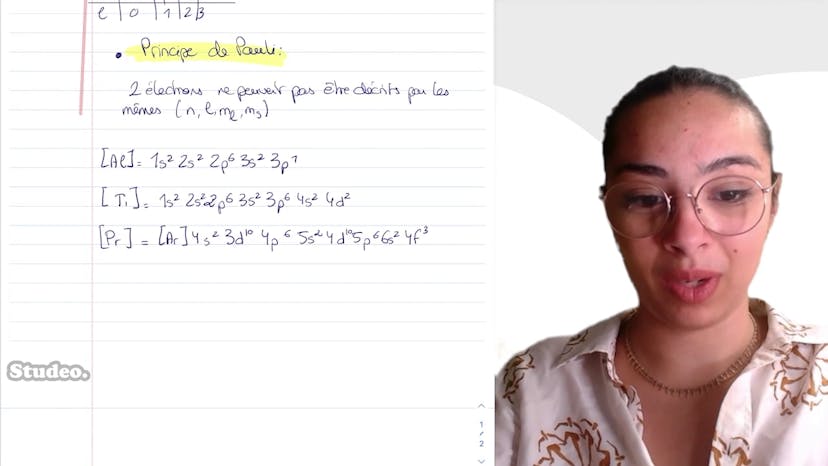
Encore des configurations électroniques

Dans cette vidéo, Leïla explique comment déterminer les configurations électroniques de l'aluminium, du titanium et du préséodyme dans leur état fondamental. Elle rappelle les règles pour déterminer les configurations électroniques: la règle de Schlickowski qui dit que les couches sont remplies selon l'ordre croissant de n plus l, et en cas d'égalité, selon n croissant, et le principe de Pauli qui dit que deux électrons ne peuvent pas être décrits par le même quadruplet de nombres quantiques. Elle donne les configurations électroniques suivantes: - Aluminium: 1s2 2s2 2p6 3s2 3p1 - Titanium: 1s2 2s2 2p6 3s2 3p6 4s2 4d2 - Préséodyme: 4s2 3d10 4p6 5s2 4d10 5p6 6s2 4f3 Elle explique ensuite la répartition des électrons dans les sous-couches non saturées, en utilisant la règle de Hund qui dit que les électrons occupent un maximum d'orbitales atomiques avant de s'apparier si les orbitales sont dégénérées. Les orbitales sont dégénérées si elles sont au même niveau d'énergie. Elle donne les répartitions suivantes: - Pour l'aluminium: 3p1 avec un seul électron - Pour le titanium: 4d2 avec un électron dans chaque orbitale - Pour le préséodyme: 4f3 avec un électron dans chaque orbitale, et une paire d'électrons appariés dans une orbitale Elle conclut en disant que ces connaissances sont utiles pour les devoirs surveillés et encourage les spectateurs à poser des questions dans les commentaires.

Le calcium

Aujourd'hui, nous allons parler du calcium, le troisième élément de la famille des alcalinotéreux. Le numéro atomique du calcium est 20 et sa configuration électronique est 1S2, 2S2, 2P6, 3S2, 3P6, 4S2. Les éléments de la famille des alcalinotéreux se terminent en S2 dans leur configuration électronique. Le calcium se trouve dans la deuxième colonne de la classification périodique. En ce qui concerne les ions, le calcium forme généralement un ion Ca2+ en perdant ses deux électrons de la couche externe 4s, ce qui lui confère la configuration électronique de l'argon. En ce qui concerne les valeurs des énergies de première ionisation, elles diminuent du béryllium au barium dans la famille des alcalinotéreux. Cela signifie que les électrons de la couche S sont de moins en moins liés au noyau. Lorsque le numéro atomique augmente, les électrons deviennent plus stables. J'espère que cette vidéo sur le calcium et les alcalinotéreux vous a été utile. N'hésitez pas à poser vos questions ou à faire des commentaires.

L'oxygène

L'oxygène et l'azote ont les configurations électroniques suivantes : 1s² 2s² 3p4 et 1s² 2s² 3p3 respectivement. Les énergies de première et de seconde ionisation sont spécifiques à chaque élément. La première ionisation consiste à arracher le premier électron d'un atome, tandis que la deuxième ionisation consiste à arracher le deuxième électron. Contrairement à ce que l'on pourrait penser, la deuxième ionisation ne se fait pas en une seule fois, mais par étapes. Les atomes de lithium, de bore et d'oxygène présentent des singularités dans leurs énergies d'ionisation. Par exemple, le lithium atteint une grande stabilité avec sa configuration électronique de Li+, ce qui rend l'arrachement du deuxième électron difficile et donc rend Li2+ moins stable. De manière similaire, le bore et l'oxygène ont des énergies d'ionisation spécifiques en raison de leurs configurations électroniques. Ces exemples illustrent que la stabilité des ions dépend de leurs configurations électroniques.

Autour de l'hydrogène

Dans cette vidéo, Leïla parle des séries de Balmer pour l'hydrogène et le deutérium, qui correspondent aux désexcitations vers le niveau d'énergie n = 2. Elle explique que la formule pour calculer ces longueurs d'onde est 1/λ = R(1/n^2 - 1/p^2), avec p > n. Elle montre ensuite comment calculer la constante de Rydberg avec 5 chiffres significatifs pour le deutérium en utilisant une régression linéaire. Leïla poursuit en abordant le nombre maximum d'électrons pouvant être contenus dans un niveau d'énergie N. Elle donne des exemples pour les niveaux N = 1, 2, 3 et 4, en montrant que la formule 2N^2 fonctionne pour ces cas. Ensuite, elle aborde la définition de l'affinité électronique de l'hydrogène, qui est l'énergie d'attachement nécessaire pour former l'ion H-. La réaction associée est H+ + e- → H-. Leïla souligne l'importance de connaître cette définition, même si elle est moins souvent demandée que l'énergie d'ionisation. Enfin, Leïla parle de la table donnant les affinités électroniques, indiquant que l'énergie d'attachement est faible mais positive, et la plus faible dans chaque période. Elle explique que les éléments ayant la plus faible énergie d'ionisation sont les alcalins, car ils ont tendance à vouloir être ionisés pour atteindre la structure électronique des gaz rares. C'est ainsi que se termine la vidéo, et Leïla encourage les spectateurs à poser des questions ou à faire des remarques dans les commentaires.