Cours d'apprentissage en ligne

Bac Maths

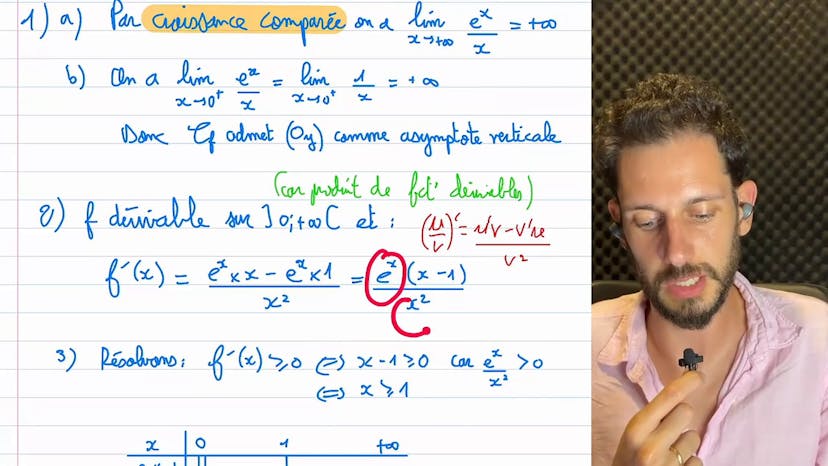
Fonctions exponentielle - Métropoles 2021

Aucun résumé n'est disponible pour cette vidéo

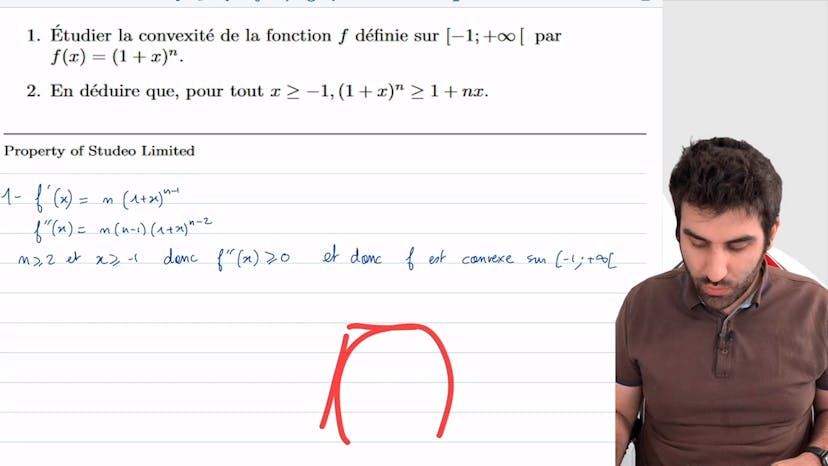
iné

Dans cet exercice, on démontre l'inégalité de Bernoulli en utilisant la convexité de la fonction 1 plus x puissance n. Pour commencer, on étudie la convexité de cette fonction en dérivant deux fois et en analysant les signes des dérivées. On conclut que la fonction est convexe sur l'intervalle moins 1 plus l'infini. Ensuite, on applique cette propriété pour montrer que pour tout x plus grand que moins 1, 1 plus x puissance n est supérieur à 1 plus nx. On utilise le fait qu'une fonction convexe est au-dessus de ses tangentes pour établir cette inégalité. Finalement, on déduit que sur l'intervalle moins 1 plus l'infini, 1 plus x puissance n est toujours supérieur à 1 plus nx.

Le lancer de gerbe de paille (1)

Aucun résumé n'est disponible pour cette vidéo

Le lancer de gerbe de paille (2)

Dans cette vidéo, nous abordons un aspect électrique lié au microphone utilisé par l'animateur lors d'une compétition de lancé de Gerbe de Paille. Le microphone est un transducteur électro-acoustique qui convertit les signaux acoustiques en signaux électriques. Le schéma du microphone est présenté avec un condensateur composé de deux armatures. Lorsque le microphone capte un son, la distance entre les deux armatures varie. Pour que le condensateur fonctionne, il doit être chargé à l'aide d'une source de tension continue de 48 volts. On utilise ensuite la loi des mailles pour établir la relation entre la tension de la source E, la tension aux bornes du condensateur UC et la tension aux bornes de la résistance UR. En appliquant cette loi, on obtient l'équation différentielle de la forme E = RC * d(UC)/dt + UC. On mesure la tension UC aux bornes du condensateur pendant la charge et on obtient une courbe qui peut être modélisée par trois fonctions mathématiques. En analysant les limites de ces fonctions, on conclut que la fonction qui correspond à la charge du condensateur est UC = E * (1 - exp(-t/RC)). On vérifie ensuite que cette fonction satisfait l'équation différentielle. On précise ensuite que la capacité d'un condensateur plan est donnée par C = E * S / d, avec E la permittivité de l'air entre les armatures du condensateur. On nous donne le produit de la permittivité de l'air par la surface S, qui est égal à 1,4 * 10^-15 farad mètre. En utilisant cette relation, on détermine la distance d entre les deux armatures du condensateur lorsque le microphone fonctionne mais ne capte pas de son, et on obtient d = 20 micromètres. Enfin, on explique que lorsque la membrane du microphone se déplace sous l'effet des ondes sonores, la distance entre les armatures du condensateur change, ce qui entraîne une variation de la capacité du condensateur. On conclut en soulignant l'importance d'avoir des connaissances à la fois en mécanique et en électricité pour comprendre le fonctionnement du microphone.

Le lancer de gerbe de paille (3)

Dans cet exercice, on étudie l'intensité sonore émise par une enceinte et les limites d'exposition auxquelles il faut se conformer. Le cours commence par expliquer que l'enceinte émet des ondes sonores de manière isotrope, c'est-à-dire qu'elle émet la même quantité d'énergie dans toutes les directions. L'intensité sonore mesurée dépend de la distance à la source. La relation donnée est I = P / (4πd²), avec I en watts par mètre carré, P en watts et d en mètres. Le cours introduit ensuite le niveau d'intensité sonore L qui est lié à l'intensité sonore par la relation L = 10 * log(I / I0), avec L exprimé en décibels, I en watts par mètre carré et I0 en watts par mètre carré. On apprend que le microphone est relié par un amplificateur à l'enceinte. L'intensité sonore mesurée à un mètre de l'enceinte est donnée (I1 = 3,2 * 10^-3 W/m²). La première question demande de calculer le niveau d'intensité sonore correspondant à cette intensité (L1). En utilisant la relation donnée, on trouve que L1 = 95 décibels. Ensuite, on nous présente les durées limites d'exposition journalière imposées par la législation européenne pour chaque niveau d'intensité sonore. La question 2 demande comment le résultat de la question 1 se situe par rapport à ces durées limites. En calculant les durées correspondantes, on constate que pour une intensité sonore de 95 dB, la durée limite est de 15 minutes par jour. La question 3 demande de trouver la puissance de l'enceinte (P) en utilisant la relation donnée. En remplaçant les valeurs connues (I1 et d1), on trouve P = 4,01 * 10^-2 W. Les organisateurs d'une manifestation sportive ont fixé une valeur maximale d'intensité sonore (2 * 10^-4 W/m²) pour protéger les spectateurs. La question suivante demande d'expliquer pourquoi cette valeur a été choisie. En utilisant la relation donnée, on trouve l'intensité sonore correspondante (Imax = 4 * 10^-4 W/m²). Enfin, il est question de la distance de sécurité entre les barrières et l'enceinte pour respecter la valeur maximale d'intensité sonore choisie par les organisateurs. En utilisant à nouveau la relation donnée, on trouve que la distance minimale à respecter est de 1,8 mètres. Étant donné que la distance entre les barrières et l'enceinte est de 3 mètres, les spectateurs ne seront pas exposés à un niveau d'intensité sonore qui pourrait causer des dommages graves. Le cours se termine en soulignant l'importance de bien connaître les relations données et de savoir manipuler les équations correspondantes.

La mission Grace-Fo (1)

Dans cette vidéo, Théobald de Studio explique la caractérisation de l'orbite d'un satellite, en se basant sur la mission GRAFO qui envoie deux satellites jumeaux sur la même orbite. Il mentionne que l'attraction gravitationnelle de la planète varie faiblement d'un mois à l'autre en raison d'une infime fraction de la masse terrestre en mouvement constant, ce qui entraîne des variations dans l'attraction gravitationnelle. Dans la première partie de la vidéo, Théobald se concentre sur la caractérisation de l'orbite des satellites. Il explique que l'orbite est quasi-circulaire, avec une altitude z de 490 km et une inclinaison de 89° par rapport à l'équateur. Il mentionne également que les satellites sont situés à une distance L l'un de l'autre. Il présente ensuite les forces qui s'appliquent sur les satellites, en se concentrant sur le mouvement d'un seul satellite pour l'instant. Dans une question, il demande de faire un schéma montrant la Terre, le rayon RT et le satellite situé sur son orbite à une altitude z. Il explique ensuite l'expression vectorielle de la force gravitationnelle F de T sur S exercée par la Terre sur le satellite. Il utilise une formule qui comprend la masse de la Terre, la masse du satellite et la distance entre la Terre et le satellite. Il conclut que la force gravitationnelle est attractive et doit être dirigée vers la Terre. Ensuite, il demande d'en déduire l'expression du champ vectoriel terrestre G. Il utilise la relation entre la force gravitationnelle et le champ gravitationnel pour trouver cette expression. Dans une autre question, il demande d'établir l'expression vectorielle de l'accélération a du satellite en considérant uniquement l'action de la Terre. Il utilise le principe fondamental de la dynamique pour trouver cette expression. Enfin, il demande de montrer que dans le cadre de l'approximation d'une orbite circulaire, le mouvement du satellite est uniforme. Il suppose l'orbite circulaire et explique que dans ce cas, le mouvement est uniforme si la vitesse est constante. Il décompose l'accélération en accélération tangentielle et accélération normale et utilise cette décomposition pour montrer que la vitesse est constante dans le cas d'un mouvement circulaire. La vidéo se termine ici, mais Théobald encourage les spectateurs à poser des questions dans les commentaires.

La mission Grace-Fo (1)

Dans cette vidéo, Théobald de Studio aborde la caractérisation de l'orbite d'un satellite dans le cadre de la mission GRAFO. Il explique que cette mission envoie deux satellites jumeaux sur la même orbite. L'attraction gravitationnelle de la planète varie légèrement d'un mois à l'autre en raison d'une fraction infime de la masse terrestre constamment en mouvement. Cela peut rendre l'attraction gravitationnelle tantôt centripète, tantôt non centrée. Dans la première partie de la vidéo, Théobald se concentre sur la caractérisation de l'orbite. Il mentionne que l'orbite des satellites de cette mission est quasi-circulaire, à une altitude de 490 km et avec une inclinaison de 89° par rapport à l'équateur. Il note également que les deux satellites sont situés à une distance l l'un de l'autre. Il explique ensuite les forces qui s'appliquent aux satellites, en se concentrant sur le mouvement d'un seul satellite pour l'instant. On lui demande de faire un schéma montrant la Terre, le rayon RT et le satellite situé sur son orbite à une altitude z. Il indique que la force gravitationnelle exercée par la Terre sur le satellite peut être représentée par le vecteur n dirigé du satellite vers la Terre. Il donne ensuite l'expression vectorielle de cette force, qui dépend de la masse de la Terre, de la masse du satellite et de la distance entre la Terre et le satellite, portée par le vecteur n. Il rappelle que cette force est attractive et donc dirigée dans le sens de n. Il poursuit en déduisant l'expression du champ gravitationnel terrestre, puisque la force gravitationnelle et le champ gravitationnel sont reliés. Cette expression dépend de la masse de la Terre, de la masse du satellite, de la distance entre la Terre et le satellite et est portée par le vecteur n. Ensuite, Théobald établit l'expression vectorielle de l'accélération du satellite en considérant uniquement l'action de la Terre. Il définit le système comme étant le satellite de masse m et de centre de masse S, et le référentiel comme étant géocentrique supposé galiléen. Utilisant le principe fondamental de la dynamique, il montre que la somme des forces extérieures est égale à la masse du satellite multipliée par son accélération. En utilisant l'expression de la force gravitationnelle précédemment calculée, il trouve l'expression de l'accélération du satellite, qui dépend du champ gravitationnel, de la masse du satellite, de la distance entre la Terre et le satellite et est portée par le vecteur n. Enfin, il montre que dans le cadre de l'approximation d'une orbite circulaire, le mouvement du satellite est uniforme. Pour cela, il suppose que l'orbite est circulaire et montre que si c'est le cas, le mouvement du satellite est uniforme, ce qui signifie que sa vitesse est constante. Il utilise la décomposition de l'accélération en accélération tangentielle et accélération normale pour montrer que dans ce cas, l'accélération du satellite est uniquement selon le vecteur unitaire n. Cela signifie que le terme de la dérivée de la vitesse par rapport au temps est nul, ce qui entraîne que la vitesse du satellite est constante et donc que son mouvement est uniforme. Théobald conclut cette première partie de l'exercice et invite les spectateurs à poser des questions en commentaire.

La mission Grace-Fo (2)

Dans cette vidéo, Théobald de Sudéo poursuit l'étude du mouvement d'un satellite autour de la Terre. Il rappelle que dans la vidéo précédente, ils ont étudié le mouvement circulaire uniforme du satellite sur une orbite circulaire. Maintenant, ils doivent montrer que l'expression de la vitesse du satellite peut être exprimée comme GMt divisé par RT plus Z. Théobald explique qu'ils ont l'expression de l'accélération du satellite, qui comprend GMt divisé par RT plus Z, où G est la masse de la Terre et RT est le rayon de la Terre. Il souligne également que dans un mouvement circulaire uniforme, l'accélération est uniquement portée par le vecteur normal, qui est dirigé vers le centre de la Terre. Il n'y a pas d'accélération tangentielle en raison de la nature uniforme du mouvement. Ainsi, la vitesse du satellite au carré peut être exprimée comme GMt divisé par RT plus Z. Ensuite, Théobald aborde la question de la révolution du satellite. Il explique que la période de révolution correspond au temps qu'il faut au satellite pour faire le tour de la Terre. Il utilise la formule de la distance parcourue divisée par la vitesse constante du satellite pour trouver la période de révolution. En substituant la valeur de la vitesse du satellite dans la formule, il obtient une période de révolution de 5653 secondes, soit environ 1h34. Il conclut que le satellite fait environ 15,3 fois le tour de la Terre en une journée, ce qui est cohérent avec les informations fournies. Ensuite, Théobald aborde une situation particulière où deux satellites sont impliqués. Il explique que le premier satellite survole une zone où le champ gravitationnel n'est pas centripète, tandis que le deuxième satellite survole une zone où le champ gravitationnel est centripète. La question posée est de savoir si la distance entre les deux satellites restera constante. Théobald commence par étudier le deuxième satellite, qui suit un mouvement circulaire uniforme. Son accélération est seulement portée par le vecteur normal, et sa vitesse est constante. En revanche, le premier satellite subit un champ gravitationnel qui comporte à la fois une composante normale et une composante tangentielle. Sa vitesse n'est pas constante et il subit un mouvement circulaire accéléré. Théobald explique que dans ce cas, la distance entre les deux satellites augmentera, car le premier satellite accélère tandis que le deuxième satellite maintient une vitesse constante. Théobald conclut en encourageant les spectateurs à poser des questions et annonce une prochaine vidéo.

La mission Grace-Fo (3)

Dans cette vidéo, Théobald de Studio explique le principe de l'interféromètre embarqué utilisé dans la mission GRASFO, qui consiste à mesurer la distance entre deux satellites jumeaux situés sur la même orbite pour étudier les changements du champ gravitationnel terrestre. Pour cela, un laser est envoyé sur un miroir semi-réfléchissant, séparant ainsi le laser en deux parties. L'interféromètre permet de détecter les interférences entre ces deux sources cohérentes pour mesurer la distance entre les satellites. La différence de marche entre les chemins optiques est calculée en fonction de la longueur d'onde et de la distance entre les miroirs. En montrant que la variation de distance entre les satellites correspond à deux états successifs d'interférence constructive, il est démontré que la plus petite variation de distance détectable par l'interféromètre est de 532 nanomètres, ce qui est très précis.

La mission Grace-Fo (4)

Dans cette vidéo, Théobald de Studio nous explique le fonctionnement d'un accéléromètre utilisé dans le cadre de la mission Grasse-Faux. L'accéléromètre permet d'accéder au champ gravitationnel terrestre en mesurant les forces non gravitationnelles. L'accéléromètre est composé d'une masse d'épreuve située au centre d'une cage électrostatique. Cette masse subit un déplacement lorsque soumise à une force non gravitationnelle, ce qui modifie la capacité des trois paires de condensateurs. Dans cette étude, on se concentre sur un condensateur plan avec une armature mobile à gauche et une armature fixe. Une tension U est appliquée entre les deux armatures. L'influence du déplacement X, choisi comme positif, sur la capacité C du condensateur est discutée. La capacité C est inversément proportionnelle à X, donc si X augmente, C diminue. L'expression du champ électrique E entre les plaques du condensateur est déterminée en fonction de U, E, X et du vecteur unitaire i. On rappelle que le champ électrique entre deux plaques parallèles a pour norme U/D et est dirigé de la plaque positive vers la plaque négative. Ainsi, E est égal à U/(E+X) et est porté par le vecteur unitaire i. L'armature mobile est soumise au champ E1 créé par l'armature fixe. Selon les lois de l'électrostatique, E1 est égal à E/2. La force mécanique subie par l'armature mobile, modélisée par F, est opposée à E. Parmi les quatre schémas proposés, le deuxième représente correctement le champ électrique E et la force électrique F car E va du plus vers le moins et F est opposée à E. Dans la dernière question, on explique que le condensateur est associé à un deuxième condensateur et que la masse d'épreuve est mobile entre les deux armatures fixes. Les forces électrostatiques exercées par les deux armatures fixes se compensent, donc leur somme est nulle. Cela entraîne que les champs électriques EG à gauche et ED à droite sont égaux. Ainsi, la relation entre les champs électriques EG et ED est que EG = ED. Ce cours explique donc le fonctionnement d'un accéléromètre dans le contexte de la mission Grasse-Faux et comprend des explications sur la capacité du condensateur, le champ électrique et les forces électriques.

Protection des fondations en acier des éoliennes en mer (1)

Dans cette vidéo, Théobald du Studio explique la protection des éoliennes en mer contre la corrosion. Deux méthodes principales sont utilisées : l'anode sacrificielle et la protection par courant imposé. Dans cet exercice, il se concentre sur la protection cathodique avec une anode sacrificielle en aluminium. Il cherche à vérifier si le fer peut être protégé de l'oxydation en le mettant en contact avec de l'aluminium. La réaction qui modélise cette transformation est 2Al + 3Fe2+ -> 3Al2+ + 3Fe. Le quotient de réaction initial est exprimé en fonction des concentrations en ions Al3+ et Fe2+, et sa valeur est calculée. Grâce à la comparaison de ce quotient avec la constante d'équilibre, on détermine que la réaction se fait dans le sens direct. La réaction à l'électrode d'aluminium est décrite comme l'oxydation de l'aluminium solide en ions Al3+. L'intensité électrique négative indiquée sur le schéma est cohérente avec cette réponse. Enfin, l'électrode d'aluminium est identifiée comme l'anode dans la pile. Dans la prochaine vidéo, Théobald continuera à expliquer comment protéger les éoliennes et déterminer la quantité d'aluminium nécessaire.