Cours d'apprentissage en ligne

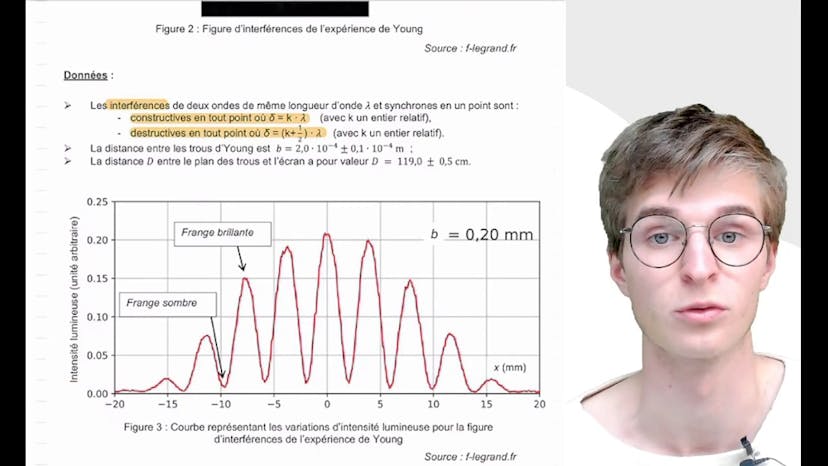
Trous d'Young (1)

Dans cette vidéo, nous abordons l'expérience des trous de Yong en physique. L'objectif est d'envoyer un laser sur un dispositif de trous de Yong, où le laser peut passer par deux trous spécifiques. Les deux ondes qui résultent de cela interagissent et créent une figure d'interférence sur un écran situé à une distance D beaucoup plus grande que la distance B entre les deux trous. Grâce à cette figure d'interférence, on peut déterminer la longueur d'onde du laser utilisé. La première question consiste à justifier que la différence de marche delta peut être assimilée à S2M moins S1M, dans le cas où le milieu traversé par les ondes lumineuses est l'air. En remplaçant N milieu par NR, où NR est l'indice de réfraction de l'air (qui vaut 1), on obtient que delta vaut NR S2M moins S1M, équivalent à S2M moins S1M. Ainsi, l'indice de réfraction de l'air étant toujours égal à 1, cela simplifie les calculs en optique. En utilisant le théorème de Pythagore dans les triangles S1O1M et S2O2M de la figure 1, on peut exprimer S1M² et S2M² en fonction de D, X et B sur 2. Pour S1M², on obtient D² plus X moins B sur 2 au carré et pour S2M², on obtient D² plus X plus B sur 2 au carré. Il est admis que lorsque D est très grand par rapport à B, on peut montrer que S2M² moins S1M² vaut 2DΔ. En utilisant cette relation, on peut en déduire que la différence de marche Δ peut s'écrire comme Δ = X fois B divisé par D. Ensuite, la vidéo aborde la figure d'interférence obtenue sur l'écran et explique que les interférences des deux ondes sont constructives lorsque Δ est égal à k fois λ (avec k un entier et λ la longueur d'onde) ou destructives lorsque Δ est égal à k plus 1 demi fois λ. En admettant que Δ vaut XB sur D, il est ensuite montré que X vaut kλD sur B pour les points où M est situé à un maximum d'intensité d'une frange brillante. En résumé, l'expérience des trous de Yong consiste à envoyer un laser sur un dispositif de trous où les interférences des ondes résultantes créent une figure d'interférence. En utilisant le théorème de Pythagore, on peut établir des relations entre les différentes distances dans le dispositif. Les interférences sont soit constructives, soit destructives en fonction de la différence de marche Δ, qui peut être exprimée comme Δ = XB sur D. Finalement, la distance X est égale à kλD sur B pour les points où M est situé à un maximum d'intensité d'une frange brillante.

Trous d'Young (2)

Dans cette vidéo, nous examinons la fin de l'exercice sur le dispositif des trous de Yonk. Nous essayons de déterminer la longueur d'onde du laser utilisé pour cette expérience à partir de la figure d'interférence observée. En utilisant la formule X = KλD/B, nous dérivons l'expression de l'interfrange Y en fonction de λB et D. L'interfrange représente la distance entre deux franges sombres ou claires. Dans notre cas, puisque X se situe sur une frange claire lors d'une interférence constructive, nous prenons deux franges claires successives notées K+1 et K pour déterminer Y, qui est égal à λD/B. À l'aide de la figure 3, nous mesurons graphiquement 8 Y, ce qui correspond à une distance de 30mm. En divisant cette distance par le nombre de périodes mesurées, nous obtenons une valeur de 3,9 mm pour l'interfrange Y. En utilisant la formule Y = λD/B, nous déduisons que λ vaut environ 660 nm. Ensuite, nous devons identifier les lasers qui ont pu être utilisés dans cette expérience parmi plusieurs options (laser bleu, vert, rouge A, B ou C). Étant donné les incertitudes présentes dans l'expérience, nous devons prendre en compte ces incertitudes pour calculer U de lambda, qui représente l'incertitude sur lambda. En utilisant les valeurs données dans l'énoncé et en effectuant les calculs nécessaires, nous obtenons une incertitude U de lambda de 4x10^-8 mètres. Finalement, nous pouvons conclure que tous les lasers ayant une longueur d'onde comprise entre 620 et 700 nm ont pu être utilisés dans cette expérience. Cela inclut le laser rouge A (630 nm), le laser rouge B (650 nm) et le laser rouge C (694 nm). Nous ne sommes pas en mesure de distinguer plus précisément quel laser a été utilisé dans cette expérience en utilisant nos instruments de mesure.

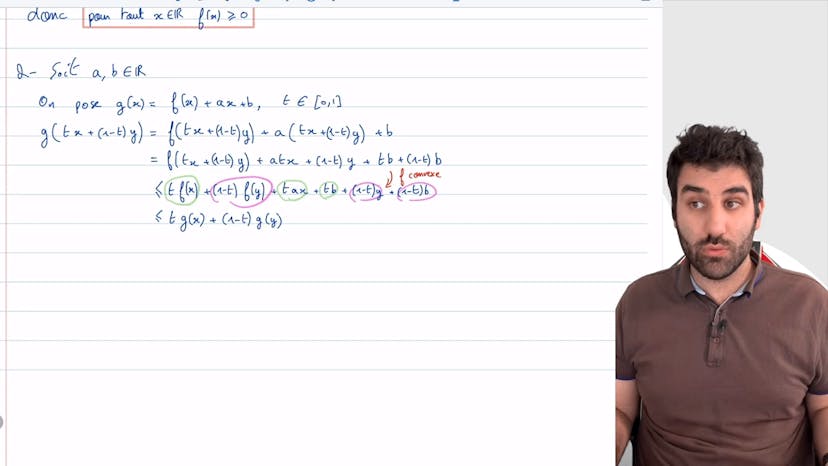
HM Test

Dans cet exercice, nous utilisons principalement l'inégalité des pentes pour démontrer certains résultats. Tout d'abord, on suppose que la limite de la fonction f quand x tend vers l'infini est égale à 0 et l'objectif est de montrer que f est positive. Pour cela, on fait un raisonnement par l'absurde en supposant qu'il existe un x0 tel que f(x0) est strictement négatif. En utilisant la définition de la limite, on montre qu'il existe un x1 plus grand que x0 tel que f(x1) est entre f(x0) et 0. En utilisant l'inégalité des pentes, on montre ensuite que f(x) doit être strictement plus grand que f(x1), ce qui contredit la limite de f qui est égale à 0. Donc, on conclut que f ne peut pas être négative et donc pour tout x, f(x) est supérieur ou égal à 0. Ensuite, on nous demande de montrer que la somme d'une fonction convexe et d'une fonction affine est convexe. Pour cela, on considère une fonction g qui est la somme d'une fonction convexe f et d'une fonction affine ax + b. On veut montrer l'inégalité de convexité, c'est-à-dire que g(tx + (1-t)y) est inférieur ou égal à t*g(x) + (1-t)*g(y) pour tout t entre 0 et 1. En remplaçant g par son expression, on simplifie l'expression et on utilise la convexité de f pour montrer que g(tx + (1-t)y) est inférieur ou égal à t*f(x) + (1-t)*f(y). On regroupe les termes qui nous intéressent et on conclut que g est convexe. Enfin, on suppose que la courbe représentative de f admet une asymptote et on souhaite montrer que la courbe est toujours au-dessus de cette asymptote. On pose y = x + b comme équation de l'asymptote de f et on définit g(x) comme la différence entre f(x) et ax + b. On utilise le principe de l'asymptote pour montrer que la limite de g(x) quand x tend vers l'infini est égale à 0. En utilisant la question précédente, on conclut que g est une fonction convexe et comme sa limite est égale à 0, g est positive. Cela signifie que pour tout x, f(x) est supérieur ou égal à ax + b, ce qui montre que la courbe de f est toujours au-dessus de son asymptote. En résumé, nous avons démontré trois résultats dans cet exercice. Tout d'abord, si la limite de f en l'infini est égale à 0, alors f est positive. Ensuite, la somme d'une fonction convexe et d'une fonction affine est convexe. Enfin, si la courbe représentative de f admet une asymptote, alors la courbe est toujours au-dessus de cette asymptote.

Télémètre à ultrasons (1)

Bonjour à tous ! Aujourd'hui, on va étudier les incertitudes à travers le télémètre à ultrasons. Cet exercice de physique a été donné l'année dernière au bac en Asie. Le télémètre à ultrasons permet de déterminer la position d'un objet en envoyant des ultrasons qui se réfléchissent sur l'objet et reviennent vers le récepteur. En mesurant la durée delta-t de parcours des ultrasons et en connaissant la vitesse de propagation d'un ultrason dans l'air, on peut calculer la distance séparant le télémètre de l'objet, et donc la position de l'objet. Dans cet exercice, on suppose que l'émetteur et le récepteur sont sur le même axe et que les ultrasons se déplacent uniquement sur cet axe. Pour trouver la relation entre la distance X et la durée delta-t, on utilise la formule X = (Vitesse x Delta-t) / 2. Dans le programme Python présenté, on calcule cette distance en multipliant la vitesse par la durée mesurée, divisée par 2. La vitesse des ultrasons dans l'air dépend de la température, il faut donc calibrer le télémètre avant de l'utiliser. Pour cela, on mesure plusieurs distances connues X0 et les durées correspondantes Delta-t0 fournies par l'ordinateur. On peut alors calculer la vitesse Vs0. En répétant ces mesures pour différentes distances, on obtient plusieurs vitesses Vs. En faisant la moyenne de toutes ces vitesses, on peut calibrer le télémètre. Dans la prochaine vidéo, on abordera le calcul des incertitudes et les méthodes de mesure d'incertitude. N'hésitez pas à poser vos questions en commentaire.

Télémètre à ultrasons (2)

Bonjour à tous ! Dans cette vidéo, nous poursuivons la correction de l'exercice sur le télémètre à ultrasons et les incertitudes de mesure. Dans la première partie, nous avons présenté un protocole expérimental pour déterminer la vitesse des ultrasons (VS). Maintenant, nous utilisons un autre protocole où l'obstacle est toujours placé au même endroit et où nous mesurons le Δt correspondant à chaque mesure. À partir de Δt, nous mesurons VS plusieurs fois afin d'obtenir une moyenne et une valeur précise de VS. Nous utilisons également des concepts d'incertitude pour améliorer notre mesure. La méthode est similaire à celle proposée précédemment, mais nous nous plaçons toujours à la même distance et calculons manuellement la VSI pour chaque XI et Δti. Ensuite, nous mesurons VSI plusieurs fois pour éviter les problèmes d'incertitude et calculons la moyenne. Maintenant, nous devons calculer la valeur moyenne de VS en utilisant des incertitudes et des chiffres significatifs appropriés. Nous utilisons la formule VS = VS moyen ± incertitude de type A, où l'incertitude de type A (σ) est donnée par σ/√n (n = nombre de mesures, σ = incertitude donnée par la calculatrice). Dans notre cas, la valeur moyenne de VS est de 349,4 m/s ± 0,9 m/s. Les chiffres significatifs de la moyenne et de l'incertitude doivent être les mêmes, dans ce cas, nous nous arrêtons au dixième. Passons maintenant à la question suivante, où nous devons modifier une ligne de code Python pour tenir compte de la valeur moyenne de VS. Ensuite, nous abordons la question de la mesure de la distance x avec les incertitudes associées. Pour cela, nous utilisons la formule x = x mesuré + incertitude de calcul de x. L'incertitude de calcul de x est basée sur les incertitudes de mesure de Δt et de VS. Après avoir fait les calculs, nous obtenons x = 6,0 cm ± 0,1 cm. Il est important que l'incertitude et le résultat soient exprimés dans la même unité pour une cohérence. En conclusion, nous avons terminé la partie sur les incertitudes et nous poursuivrons avec la deuxième partie de cet exercice. N'hésitez pas à poser vos questions en commentaire.

Télémètre à ultrasons (3)

Dans cette vidéo, Obel2Studio corrige un exercice de mécanique sur la suite du télémètre d'ultrasons, issu du BAC. Le système étudié est composé d'une voiture lâchée sans vitesse initiale qui descend une pente inclinée d'un angle alpha. Le système est soumis au poids, à la réaction du support et à des forces de frottement opposées au mouvement. Dans la première partie de la vidéo, Obel2Studio explique la direction et le sens du vecteur accélération de la voiture. Il montre que la direction est vers les X positifs et que le sens est négatif, car la voiture descend les X. Ensuite, il énonce la deuxième loi de Newton, qui est le principe fondamental de la dynamique. Ce principe dit que la somme des forces extérieures appliquées sur un système est égale à la dérivée du vecteur quantité de mouvement par rapport au temps. Si la masse du système est constante, cela se simplifie en disant que la somme des forces extérieures est égale à la masse multipliée par l'accélération. Obel2Studio utilise ensuite ce principe pour établir l'équation horaire du mouvement du centre de masse du système. Il montre que la vitesse est donnée par moins ft/m fois t et que la position est donnée par moins un demi ft^2/m plus x0. 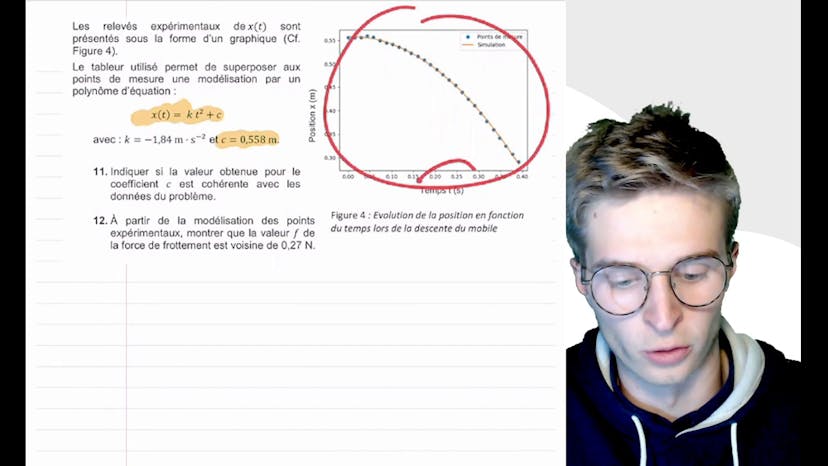Dans la partie suivante de la vidéo, Obel2Studio présente les relevés expérimentaux de la position en fonction du temps et montre une modélisation polynomial de ces relevés. Il explique que la valeur du coefficient c dans cette modélisation est cohérente avec les données du problème, car elle correspond à x0, la position initiale de la voiture. Enfin, Obel2Studio utilise la modélisation des points expérimentaux pour montrer que la valeur de la force de frottement est proche de 0,27 N. Il utilise l'expression de la résultante des forces pour exprimer la force de frottement en fonction des autres valeurs connues et fait une application numérique pour trouver la valeur de la force de frottement. La vidéo se termine en annonçant la suite de l'exercice dans une prochaine vidéo et en encourageant les auditeurs à poser des questions s'ils en ont.

Télémètre à ultrasons (4)

Dans cette vidéo, Théobald de Studio effectue une étude énergétique sur un exercice de mécanique. Il commence par rappeler le théorème de l'énergie cinétique entre les positions A et B, qui déclare que la variation de l'énergie cinétique entre ces deux points est égale à la somme des travaux des forces exercées sur l'objet. Théobald développe ensuite cette équation en fonction des forces exercées : la force de frottement et le poids. Il explique également que la réaction du support, étant normale au mouvement, ne produit pas de travail. Ensuite, Théobald utilise le théorème de l'énergie cinétique pour calculer la valeur de la force de frottement. À l'aide des données sur la position du centre de masse, il obtient la vitesse du centre de masse au point B, qui est de 1,21 m/s. En utilisant cette valeur, il trouve une nouvelle estimation de la force de frottement, qui est de 0,29 N. Enfin, Théobald partage une astuce pour calculer rapidement le produit scalaire entre deux vecteurs. Si l'angle est présent entre les deux forces et qu'elles tirent dans le même sens, le produit scalaire est égal à la norme de chaque vecteur multipliée par le cosinus de l'angle, avec un plus devant. Si les forces ne tirent pas dans le même sens, le produit scalaire est le produit des normes multiplié par le sinus de l'angle, avec un moins devant. Cette astuce peut aider à gagner du temps et à éviter les erreurs de calcul. Théobald conclut en encourageant les spectateurs à poser des questions dans les commentaires s'ils en ont.

L’acide formique pour stocker le dihydrogène (1)

Dans cette vidéo, Théobald de Cydéo explique comment utiliser l'acide formique pour stocker du dihydrogène. L'objectif est de remplacer l'essence dans les moteurs à explosion, car le dihydrogène est inflammable à température ambiante, rendant son stockage difficile. Pour résoudre ce problème, on peut réagir le dihydrogène avec du dioxyde de carbone pour former de l'acide formique, qui est peu inflammable. Les chercheurs de l'université de Rice ont trouvé un procédé catalytique pour produire de l'acide formique. Ensuite, Théobald explique comment justifier que l'acide formique est également appelé acide métanoïque dans la nomenclature officielle. En dessinant la formule semi-développée de l'acide, il identifie le groupe carboxylique comme le groupe fonctionnel principal, ce qui donne la fonction "acide carboxylique" et la terminaison "acide métanoïque" selon la nomenclature UPAC. Ensuite, il examine comment vérifier qu'un litre de dihydrogène à une pression de 300 bars et à une température de 25°C contient une masse de 28g de dihydrogène, en utilisant l'équation des gaz parfaits (PV = nRT). En appliquant cette équation avec les unités appropriées, il établit que la masse de dihydrogène est de 28g dans les conditions données. Il explique ensuite comment vérifier qu'un litre d'acide formique peut produire 53g de dihydrogène, comme indiqué dans un document. Il utilise la quantité de matière d'acide formique introduite au départ et montre que la quantité de dihydrogène formé à la fin de la réaction est égale à la quantité d'acide formique initialement présente. En utilisant la masse molaire du dihydrogène et la quantité de matière d'acide formique, il calcule que la masse de dihydrogène est effectivement de 53g dans les conditions données. Enfin, Théobald mentionne deux avantages de l'acide formique par rapport au stockage de dihydrogène sous pression. Tout d'abord, l'acide formique est peu inflammable à pression et température ambiante, contrairement au dihydrogène. De plus, l'utilisation de l'acide formique permet une plus grande capacité de stockage par rapport au gaz sous pression. Pour toute question, Théobald encourage les spectateurs à les poser en commentaire, et il se propose d'y répondre avec plaisir dans la suite de l'exercice.

L’acide formique pour stocker le dihydrogène (2)

Dans cette vidéo, Théobald de Cidéo explique une méthode conductimétrique utilisée pour contrôler la teneur en acide formique d'une solution aqueuse. L'exercice est issu du baccalauréat de l'année dernière. Dans la première partie, il est mentionné que l'acide formique est une bonne solution pour stocker le dihydrogène. L'objectif ici est de contrôler la concentration en acide formique d'une solution préparée par des chercheurs de l'Université de Reuss. Ils ont dilué 100 fois une solution S0 d'acide formique pour obtenir une solution S1 de concentration C1. Un volume V1 de cette solution est prélevé pour mesurer sa conductivité. Selon l'équation de réaction de l'acide formique avec l'eau, seuls les ions oxonium (H3O+) et les ions formiate (HCO-) contribuent à la conductivité. La conductivité sigma de la solution peut donc être exprimée en fonction des concentrations et des conductivités molaires ioniques de ces ions. On obtient ainsi la formule suivante : sigma = [H3O+] * lambda(H3O+) + [HCO-] * lambda(HCO-). 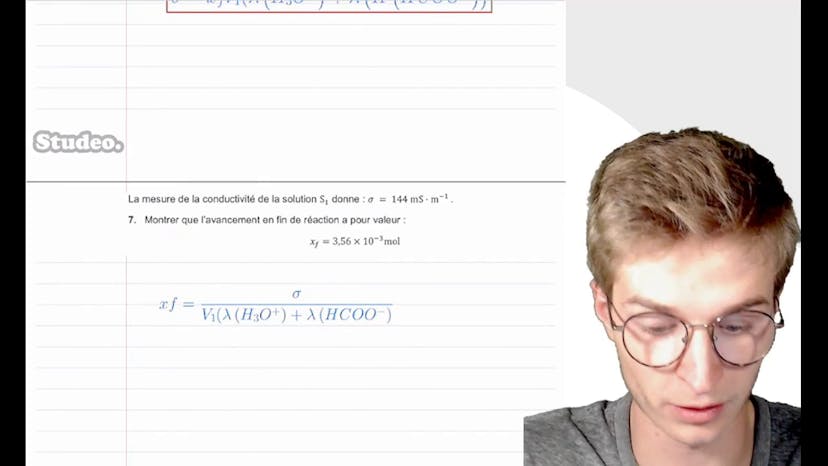En déduisant une relation entre sigma, lambda(H3O+), lambda(HCO-) et V1, ainsi qu'en utilisant la formule d'avancement de la réaction, on peut montrer que l'avancement en fin de réaction a pour valeur XF = 3,56 * 10^-3 mol. La mesure de la conductivité de la solution S1 donne une valeur de 144 mS/m. En utilisant la formule précédente pour isoler XF, on obtient XF = sigma / (V1 * lambda(H3O+) + V1 * lambda(HCO-)). La constante d'équilibre Ka peut être écrite en fonction de XF grâce à la formule: Ka = (XF/V1)^2 * (1/C*). La concentration standard C* est de 1,00 mol/L. En isolant C1 dans cette équation, on obtient C1 = (XF^2/V1^2) * (1/(C* * Ka)). En utilisant les valeurs numériques disponibles, on trouve que C1 = 7,16 * 10^-2 mol/L. Pour déterminer la concentration de la solution mère (S0), on observe qu'elle est diluée 100 fois pour obtenir S1. Ainsi, C0 = 100 * C1. On trouve donc que C0 = 7,16 mol/L. Enfin, on compare qualitativement cette concentration à la teneur en acide formique mentionnée dans l'article du document 2. L'article mentionne une solution aqueuse contenant 30% en masse d'acide formique, soit 7,0 mol/L. Les résultats obtenus sont donc en accord avec ceux mentionnés dans le document 2. Cet exercice est ainsi résumé de manière SEO friendly en mettant en avant les principaux concepts abordés tels que la conductivité, l'avancement de réaction, les concentrations et les constantes d'équilibre.

Savon de Marseille (1)

Dans cet exercice, nous étudions la saponification, qui est la réaction permettant de produire du savon. Plus précisément, nous nous intéressons à la synthèse organique du savon de Marseille en utilisant de l'huile d'olive et de la soude. Le cours commence par l'analyse du protocole expérimental fourni. L'huile d'olive utilisée est principalement constituée d'une espèce chimique appelée oléine, qui est un triester. Un triester est composé de trois groupes fonctionnels ester. En ce qui concerne la sécurité, l'utilisation de soude concentrée présente des risques, car elle est corrosive et peut causer des rougeurs, des brûlures et des irritations. Il est donc essentiel de suivre les règles de sécurité appropriées, notamment en travaillant sous une hotte aspirante pour éviter l'inhalation des vapeurs. Une des étapes du protocole consiste à ajouter de l'éthanol à la réaction. Bien que l'éthanol ne figure pas dans la réaction chimique, il est utilisé comme solvant pour permettre la réaction de l'oléine et de la soude, car ils ne peuvent pas réagir dans l'eau. Il est également demandé d'expliquer pourquoi l'ion oléate prédomine par rapport à l'acide oléique. Cela est dû au fait que la réaction produit une solution basique avec un pH supérieur au pKa de l'acide oléique. Ainsi, la base, sous forme d'ion oléate, prédomine par rapport à l'acide. Le chauffage de la réaction sert à accélérer la réaction en augmentant la température, qui est un facteur cinétique. Cela permet d'obtenir une vitesse de réaction plus élevée. Enfin, lors de la phase de relargage, il est expliqué pourquoi de l'eau salée est utilisée plutôt que de l'eau douce. L'eau salée favorise la séparation du glycérol et de l'oléate de sodium, car le glycérol est fortement soluble dans l'eau, tandis que l'oléate de sodium présente une faible solubilité avec l'eau. Ainsi, en utilisant de l'eau salée, on peut éliminer la plupart du glycérol de la phase aqueuse. Cet exercice aborde d'autres aspects de la saponification, mais ceux-ci sont les points principaux à retenir pour un résumé SEO friendly.

Savon de Marseille (2)

Bonjour à tous ! Aujourd'hui, nous allons parler de la réaction de saponification, qui permet d'obtenir du savon à partir d'un corps gras et de la soude. Dans cet exercice, nous cherchons à déterminer quel réactif est limitant. Nous connaissons les volumes et les concentrations des réactifs et nous devons calculer les quantités de matière initiales. Pour cela, nous utilisons les masses volumiques et les masses molaires des réactifs. Nous effectuons ensuite les calculs pour trouver les quantités de matière maximales de chaque réactif. En comparant ces quantités, nous pouvons déterminer que l'oléine est le réactif limitant. Ensuite, on nous demande pourquoi il est important d'éliminer le réactif en excès par lavage et quelle autre espèce chimique pourrait également être éliminée. Le réactif en excès est la soude, et il est corrosif. Par conséquent, il est essentiel de le laver pour éliminer tout excès. En utilisant de l'eau froide, nous pouvons également éliminer le glycérol, qui est soluble dans l'eau. 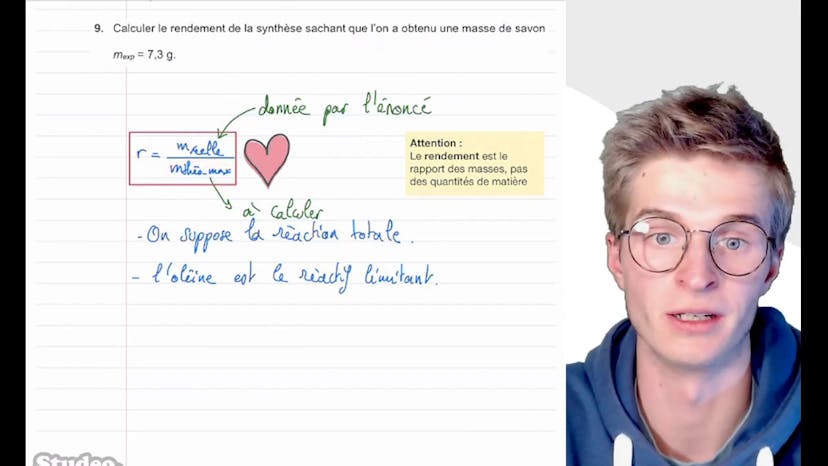Ensuite, nous devons calculer le rendement de la synthèse. Le rendement est le rapport entre la masse réelle obtenue (7,3 grammes) et la masse théorique attendue. Pour calculer la masse théorique, nous supposons une réaction totale et utilisons un tableau d'avancement pour trouver les quantités de matière finales. En utilisant les masses molaires, nous pouvons calculer la masse théorique maximale d'oléade de sodium. Finalement, nous divisons la masse réelle par la masse théorique pour obtenir un rendement de 0,80, soit environ 80%. Enfin, on nous demande de proposer une hypothèse pour expliquer pourquoi le rendement n'est pas de 100%. L'une des raisons peut être que la réaction n'est pas totale, ce qui est souvent le cas. Une autre explication pourrait être des erreurs de manipulation ou des pertes pendant la synthèse. J'espère que cela a été clair pour vous. N'hésitez pas à poser vos questions et bonnes révisions à tous ! Merci d'avoir regardé cette vidéo.