 Tous les sujets
Tous les sujets Maths
Maths Physique-Chimie
Physique-Chimie Corrigés de BAC
Corrigés de BAC Révisions Maths lycée
Révisions Maths lycée Prépa Examens
Prépa Examens
Terminale
Première
Seconde
MPSI/PCSI
2BAC SM Maroc
 Tous les sujets
Tous les sujets Maths
Maths Physique-Chimie
Physique-Chimie Corrigés de BAC
Corrigés de BAC Révisions Maths lycée
Révisions Maths lycée Prépa Examens
Prépa Examens
Corrigés de BAC
Bac Physique-Chimie
MPSI/PCSI

Dissolution d’une coquille d’oeuf (2)
Dans cette vidéo, Obald Studio examine la dissolution d'une coquille d'œuf dans du vinaigre. La coquille d'œuf est principalement composée de carbonate de sodium (CaCO3). L'expérience montre que la coquille se dissout progressivement dans le vinaigre. En utilisant des bandes d'absorption infrarouge, il est démontré que l'acide éthanoïque (CH3COOH) est présent dans ce processus. Une équation de réaction acido-basique est également présentée pour illustrer les réactions entre l'acide éthanoïque et les ions CO3- et HCO3-. En fin de compte, la réaction entre le vinaigre (acide éthanoïque) et le carbonate de calcium (CaCO3) produit des ions Ca2+, des ions CH3CO-, de l'eau (H2O) et du dioxyde de carbone (CO2). L'ion hydrogéno-carbonate (HCO3-) est qualifié d'espèce amphotère, car il peut être à la fois un acide et une base selon le couple chimique auquel il participe.
Corrigés de BAC
Bac Physique-Chimie
MPSI/PCSI
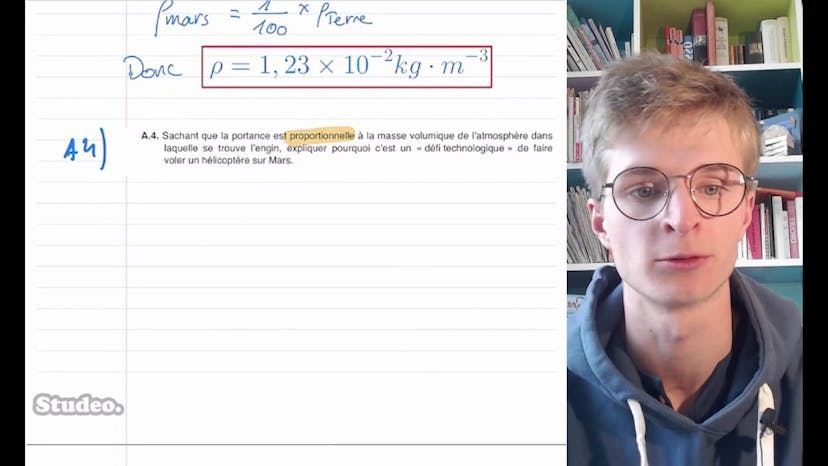
Ingenuity : le premier hélicoptère à voler sur Mars (1)
Dans cette vidéo, Théobald de Studio aborde la correction de la partie A de l'exercice 1 du BAC 2022 Nouvelle-Calédonie qui traite de la thermodynamique et de l'atmosphère sur Mars. Il explique que l'atmosphère peu dense de Mars pose des problèmes de portance pour le drone Ingenuity. Il introduit la loi des gaz parfaits (PV = nRT) et utilise les notions de masse volumique (ρ) et de masse molaire (M) pour montrer que la masse molaire de l'air sur Terre vaut RT/PM. Ensuite, il effectue des calculs numériques pour trouver la valeur de la masse volumique de l'air à 15°C. Il déduit que la masse volumique de l'atmosphère sur Mars est égale à 1% de celle de l'air sur Terre. Enfin, il explique pourquoi il est un défi technologique de faire voler un hélicoptère sur Mars en montrant que la portance est proportionnelle à la masse volumique, et donc diminue lorsque celle-ci diminue. Il conclut en indiquant que faire décoller un hélicoptère sur Mars est 100 fois plus difficile que sur Terre.
Corrigés de BAC
Bac Physique-Chimie
MPSI/PCSI
Ingenuity : le premier hélicoptère à voler sur Mars (2)
Dans cette vidéo, le professeur Théobald de Studio présente une résolution d'un problème ouvert en physique chimie, qui consiste à déterminer la valeur de la vitesse de rotation minimale des pales de l'hélicoptère Ingenuity sur Terre et sur Mars, afin que l'hélicoptère puisse décoller. Pour résoudre ce problème, le professeur propose une démarche en plusieurs étapes.
Tout d'abord, il explique que la portance minimale nécessaire à l'hélicoptère pour décoller doit compenser le poids de l'appareil. Il souligne que la portance et le poids sont deux forces, et que la portance minimale correspondra donc au poids de l'hélicoptère. Sachant que le poids dépend de l'intensité de pesanteur sur Terre et sur Mars, il faut d'abord trouver le poids de l'hélicoptère sur chaque planète.
Ensuite, le professeur utilise des graphiques représentant la portance en fonction de la vitesse de rotation des pales sur Terre et sur Mars. Il explique que chaque valeur de portance correspond à une vitesse de rotation des pales spécifique. Donc, pour trouver la vitesse de rotation minimale correspondant à la portance minimale, il faut utiliser ces graphiques.
Le professeur procède ensuite au calcul du poids de l'hélicoptère sur Terre et sur Mars, en utilisant les valeurs de masse de l'hélicoptère et les intensités de pesanteur fournies dans l'énoncé. Il obtient ainsi les valeurs de portance minimale sur Terre et sur Mars.
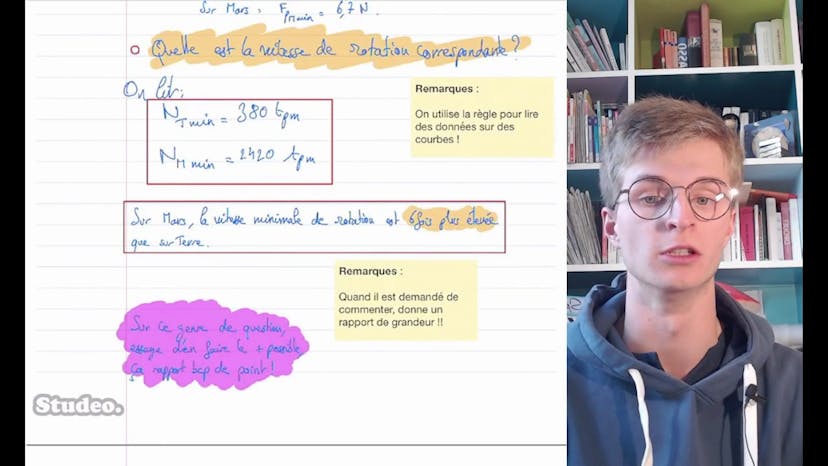
Enfin, le professeur lit les valeurs de vitesse de rotation minimales correspondantes sur les graphiques, en utilisant la règle pour lire les données. Il obtient ainsi les valeurs de vitesse de rotation minimales sur Terre et sur Mars.
Le professeur commente ensuite le résultat, en soulignant que la vitesse minimale de rotation sur Mars est 6 fois plus élevée que sur Terre. Il explique que cela met en évidence le défi technologique que représente le vol de l'hélicoptère sur Mars.
En conclusion, le professeur souligne l'importance d'essayer de résoudre le problème même si on n'obtient pas nécessairement un résultat final. Il rappelle que le cheminement et la démarche de résolution sont également évalués dans ce type de questions.
Corrigés de BAC
Bac Physique-Chimie
MPSI/PCSI
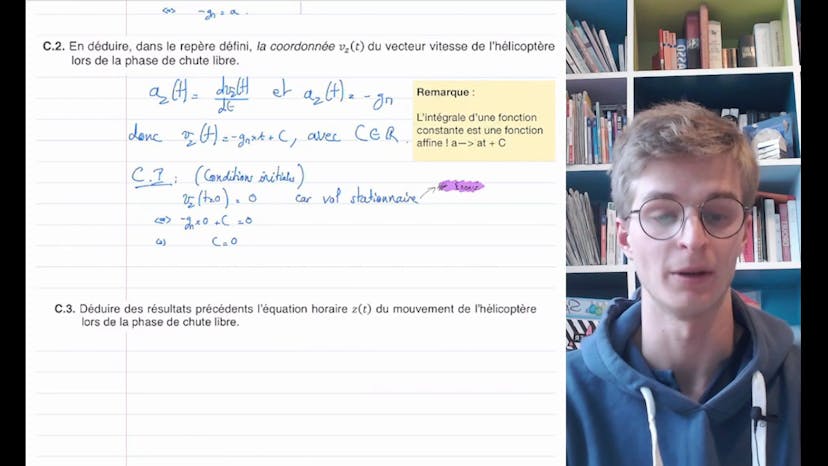
Ingenuity : le premier hélicoptère à voler sur Mars (3)
Dans cette vidéo, Théobald de Studio corrige la troisième partie du premier exercice de physique-chimie du bac de Nouvelle-Calédonie de 2022, qui porte sur la chute libre. L'exercice consiste à étudier la phase d'atterrissage d'un hélicoptère sur Mars. Lors de cette phase, l'hélicoptère cesse la propulsion à un mètre du sol et tombe en chute libre jusqu'au sol.
La première question demande d'appliquer la deuxième loi de Newton pour exprimer la coordonnée de l'accélération de l'hélicoptère lors de la chute libre. Pour cela, il faut faire un schéma de la situation, faire un bilan des forces et appliquer la deuxième loi de Newton. On obtient ainsi que l'accélération est égale à -GM, où G est le champ de pesanteur et M est la masse de l'hélicoptère.
Ensuite, on déduit la vitesse de l'hélicoptère en intégrant l'accélération par rapport au temps. On obtient que la vitesse est égale à -GMt.
Enfin, on détermine l'équation horaire du mouvement en intégrant la vitesse. On obtient que la position de l'hélicoptère en fonction du temps est égale à -1,5GMt^2 + H, où H est la hauteur initiale de l'hélicoptère.
On nous demande ensuite de déterminer la durée au bout de laquelle l'hélicoptère atteindra le sol. On résout l'équation de la position en fonction du temps en posant Z(t_sol) = 0, où t_sol est la durée de chute. On obtient ainsi que t_sol = racine de 2H/GM.
Ensuite, on calcule la vitesse de l'hélicoptère au moment de l'impact sur le sol en utilisant la valeur de t_sol dans l'expression de la vitesse. On obtient que la vitesse est égale à racine de 2GMH.
On nous dit que lors des essais préparatoires réalisés sur Terre, des vitesses d'impact de l'ordre de 16 km/h ont été enregistrées. On nous demande si le train d'atterrissage de l'hélicoptère est suffisamment résistant pour une utilisation sur Mars. On convertit la vitesse d'impact de 16 km/h en m/s ou on convertit la vitesse de l'hélicoptère en km/h. On compare les deux valeurs et on conclut que le train d'atterrissage est suffisamment résistant.
En conclusion, cette vidéo corrige la troisième partie d'un exercice sur la chute libre d'un hélicoptère lors de l'atterrissage sur Mars. La vidéo détaille les différentes étapes pour résoudre l'exercice, notamment l'application de la deuxième loi de Newton et l'intégration pour trouver la vitesse et la position de l'hélicoptère. On détermine ensuite la durée de chute et la vitesse d'impact pour conclure sur la résistance du train d'atterrissage.
Corrigés de BAC
Bac Physique-Chimie
MPSI/PCSI
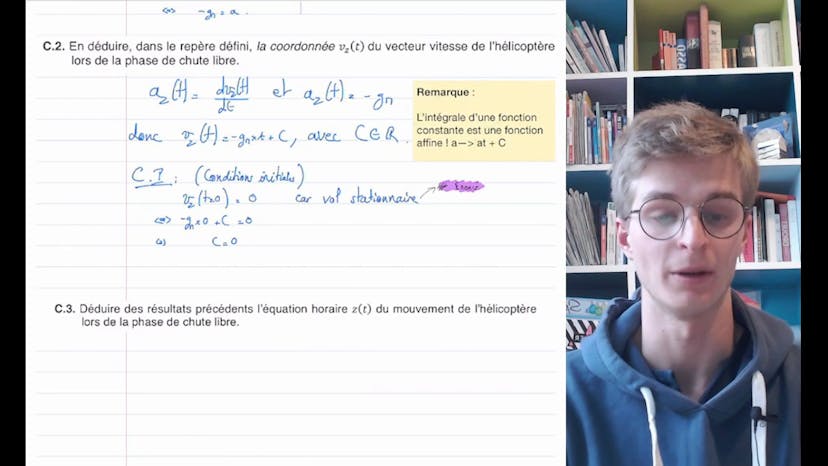
Ingenuity : le premier hélicoptère à voler sur Mars (4)
Bonjour à tous, dans cette vidéo, nous allons corriger ensemble la troisième partie du premier exercice de physique-chimie du bac de Nouvelle-Calédonie de 2022. Il s'agit de la phase d'atterrissage de l'hélicoptère Ingenuity sur Mars. La solution retenue est de cesser la propulsion à un mètre du sol et de laisser l'hélicoptère atteindre le sol en chute libre. La première question consiste à appliquer la deuxième loi de Newton afin d'exprimer l'accélération de l'hélicoptère lors de la chute libre. En faisant un schéma et un bilan des forces, on obtient l'équation AZ de T égale moins GM, où G est l'accélération due à la gravité et M est la masse de l'hélicoptère. En intégrant cette équation, on obtient la vitesse VZ de T égale moins GM fois T. En intégrant à nouveau, on trouve l'équation horaire du mouvement, Z de T égale moins 1,5 de GM T carré plus H, où H est la hauteur de départ de l'hélicoptère. En résolvant cette équation, on obtient la durée Tsol nécessaire pour que l'hélicoptère atteigne le sol, qui est égale à racine de 2H sur GM. En calculant cette durée, on obtient Tsol égale à 0,74 secondes. En utilisant cette durée, on peut calculer la vitesse Vsol de l'hélicoptère au moment de l'impact sur le sol, qui est égale à racine de 2GMH. En calculant cette vitesse, on trouve Vsol égale à 2,7 mètres par seconde. En comparant cette vitesse à celle des essais préparatoires sur Terre, on conclut que le train d'atterrissage est suffisamment résistant pour une utilisation sur Mars. Si vous avez des questions, n'hésitez pas à les poser en commentaire. À plus pour la suite !
Corrigés de BAC
Bac Physique-Chimie
MPSI/PCSI

Acide benzoïque (1)
Dans cette vidéo, Théobald de Cydéo présente un exercice de chimie sur la réaction de l'acide benzoïque avec l'eau dans le cadre du BAC de 2022 en Nouvelle-Calédonie. Il explique que l'exercice fait partie des trois exercices au choix et que les étudiants doivent en choisir deux.
Théobald recommande de survoler les données fournies, qui incluent les valeurs de pK des acides et bases, la solubilité de l'acide benzoïque et la masse molaire des différentes entités chimiques.
La première partie de l'exercice porte sur le calcul de la masse nécessaire pour préparer une solution d'acide benzoïque. Théobald rappelle que la concentration molaire est égale à N/V, avec V en litres et N en moles. En utilisant cette formule, il calcule la quantité de matière correspondant à la masse donnée et en déduit la masse nécessaire pour préparer la solution.
Ensuite, Théobald examine la saturation de la solution. Il explique que la solubilité maximale de l'acide benzoïque est donnée et que la solution est saturée si la concentration d'acide est égale à cette valeur. En vérifiant cette condition, il conclut que la solution n'est pas saturée.
L'équation de réaction de l'acide benzoïque avec l'eau est ensuite écrite. Théobald explique que l'acide réagit avec l'eau pour former l'ion benzoate et l'acide H3O+. Il vérifie que l'équation est équilibrée et que tous les réactifs et produits sont présents.
Théobald procède ensuite à la construction du diagramme de prédominance du couple acide benzoïque/ion benzoate. Il rappelle la relation entre le pH et le pKa et indique que la solution est dans le domaine de prédominance de l'acide, en se référant à la valeur du pH donnée.
Le tableau d'avancement est ensuite complété en fonction des concentrations initiales et finales. Théobald utilise l'équation de réaction pour remplir le tableau et calcule la quantité d'acide restante. L'avancement maximal est également calculé en considérant que tout l'acide a réagi pour former l'ion benzoate.
Enfin, Théobald montre que le taux d'avancement final s'écrit taux = [H3O+] à l'équivalence / C0 en utilisant les valeurs calculées précédemment. Il conclut que le taux d'avancement est faible, ce qui est cohérent avec le fait que la réaction a peu eu lieu.
Théobald termine en proposant de répondre aux questions des spectateurs et annonce qu'il continuera l'exercice dans une autre vidéo.
Corrigés de BAC
Bac Physique-Chimie
MPSI/PCSI

Acide benzoïque (1)
Dans cette vidéo, Théobald de Cydéo corrige un exercice de synthèse de l'acide benzoïque du BAC de l'année précédente. Le processus de synthèse se fait en deux étapes : la formation de l'acide benzoïque et la cristallisation de celui-ci. Les facteurs cinétiques qui permettent d'accélérer la réaction sont une température élevée et une concentration élevée. Le chauffage à reflux permet de chauffer la réaction sans perdre de matière, en utilisant un système de condensation des vapeurs. L'exercice comporte également des questions sur la quantité de matière d'alcool benzoïque contenue dans un échantillon, ainsi que sur la quantité théorique d'acide benzoïque qui pourrait être obtenue si la réaction était totale. Le rendement de la synthèse est calculé en comparant la masse théorique maximale avec la masse réelle obtenue, donnant un résultat de 61%. Il est souligné que le rendement dépend de la nature de la réaction.
Corrigés de BAC
Bac Physique-Chimie
MPSI/PCSI

Qualité des eaux souterraines (1)
Bonjour à tous, dans cet exercice de chimie des solutions extrait du bac de 2022 de Nouvelle-Calédonie, on aborde le sujet de la contamination de l'eau douce par l'eau salée des littorales. On nous explique que l'eau de mer salée peut pénétrer les nappes phréatiques lors du pompage, ce qui peut contaminer l'eau douce en la rendant saline. La potabilité de l'eau douce est alors compromise en fonction de la concentration en ions chlorure. Une concentration inférieure à 150 mg/L correspond à une absence de contamination, une concentration entre 50 et 200 mg/L est due à une contamination naturelle mais l'eau reste potable, et une concentration supérieure à 200 mg/L rend l'eau impropre à la consommation.
Dans la première question, on nous demande la valeur de la concentration minimale en ions chlorure à partir de laquelle on considère qu'il y a eu intrusion et contamination de l'eau. Cette valeur est de 200 mg/L.
Dans la deuxième question, on doit déterminer la concentration en quantité de matière des ions chlorure apportée par le MgCl2. On sait que le MgCl2 se dissout complètement dans l'eau et que la réaction est totale. On utilise donc un tableau d'avancement pour calculer la concentration en ions chlorure. On obtient une valeur de 8,0 x 10^-2 mol/L.
Enfin, dans la troisième question, on nous donne la concentration massique en ions chlorure apportée par le NaCl et on doit déterminer la concentration totale en ions chlorure dans la mer Méditerranée. On utilise la relation entre la concentration molaire et la concentration massique pour trouver la concentration massique des ions chlorure apportée par le MgCl2, qui est de 2,8 g/L. En additionnant cette valeur à la concentration massique apportée par le NaCl (16,5 g/L), on obtient une concentration totale massique de 19,3 g/L pour les ions chlorure dans la mer Méditerranée.
Dans la vidéo suivante, nous aborderons les parties B et C de cet exercice. N'hésitez pas à poser vos questions en commentaire.
Corrigés de BAC
Bac Physique-Chimie
MPSI/PCSI
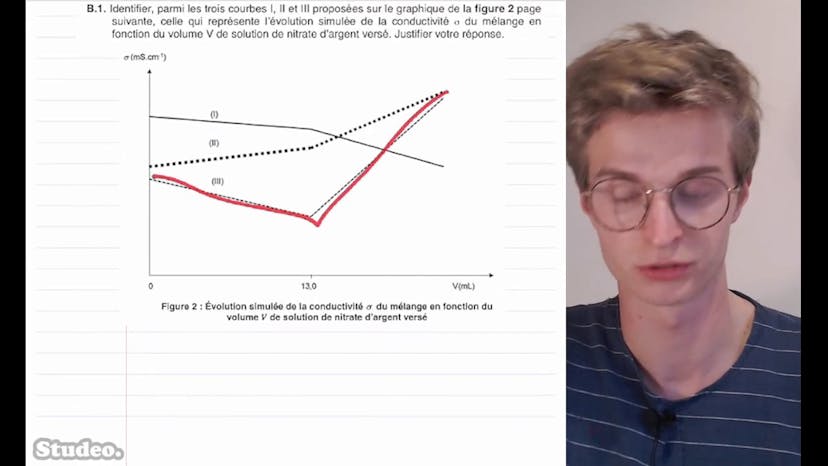
Qualité des eaux souterraines (2)
Dans cette vidéo, on aborde le sujet du titrage des ions chlorures dans les eaux souterraines afin de vérifier leur concentration en masse. On explique d'abord le risque de contamination des nappes phréatiques par les ions chlorures provenant de la mer. Ensuite, on présente l'expérience de titrage qui consiste à prélever 50 mL d'eau douce et à les titrer avec une solution de nitrate d'argent. On suit ce titrage par conductimétrie et on nous demande d'identifier la courbe correspondant à l'évolution de la conductivité en fonction du volume de solution versé. On explique ensuite la réaction de titrage et comment les ions évoluent avant, pendant et après l'équivalence. On constate que la conductivité diminue avant l'équivalence et augmente après. La courbe qui descend puis remonte est donc la bonne. On détermine ensuite que le volume versé à l'équivalence est de 13 mL. Enfin, on calcule la concentration massique en ions chlorures dans l'eau prélevée en utilisant la formule de quantité de matière. On conclut que la concentration est inférieure à la limite de potabilité de 200 mg/L et que l'eau peut être utilisée pour la consommation. Enfin, on aborde la modélisation du titrage via un langage de programmation Python et on identifie les espèces chimiques présentes et leur évolution au cours du titrage. On complète également une ligne de code Python pour calculer la concentration en ions chlorures.
Corrigés de BAC
Bac Physique-Chimie
MPSI/PCSI
Pile à méthanol (1)
Aucun résumé n'est disponible pour cette vidéo
Corrigés de BAC
Bac Physique-Chimie
MPSI/PCSI

Pile à méthanol (1)
Aucun résumé n'est disponible pour cette vidéo
Corrigés de BAC
Bac Physique-Chimie
MPSI/PCSI

Pile à méthanol (2)
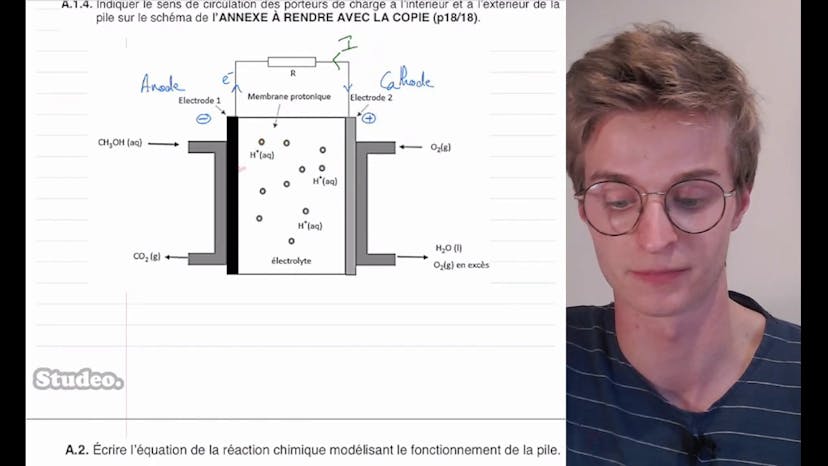
Bonjour à tous, dans cette vidéo, nous allons résoudre un problème concernant la pile au méthanol. Nous commençons en rappelant le fonctionnement de cette pile, puis nous explorons comment des élèves souhaitent utiliser deux piles en série pour faire fonctionner un petit ventilateur. L'intensité du courant mesurée est de 450 mA et chaque pile a un rendement de 70%.
La première question consiste à calculer la capacité électrique théorique de la pile au méthanol étudiée précédemment. La capacité électrique théorique est définie comme le nombre de moles échangées pendant la réaction multiplié par la constante de Faraday (9,65 x 10,4 coulombs par mole). En observant le réactif limitant CH3OH, nous pouvons conclure que 6 moles d'électrons sont impliquées dans la réaction pour une mole de CH3OH. Ainsi, la capacité électrique théorique est égale à 6 fois la quantité de matière en CH3OH multipliée par la constante de Faraday. En effectuant les calculs, nous obtenons une capacité électrique théorique de 16,9 x 10^3 coulombs.
Ensuite, nous abordons la question ouverte: les élèves pourront-ils faire fonctionner leur ventilateur pendant au moins une heure ? Pour répondre à cette question, nous devons calculer la capacité électrique réelle de la pile, en utilisant le rendement de 70%. Comme nous avons deux piles en série, les capacités électriques se cumulent. Ainsi, la capacité électrique réelle est égale à deux fois la capacité électrique réelle de la pile A. En utilisant cette capacité électrique réelle et l'intensité du courant (450 mA), nous pouvons trouver le temps de fonctionnement de la pile en secondes. En effectuant les calculs, nous obtenons un temps de fonctionnement de 5,9 heures, ce qui signifie que les élèves pourront faire fonctionner leur ventilateur pendant largement plus d'une heure.
Si vous avez des questions, n'hésitez pas à les poser en commentaire. À bientôt pour une prochaine vidéo.


