Cours d'apprentissage en ligne

Eclipse solaire du 10 juin 2021 (1)

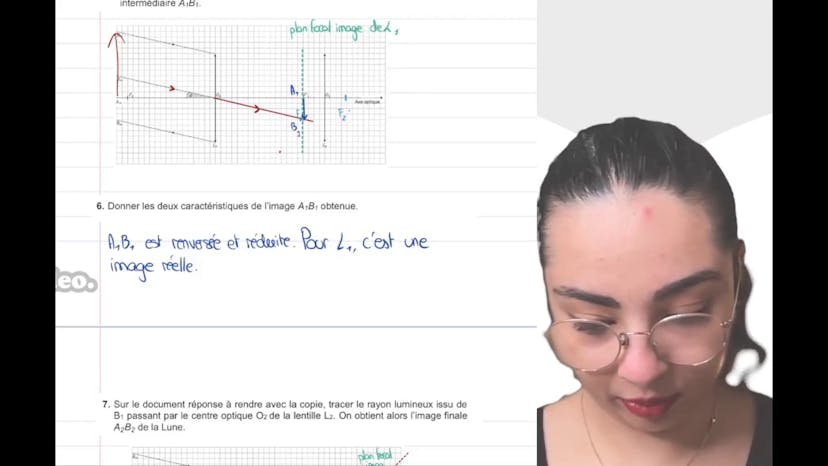
Aujourd'hui, nous allons corriger un exercice sur l'éclipse solaire qui est tombé au Bac l'année dernière en Polynésie. Cet exercice fait partie des exercices optionnels au Bac de Physique. Il porte sur l'optique géométrique et plus précisément sur la lunette astronomique. La lunette astronomique est un instrument à focale composé de deux lentilles convergentes, l'objectif et l'oculaire. Dans la première question, il est demandé d'identifier ces deux termes, ce qui est assez simple à faire. Ensuite, il est demandé de donner le nom scientifique du point où les rayons se croisent pour la lentille L1, il s'agit du foyer principal image. Le texte parle ensuite de l'éclipse du 10 juin 2021 et donne des informations techniques sur la construction de la lunette. On nous demande ensuite de réaliser des constructions. Tout d'abord, on nous demande de positionner le foyer principal objet et le foyer principal image pour une lunette commerciale afocale. Pour cela, il faut que ces deux foyers coïncident, ce qui signifie que les rayons qui les traversent convergent en un point précis. Ensuite, on nous demande de tracer le rayon lumineux issu d'un point B infini passant par le centre optique O1 de la lentille L1. Ce rayon n'est pas dévié et permet d'obtenir l'image intermédiaire B'1. Ensuite, on nous demande de donner les caractéristiques de cette image, qui est réelle, renversée et réduite. Ensuite, on nous demande de tracer le rayon lumineux issu de B'1 passant par le centre optique O2 de la lentille L2 pour obtenir l'image finale, A2, B2 de la lune. Enfin, on nous demande de représenter le faisceau de rayons lumineux issus de B infini passant par les bords des lentilles L1 et L2. Pour cela, il faut tracer les rayons qui se croisent en un point précis et ressortent parallèles, en prenant en compte le point de convergence B. Voilà, c'était un résumé de l'exercice sur l'éclipse solaire et la lunette astronomique.

Eclipse solaire du 10 juin 2021 (2)

Dans cette vidéo, Laila termine l'exercice B sur la lunette astronomique du sujet Polynésie 2022, jour 1. Elle explique qu'il s'agit de questions plus théoriques pour déterminer le grossissement de la lunette. Elle demande aux élèves de positionner l'angle theta prime où est observée l'image finale de la Lune à travers la lunette. Le grossissement de la lunette est défini comme étant theta prime sur theta, avec les angles theta et theta prime étant petits. On peut donc faire l'approximation que tan theta est à peu près égal à theta et tan theta prime est à peu près égal à theta prime. En utilisant la géométrie des triangles formés par les rayons, elle montre comment exprimer le grossissement comme étant égal à A1, B1 fois F1 prime sur F2 prime. Elle propose ensuite aux élèves de calculer la valeur du grossissement pour la lunette utilisée en utilisant les valeurs des focales de l'objectif et de l'oculaire données dans l'énoncé. Le grossissement obtenu est de 73, ce qui est cohérent avec la valeur maximale proposée par le fabricant. Ensuite, Laila aborde le contexte général de l'utilisation de la lunette, notamment en ce qui concerne l'éclipse. Elle explique que la Lune a un diamètre 400 fois plus petit que celui du Soleil, mais elle est aussi 400 fois plus proche de la Terre, ce qui permet un recouvrement presque parfait lors d'une éclipse. Laila donne des directives aux élèves pour déterminer le diamètre de la Lune. Elle suggère de commencer par dessiner un schéma et d'utiliser la trigonométrie pour obtenir une expression reliant le diamètre de la Lune (petit d) au diamètre du Soleil (D) et à l'angle alpha. En utilisant cette relation, elle obtient un diamètre de la Lune de 3,56 fois 10 puissance 3 km. L'article mentionne que le diamètre de la Lune est 400 fois plus petit que celui du Soleil, ce qui correspond à une valeur de 3,48 fois 10 puissance 3 km. L'écart entre les deux valeurs peut être dû à des approximations faites dans l'article. Laila conclut en encourageant les élèves à poser leurs questions dans les commentaires et annonce qu'elle reviendra dans une prochaine vidéo pour l'exercice C.

Acoustique d’une salle (1)

Dans cette vidéo, Leïla du Studio aborde l'exercice C du sujet Polynésie 2022 jour 1 sur l'acoustique d'une salle. Elle commence par expliquer qu'il s'agit d'un exercice de diffraction, d'abord pour les ondes lumineuses puis pour les ondes sonores dans le contexte de l'acoustique d'une salle. Dans la première partie, l'exercice présente une expérience sur la diffraction des ondes lumineuses. Un laser de longueur d'onde inconnue est dirigé vers une fente de largeur irréglable, et un écran est placé à une certaine distance. Le montage expérimental est similaire à celui qui est étudié dans les cours. L'angle caractéristique de la diffraction est donné par θ = λ/a, où θ est en radian, λ est la longueur d'onde, et a est la largeur de la fente. En utilisant l'approximation des petits angles, on peut simplifier cette expression en θ ≈ λ/a. En utilisant de la géométrie, on peut montrer que la largeur L de la tâche de diffraction est donnée par L = 2λd/a. En faisant varier la taille a de la fente, on mesure la largeur L de la tâche centrale et obtient une relation linéaire entre L et 1/a, c'est-à-dire L = k(1/a). On nous demande alors de montrer que cette relation linéaire est justifiée. Leïla explique qu'il y a plusieurs façons de le faire, mais ici elle a choisi de placer les points sur un graphique représentant L en fonction de 1/a, et montre que la courbe est bien une droite passant par l'origine. Il est important de préciser que la droite passe par l'origine pour éliminer toute possibilité d'une ordonnée à l'origine arbitraire. En utilisant la relation L = k(1/a) donnée dans la question précédente, on peut exprimer k en fonction de λ et 2d. Ensuite, l'exercice demande de montrer que la longueur d'onde λ est égale à 6,5 x 10^-7 mètres. Pour cela, il faut interpréter le graphique et utiliser l'expression de k obtenue précédemment. Leïla explique qu'il s'agit de trouver le coefficient directeur de la droite représentée par le graphique, c'est-à-dire la pente de la droite. Elle utilise la formule k = Δy/Δx où Δy est la variation en hauteur et Δx est la variation en longueur. En prenant les points appropriés sur le graphique, elle obtient une valeur pour k, qui permet ensuite de calculer la valeur de λ recherchée. Enfin, l'exercice demande de déterminer la valeur de l'angle θ2 correspondant à une autre fente de longueur a2 = 150 micromètres, sachant que l'angle θ1 correspondant à la fin de la largeur a1 = 38 micromètres est égal à 1,7 x 10^-2 radians. On utilise la même formule que précédemment, c'est-à-dire θ2 = λ/a2, où λ est connu. On calcule θ2 et on constate que θ1 > θ2, ce qui signifie que la diffraction est plus marquée pour la fente de longueur a1. En conclusion, Leïla espère que cette vidéo a été utile et donne rendez-vous pour la suite de l'exercice sur la diffraction sonore.

Acoustique d’une salle (2)

La diffraction des ondes lumineuses a été traitée en première partie de l'exercice. Ensuite, il s'agit d'étudier l'analogie avec les ondes sonores et l'acoustique d'une salle de concert. On nous donne les fréquences f1 = 200 Hz (sons graves) et f2 = 1 kHz (sons aigus) que l'élève perçoit mieux. On doit exprimer la longueur d'onde lambda en fonction de la vitesse du son Vson et de la fréquence f. On obtient lambda = Vson / f. En utilisant cette formule, on détermine les longueurs d'onde lambda1 = 1,70 m et lambda2 = 0,340 m correspondant aux fréquences f1 et f2. Ensuite, on doit choisir parmi les positions A, B et C celle qui correspond le mieux à la situation décrite par l'élève lors du concert. L'élève perçoit mieux les graves que les aigus, donc il faut trouver une position où les graves passent et pas les aigus. On utilise le concept de diffraction, en sachant que la diffraction est plus importante lorsque la largeur de l'obstacle (ici, un pilier) est proche de la longueur d'onde. Comme la fréquence f1 a une plus grande longueur d'onde que f2 et que la largeur du pilier est du même ordre de grandeur que la longueur d'onde, les graves seront plus diffractés que les aigus. En position A, il n'y a pas de diffraction, donc on reçoit les graves et les aigus. En position B, quelle que soit l'angle de diffraction, on est dans une zone où l'on reçoit le son, comme pour la lumière dans une tâche de diffraction lumineuse. En position C, les graves sont plus diffractés, ce qui pourrait expliquer pourquoi l'élève perçoit mieux les graves que les aigus. Donc la position C correspond le mieux à la situation décrite par l'élève. Il est important de bien manipuler les connaissances sur les ondes lumineuses et de faire une analogie avec les ondes sonores pour résoudre cet exercice. Cet exercice permet de s'entraîner et de réviser pour le bac de physique.

Le sel d’oseille (1)

Dans ce cours, Layla de Studéo présente le premier exercice d'un sujet de BAC de chimie sur le sel d'osaïe. Elle commence par expliquer que le sel d'osaïe est en réalité l'acide oxalique, une substance chimique utilisée dans de nombreuses synthèses. L'objectif de l'exercice est de déterminer si l'acide oxalique est un acide fort ou un acide faible. Layla explique ensuite la définition d'une espèce acide selon Brønsted, qui libère un proton H+, et d'une base de Brønsted, qui capte un proton H+. Elle mentionne également les acides de Lewis, liés au doublé électronique. Elle poursuit en montrant la représentation de Lewis de l'acide oxalique et en expliquant pourquoi il est considéré comme un diacide, capable de libérer deux protons H+. Elle donne également les deux couples acides-bases associés à l'acide oxalique. Dans la partie expérimentale, Layla modélise la transformation chimique entre l'acide oxalique et l'eau en supposant que c'est un diacide fort. Elle écrit l'équation de la réaction et utilise un tableau d'avancement pour déduire la concentration en H3O+. Elle trouve une concentration de 1*10^-1 mol par litre. En comparant le pH théorique calculé à partir de la concentration en H3O+ avec le pH expérimental, Layla conclut que l'hypothèse selon laquelle l'acide oxalique est un acide fort n'est pas valide. En effet, la solution est moins acide que prévu, ce qui indique une réaction incomplète et donc, que l'acide oxalique est un acide faible. Layla annonce ensuite qu'elle étudiera cette autre hypothèse dans une prochaine vidéo. Résumé : Layla de Studéo présente le premier exercice d'un sujet de BAC de chimie sur l'acide oxalique. Elle explique les concepts de base et utilise un tableau d'avancement pour déterminer si l'acide oxalique est un acide fort ou faible. Elle conclut que c'est un acide faible.

Le sel d’oseille (2)

Dans cette vidéo, nous terminons le sujet sur les diacides qui est tombé l'année dernière en Polynésie dans l'exercice sur les sels d'ozaïque. Dans la vidéo précédente, nous avons étudié l'acide oxalique et avons invalidé l'hypothèse selon laquelle il s'agirait d'un diacide fort. Nous formulons donc une nouvelle hypothèse selon laquelle l'acide oxalique est en réalité un monoacide faible en solution. Nous donnons les concentrations d'acide apporté et son pKa, ainsi que la réaction associée. Nous remarquons que cette réaction présente des doubles flèches, ce qui indique qu'il s'agit d'une dissociation partielle en équilibre. Nous rappelons que le pH de la solution réalisée est de 1,47, ce qui servira de preuve pour valider ou invalider notre hypothèse. Nous devons également écrire l'équation modélisée de la transformation chimique de l'espèce AH- avec l'eau. Cette réaction est classique et produit un proton et une forme hydratée (H3O+). 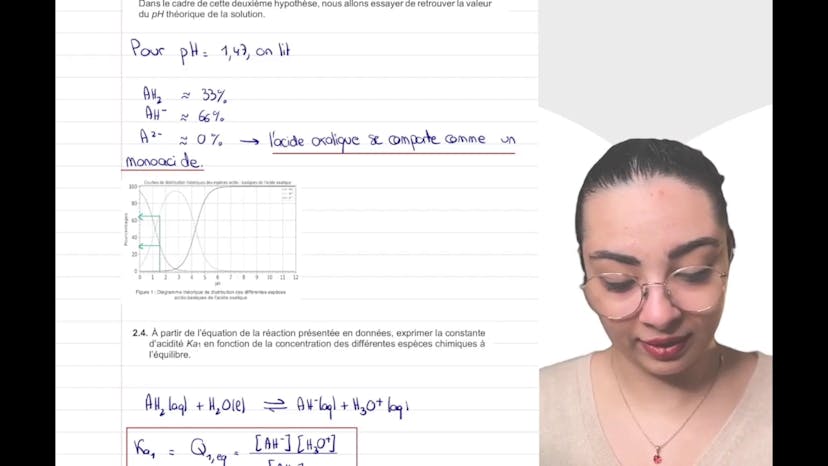En utilisant la figure 1, nous déterminons le pKa de la deuxième acidité de l'acide oxalique. En nous plaçant au point d'intersection de la courbe de distribution théorique, nous trouvons un pH égal à environ 4,3, ce qui correspond au pKa recherché. En utilisant la figure du pH réel, nous donnons une estimation approximative du pourcentage de chaque espèce présente dans la solution. Nous constatons que la concentration de A2- est négligeable et pouvons donc considérer que l'acide oxalique se comporte comme un monoacide. Nous exprimons ensuite la constante d'acidité K1 en fonction des concentrations des espèces à l'équilibre. Nous utilisons le quotient réactionnel de la réaction et l'activité de l'eau pour cela. Nous devons également justifier la concentration en oxonium notée H et vérifier une équation du second degré donnée. En utilisant un tableau d'avancement, nous exprimons les concentrations de chaque espèce en fonction de H et utilisons la constante de réaction KA1 pour établir l'équation du second degré. Enfin, nous utilisons un code Python pour calculer la valeur de KA1 et constatons que le pH final calculé est très proche du pH expérimental, ce qui confirme notre hypothèse selon laquelle l'acide oxalique se comporte comme un monoacide faible. En conclusion, cette vidéo nous a permis de terminer notre étude sur les diacides et de valider l'hypothèse selon laquelle l'acide oxalique se comporte comme un monoacide faible.

Le sel d’oseille (3)

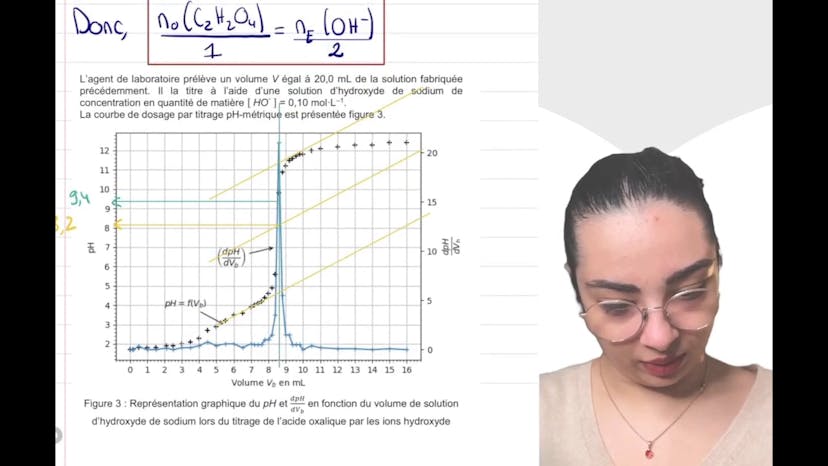
Ce cours concerne l'étude de l'acide oxalique et de ses réactions. On cherche à déterminer si un solide est de forme pure ou hydratée grâce à un titrage par suivi pH métrique. On calcule d'abord la concentration massique avec ses incertitudes. Ensuite, on justifie le coefficient 2 devant l'ion hydroxyde dans l'équation de réaction, en se basant sur le fait que l'acide oxalique est un diacide. On explique également les conditions nécessaires pour utiliser un titrage direct. On donne ensuite la relation entre les quantités de matière en espèce titrée et titrante à l'équivalence. On détermine le pH à l'équivalence en utilisant soit la dérivée de la courbe pH-volume, soit la méthode des tangentes. On choisit un indicateur coloré qui couvre les deux sauts de pH. En utilisant le résultat du titrage, on calcule la concentration en quantité de matière en acide oxalique et on détermine s'il est hydraté ou non. On compare les concentrations massiques et on conclut que l'acide oxalique est hydraté. Le lien entre les concentrations massiques et la détermination de l'hydratation a été réalisé grâce à l'aspect prise d'initiative. Ce cours peut être complété par d'autres vidéos traitant des exercices de physique A, B et C.

Un capteur capacitif

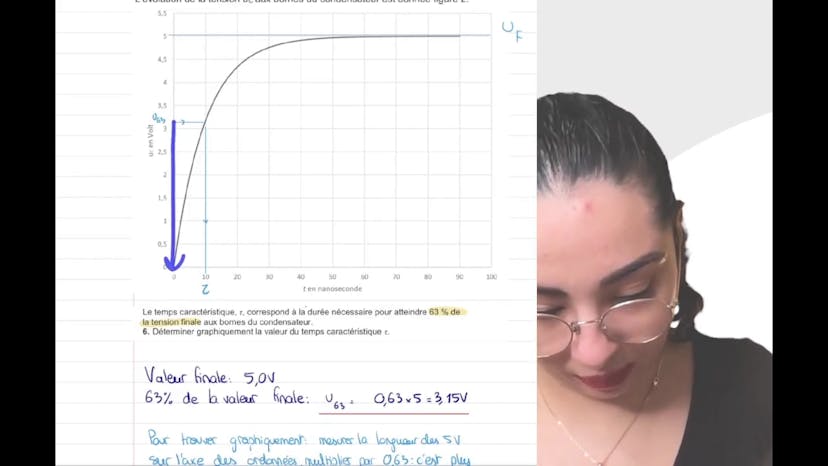
Le cours est une transcription d'une vidéo qui explique un exercice d'électricité sur le capteur capacitif. Le but de l'exercice est d'étudier un dipôle RC en établissant une équation différentielle et en conduisant une étude théorique et expérimentale de la charge. Les principales formules utilisées sont la loi des mailles, la loi d'Ohm et la relation entre le courant d'intensité, la tension aux bornes du condensateur et la capacité du condensateur. Ensuite, la vidéo explique comment déterminer graphiquement la durée nécessaire pour atteindre 63% de la tension finale aux bornes du condensateur et comment calculer la valeur de la capacité C du condensateur. Elle aborde également l'utilisation d'un condensateur à capacité variable et explique comment cela peut être utilisé pour contrôler l'épaisseur d'une colle.

La planète mercure

Aujourd'hui, nous allons aborder l'exercice B du sujet Polynésie de 1022 jour 2, qui porte sur la planète Mercure et notamment sur les concepts de force centrale, études de trajectoire, loi de Kepler, loi de Newton, gravitation, etc. On nous présente tout d'abord des informations sur la planète Mercure, qui est mal connue et proche du Soleil. Sa distance au Soleil varie entre 0.31 et 0.47 UA, et sa vitesse orbitale est de 47 km par seconde. En utilisant un schéma d'une ellipse, on montre que le demi-grand axe de l'orbite de Mercure vaut 0,39 UA. Nous énonçons ensuite la deuxième loi de Kepler, appelée loi des aires, qui stipule qu'une planète balaie des aires égales pendant des durées égales, et nous l'appliquons pour déterminer à quel endroit de sa trajectoire Venus atteint la vitesse de 39 km par seconde. Par la suite, en utilisant les données pertinentes et la troisième loi de Kepler, nous expliquons que Mercure parcourt l'ensemble de son orbite en un peu moins de trois mois. Nous passons ensuite à l'étude de la trajectoire de la sonde Messenger, qui a une période de révolution de 8 heures et une altitude de 200 km. En utilisant les lois de la gravitation et le principe fondamental de la dynamique, nous montrons que l'accélération mesurée à cette altitude permet d'attribuer à Mercure une masse de 3,29 × 10^23 kg. Enfin, nous appliquons la troisième loi de Kepler à la sonde Messenger pour calculer la valeur du demi-grand axe de son orbite, et nous expliquons pourquoi sa trajectoire ne peut pas être considérée comme circulaire. En résumé, cet exercice couvre les concepts de la planète Mercure, des lois de Kepler, de la gravitation et du principe fondamental de la dynamique.

Nos oreilles, on y tient !

Dans ce cours, Layla explique un exercice d'acoustique qui porte sur l'audition et le niveau sonore. Elle utilise des formules qui portent sur les décibels pour déterminer si certaines activités peuvent être nocives pour l'audition. Elle décrit la situation où deux conducteurs sont séparés par une distance et où un autoradio est allumé dans la première voiture. Les fenêtres des deux voitures sont baissées. Layla utilise la formule d'atténuation géométrique pour calculer l'intensité sonore reçue par le conducteur 1 et le conducteur 2. Elle détermine ensuite que l'atténuation géométrique est égale à 9,8 décibels. Layla mesure ensuite le niveau d'intensité sonore avec un sonomètre et trouve un niveau inférieur à celui théorique, ce qui est cohérent. Elle calcule ensuite l'incertitude type de cette atténuation et trouve que l'atténuation est compatible avec les mesures expérimentales. Ensuite, Layla étudie ce qui se passe lorsque les fenêtres sont fermées et explique que cela entraîne une atténuation par absorption. Elle utilise cette information pour déterminer si le conducteur 1 est exposé à un niveau d'intensité sonore supérieur à la limite de nocivité. Elle conclut en disant que le conducteur 1 est effectivement exposé à un niveau sonore supérieur à la limite de nocivité. Le cours est donc centré sur l'atténuation sonore et l'impact sur la santé auditive.

Le colorant E127 (1)

Aujourd'hui, nous allons étudier le colorant E127 utilisé dans certains aliments et médicaments. Ce colorant est ionique et a une forme complexe. Nous allons d'abord étudier les différentes familles fonctionnelles présentes dans sa formule topologique. Ensuite, nous allons analyser les différentes formes du colorant en fonction du pH. Nous allons également doser ce colorant dans un révélateur de plaques dentaires pour déterminer sa concentration. Pour cela, nous utilisons la loi de Beer-Lambert et exploitons les données expérimentales. Nous justifions également la couleur rouge du révélateur en fonction de son spectre d'absorption. Enfin, nous calculons la concentration molaire et le titre massique du colorant dans le révélateur. La concentration molaire est de 2,2 x 10-2 mol/L et le titre massique est de 1,9%. Ces résultats correspondent aux informations données dans l'énoncé.