Cours d'apprentissage en ligne

Le colorant E127 (3)

Le cours porte sur la décoloration du colorant E127 en utilisant de l'eau de Javel. Deux expériences sont réalisées, l'une avec de l'eau de Javel diluée et l'autre avec de l'eau de Javel pure. On étudie l'évolution de la concentration du colorant au cours du temps. Dans la première partie, on décrit qualitativement l'évolution de la vitesse volumique de disparition du colorant. On explique que la vitesse est représentée par la pente de la courbe de concentration en fonction du temps, et que cette pente est négative car la concentration diminue. Ensuite, on propose un facteur cinétique qui peut expliquer la diminution de la vitesse au cours du temps, qui est la diminution de la concentration en réactif. On mentionne que ce facteur cinétique peut être une bonne explication même si on n'est pas sûr à cent pourcent. Dans la deuxième partie, on détermine graphiquement le temps de demi-réaction pour l'expérience A, en cherchant le temps nécessaire pour atteindre la moitié de la concentration initiale. On trouve que cela prend environ 150 secondes. On explique que le temps de demi-réaction permet d'estimer quand la réaction est terminée, et qu'au bout de 5 fois le temps de demi-réaction, la réaction est complète. Enfin, on discute de l'optimisation de la décoloration du filtre Buchner. On explique que l'objectif est d'augmenter la vitesse de réaction. En comparant les deux expériences, on remarque que l'expérience avec de l'eau de Javel pure est presque deux fois plus rapide que l'expérience avec de l'eau de Javel diluée. On conclut donc que pour optimiser la décoloration, il est préférable d'utiliser de l'eau de Javel pure. En résumé, le cours concerne la décoloration du colorant E127 avec de l'eau de Javel. On analyse l'évolution de la concentration du colorant au cours du temps, on propose des explications pour la diminution de la vitesse de disparition du colorant, on détermine graphiquement le temps de demi-réaction et enfin on discute de l'optimisation de la décoloration en utilisant de l'eau de Javel pure.

La physique du jonglage

Aucun résumé n'est disponible pour cette vidéo

Refroidissement d’un fer à cheval

Le cours porte sur le refroidissement d'un fer à cheval. Il comprend deux parties : le chauffage du fer et le refroidissement du fer. Dans la première partie, on détermine la masse du fer à cheval en utilisant la masse volumique du fer. Ensuite, on calcule la variation d'énergie interne du fer lors du chauffage. On interprète cette variation comme une augmentation de l'énergie cinétique microscopique des atomes de fer. Dans la deuxième partie, on étudie le refroidissement du fer à l'air libre et dans l'eau. On utilise le premier principe de la thermodynamique pour obtenir une équation différentielle qui régit l'évolution de la température lors des pertes thermiques. On vérifie si une fonction proposée est solution de cette équation. On calcule ensuite la valeur de la température du fer lorsqu'il est posé sur la face intérieure. Enfin, on analyse les résultats et on propose des raisons pour lesquelles le modèle utilisé pour le refroidissement dans l'eau ne semble pas cohérent, en citant notamment les pertes de chaleur par rayonnement et les variations de température de l'eau.

Défibrilateur cardiaque

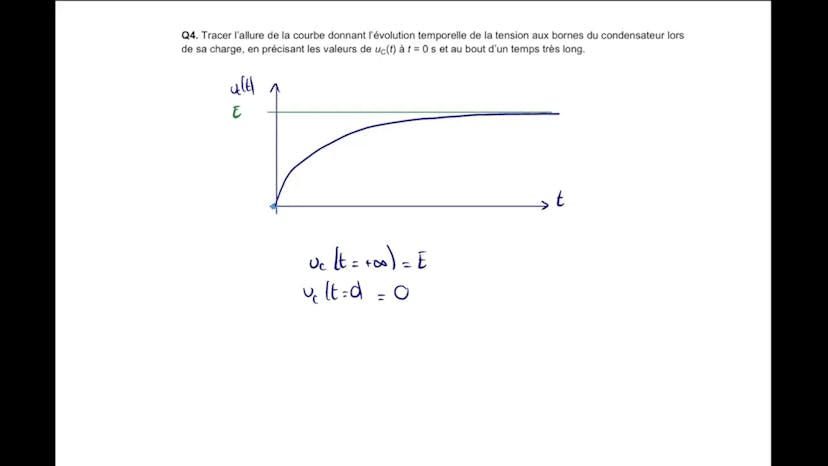
Le sujet de cet exercice C porte sur l'étude d'un défibrillateur cardiaque, qui est un circuit RC. Dans un premier temps, il est demandé de déterminer dans quelle position mettre l'interrupteur pour charger le condensateur. Il faut que l'interrupteur soit en position 1 pour que le générateur et le condensateur soient dans la même boucle. Ensuite, il faut trouver l'équation différentielle du circuit en utilisant la loi des mailles et les lois de fonctionnement de chaque dipôle. En résolvant l'équation, on obtient l'expression recherchée. Il faut ensuite vérifier que la solution est sous la forme demandée. On calcule également le taux de charge du condensateur, qui correspond à la constante de temps du circuit. Il est également demandé de tracer la courbe de l'évolution temporelle de la tension. On montre que le condensateur atteint 99% de sa valeur finale au bout de 5 taux de charge. Ensuite, on s'intéresse à la décharge du condensateur. On détermine graphiquement l'instant où l'interrupteur bascule de la position 1 à la position 2. On trace également la tangente à l'origine pour déterminer le temps caractéristique de décharge. On estime ensuite la durée nécessaire de décharge du condensateur en fonction de la résistance du corps humain. On conclut en montrant que la décharge est inférieure aux 4 secondes prévues pour le choc et que le choc dure donc moins d'une seconde.

Observation de la planète Mars (1)

Leïla de Studio présente le premier exercice d'un sujet tombé l'année dernière en métropole portant sur l'observation de la planète Mars. Cet exercice est noté sur 10 points et concerne la physique. Dans cette introduction, Leïla introduit le sujet en expliquant qu'on souhaite évaluer les caractéristiques de Mars. Elle présente également les formules générales et les valeurs numériques qui seront utilisées tout au long de l'exercice. 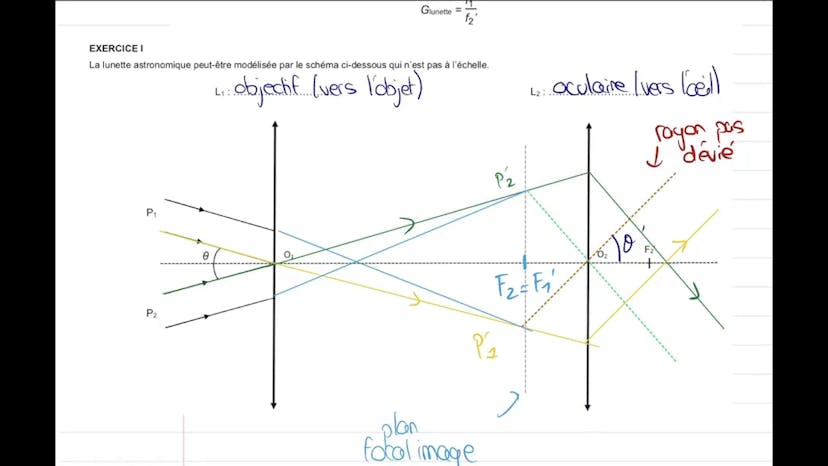Dans la première partie de l'exercice, on s'intéresse à l'observation de Mars avec une lunette astronomique. Leïla explique comment différencier l'objectif de l'oculaire sur le schéma fourni. Elle souligne également que la lunette astronomique est affocale, ce qui signifie qu'elle renvoie une image à l'infini d'un objet situé à l'infini. Cela évite la fatigue des yeux. Pour cela, il faut que F2 soit égal à F1'. Ensuite, il est demandé de tracer les marges des rayons lumineux. Leïla explique qu'il faut tracer des rayons importants, notamment ceux qui passent par le centre des lentilles. Elle montre comment tracer ces rayons et souligne que les autres rayons peuvent suivre le même principe. Le calcul du grossissement de la lunette utilisée est demandé. Leïla montre la formule à utiliser et fait l'application numérique pour trouver un grossissement de 45. Enfin, il est demandé de justifier l'observation d'un observateur qui regarde Mars à l'œil nu et qui voit un point lumineux. Leïla explique que cela s'explique par le fait que l'angle de vision de l'observateur est inférieur à l'angle de résolution de l'œil, ce qui fait que les deux rayons lumineux provenant du sommet et du bas de Mars convergent sur la même cellule de la rétine, donnant l'impression d'un point unique. En utilisant la lunette astronomique, l'observateur voit un disque car le grossissement permet de distinguer les deux points de la planète Mars. Leïla fait le calcul pour trouver l'angle de vision à travers la lunette. En conclusion, Leïla espère que cet exercice aura été utile et annonce la suite du sujet.

Observation de la planète Mars (2)

Dans cet exercice, nous avons étudié la façon de déterminer le diamètre de la planète Mars en utilisant des mesures d'angle effectuées à travers une lunette astronomique. Nous avons commencé par identifier les angles θ1 et θ2 sous lesquels Mars est observée depuis les points A et B. En utilisant la figure 2, nous avons montré que le diamètre de Mars, dm, s'exprime par la formule θA = dm/D. Nous avons également noté que le diamètre de Mars peut être exprimé en fonction de grandes distances, grand D1 et grand D2, qui sont deux fois la distance Soleil-Mars. En effectuant des calculs numériques, nous avons obtenu une valeur de dm égale à 6,8 × 10^3 km, qui est proche du diamètre moyen de référence. Cette méthode s'est donc avérée efficace pour déterminer le diamètre de Mars.

Observation de la planète Mars (3)

Dans cette vidéo, nous terminons l'exercice 1 du sujet de bac qui porte sur l'observation de la planète Mars. Les deux premières parties de cet exercice ont porté sur l'étude de Mars du point de vue optique. Nous avons utilisé la lunette astronomique pour déduire le diamètre de Mars. Dans cette dernière partie, nous nous intéressons à la masse de Mars en utilisant les lois de Newton. Nous assimilons Mars à une sphère de diamètre dm et de masse M, environ dix fois plus petite que celle de la Terre. Pour déterminer cette masse, nous observons le satellite naturel de Mars, Phobos, et utilisons les lois de Newton. Nous connaissons la période de révolution de Phobos, sa trajectoire et le fait qu'il est soumis uniquement à la force de gravitation de Mars. Pour déterminer la vitesse de Phobos sur son orbite circulaire, nous utilisons la deuxième loi de Newton avec un bilan des forces. Nous utilisons le système Phobos dans le référentiel centré sur la masse de Mars et faisons un bilan des forces. Nous déduisons que la force gravitationnelle est égale à la masse multipliée par l'accélération. Nous utilisons ensuite la formule de l'accélération dans le repère de Freinet pour les mouvements de planètes circulaires, qui nous permet d'exprimer l'accélération en fonction de la vitesse et du rayon de l'orbite. En isolant la vitesse, nous obtenons l'égalité v²/rmp = gm/rmp², où g est la constante de gravitation et mm est la masse de Mars. Pour déterminer la masse de Mars, nous devons prendre des initiatives et présenter notre méthode. Nous connaissons la période de révolution de Phobos et le rayon de son orbite. Nous avons également établi une relation entre la vitesse et la masse de Mars. Nous utilisons la propriété d'une orbite circulaire pour établir le lien entre la vitesse, la période et le rayon. En égalant les deux expressions de la vitesse obtenues précédemment, nous pouvons isoler la masse de Mars. En résolvant numériquement, nous obtenons une valeur de 464 x 10^23 kg, environ dix fois plus grande que la masse de la Terre, ce qui est cohérent. En conclusion, cet exercice nous a permis d'utiliser les lois de Newton pour déterminer la masse de la planète Mars en observant son satellite Phobos.

Solution désinfectante (1)

Aucun résumé n'est disponible pour cette vidéo

Solution désinfectante (2)

Dans cette vidéo, Matisse du Studio aborde l'exercice de titrage de l'acide lactique dans une solution désinfectante. Avant de commercialiser le produit, un laboratoire réalise un test de qualité en utilisant un titrage acido-basique suivi par conductimétrie après avoir dilué la solution. Le but de l'exercice est de proposer un protocole expérimental pour préparer 100 ml de solution désinfectante diluée 5 fois. Pour cela, il faut utiliser une pipette jaugée, une fiole jaugée et de l'eau distillée. En utilisant le facteur de dilution, on détermine que 20 ml de la solution de base doivent être prélevés. Le protocole consiste ensuite à prélever ces 20 ml de solution à l'aide de la pipette jaugée, à les verser dans la fiole jaugée de 100 ml et à compléter jusqu'au trait de jauge avec de l'eau distillée. Ensuite, dans un bécher de 250 ml, on introduit 20 ml de la solution désinfectante diluée et on ajoute 150 ml d'eau distillée. Le titrage est réalisé en utilisant une solution aqueuse d'hydroxyde de sodium de concentration CB. On doit écrire l'équation de la réaction de titrage, qui est une réaction acide-base où l'acide AH réagit avec l'hydroxyde HO- pour former l'ion A- et de l'eau H2O. On doit également interpréter qualitativement le changement de pente de la courbe de titrage observé à proximité de l'équivalence. On explique que ce changement est dû aux conductivités ioniques molaires des différentes espèces présentes dans le bécher. La concentration de HO- augmente plus rapidement que celle de A-, ce qui entraîne une augmentation plus importante de la conductivité. Enfin, on nous demande de déterminer graphiquement la valeur du volume à l'équivalence et d'évaluer la concentration de la solution en acide lactique avant dilution. En traçant les deux segments de droite sur le graphe, on trouve que le volume à l'équivalence est de 8,6 ml. En utilisant la formule de concentration diluée, on trouve une concentration en acide lactique de 0,22 mol/L, avec une incertitude de 0,03 mol/L. En résumé, cette vidéo présente un exercice de titrage acido-basique suivi par conductimétrie pour déterminer la concentration de l'acide lactique dans une solution désinfectante. Elle explique également comment préparer une solution diluée et interpréter les résultats du titrage.

Observation de la Lune depuis la Terre (1)

Dans cette vidéo, on aborde le sujet de l'observation de la Lune depuis la Terre. On présente les mots-clés importants tels que orbite, période de révolution, lunette astronomique et grossissement. Ensuite, on procède à la correction de l'exercice, en commençant par expliquer les différentes caractéristiques de la Lune que l'on peut observer depuis la Terre. On mentionne également qu'il existe plusieurs millions de cratères, bien que l'on puisse en voir seulement plusieurs dizaines de milliers depuis notre planète. La première partie de l'exercice consiste à comprendre l'expression "la face cachée de la Lune". On se place dans un référentiel géocentrique, où l'origine est le centre de la Terre. On précise les différentes données nécessaires à l'étude, telles que la constante de gravitation, la distance moyenne entre la Terre et la Lune, la base de la Terre, et la vitesse du centre de la Lune sur son orbite. La première question de l'exercice demande d'établir l'expression de la période de révolution de la Lune autour de la Terre, puis de calculer sa valeur. On utilise la vitesse de la Lune et la distance terrestre pour déterminer cette période. On obtient finalement une valeur numérique de 2,37 x 10^6 secondes. La deuxième question consiste à comparer cette période de révolution avec la période de rotation de la Lune sur elle-même. En calculant le rapport entre ces deux valeurs, on trouve une valeur proche de 1. Cela signifie que la Lune met presque autant de temps à faire le tour de la Terre qu'à effectuer une rotation complète sur elle-même. La troisième question demande d'ajouter la position de la Lune et du point P, qui sert à traquer la rotation de la Lune, aux différentes dates indiquées dans le schéma fourni. On justifie également pourquoi on parle de la face cachée de la Lune dans le cadre de ce modèle simplifié. En observant le schéma, on réalise que le point P est toujours diamétralement opposé au point d'observation depuis la Terre. Ainsi, peu importe où l'on se trouve sur Terre, le point P est toujours "caché" et tourné vers l'opposé de nous, d'où l'appellation de "face cachée de la Lune". En conclusion, cet exercice permet d'aborder de manière ludique et intéressante le langage commun et les concepts de l'observation de la Lune. On utilise des outils de bases en physique pour expliquer des concepts puissants. C'est un début d'exercice très plaisant qui présente des questions stimulantes.

Observation de la Lune depuis la Terre (2)

Dans cette vidéo, Mathis parle du cratère Tichot, situé dans l'hémisphère sud de la Lune. Il nous donne des informations sur sa création, ses dimensions, et ses montagnes. Ensuite, il explique l'objectif de la deuxième partie de l'exercice, qui est de concevoir une lunette astronomique permettant d'observer les détails de la surface lunaire depuis la Terre. Il donne des données sur la distance Terre-Lune et le pouvoir séparateur de l'œil humain. Il utilise ces informations pour calculer l'angle sous lequel le cratère Tichot est vu depuis la Terre et détermine qu'il est impossible de distinguer ses contours à l'œil nu. Il explique ensuite comment une lunette astronomique fonctionne, et comment les lentilles jouent le rôle de l'objectif et de l'oculaire. Il décrit ensuite la marche du faisceau lumineux à travers la lunette et comment l'image se forme à l'infini. Il explique que la lunette est qualifiée d'afocale car elle ne nécessite pas d'accommodation de l'œil et situe l'image à l'infini. Il donne la formule du grossissement de la lunette en fonction des angles θ et θ' et explique l'intérêt de construire une lunette astronomique qui grossit les images. Enfin, il aborde un problème de résolution concernant la distance focale de l'oculaire pour pouvoir distinguer les montagnes du cratère Tichot et explique la démarche à suivre pour trouver la valeur limite de cette distance focale. Il conclut en soulignant l'intérêt de cet exercice qui aborde plusieurs points sur la dynamique céleste.