 Tous les sujets
Tous les sujets Maths
Maths Physique-Chimie
Physique-Chimie Corrigés de BAC
Corrigés de BAC Révisions Maths lycée
Révisions Maths lycée Prépa Examens
Prépa Examens
Terminale
Première
Seconde
MPSI/PCSI
2BAC SM Maroc
 Tous les sujets
Tous les sujets Maths
Maths Physique-Chimie
Physique-Chimie Corrigés de BAC
Corrigés de BAC Révisions Maths lycée
Révisions Maths lycée Prépa Examens
Prépa Examens
Révisions Physique Lycée
Chimie
MPSI/PCSI
Craquage du pentane
Aucun résumé n'est disponible pour cette vidéo
Révisions Physique Lycée
Chimie
MPSI/PCSI
Kevlar
Aucun résumé n'est disponible pour cette vidéo
Révisions Physique Lycée
Chimie
MPSI/PCSI
Synthèse des protéines
Aucun résumé n'est disponible pour cette vidéo
Révisions Physique Lycée
Chimie
MPSI/PCSI
Synthèse des protéines bis
Aucun résumé n'est disponible pour cette vidéo
Révisions Physique Lycée
Chimie
MPSI/PCSI
Acide benzoïque
Aucun résumé n'est disponible pour cette vidéo
Révisions Physique Lycée
Chimie
MPSI/PCSI
Analyse de synthèses
Aucun résumé n'est disponible pour cette vidéo
Révisions Physique Lycée
Chimie
MPSI/PCSI
BAC : Chimie verte
Aucun résumé n'est disponible pour cette vidéo
Révisions Physique Lycée
Chimie
MPSI/PCSI
BAC : Cellulose
Aucun résumé n'est disponible pour cette vidéo
Physique-Chimie
Physique
MPSI/PCSI
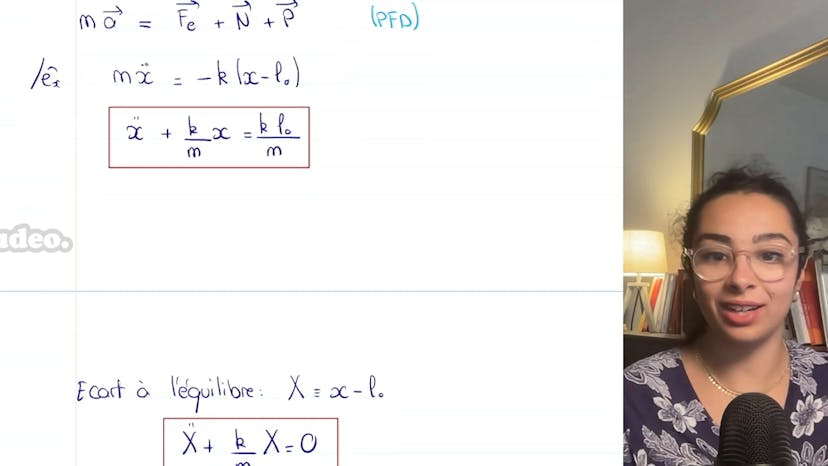
Masse-ressort
Dans cet exercice sur les oscillateurs mécaniques, nous cherchons à déterminer l'équation du mouvement pour un système masse-ressort horizontal.
Tout d'abord, il est conseillé de représenter deux situations différentes : l'équilibre et une légère compression ou extension du ressort. En analysant les forces en présence, nous constatons le poids (P = mg), la réaction du support (N) qui compense le poids mais n'affecte pas le mouvement, et la force de rappel élastique (FE = -KX) où X représente l'extension ou la compression du ressort (dans la direction de l'étirement).
En projetant le principe fondamental de la dynamique sur l'axe de l'extension X, nous obtenons l'équation MX'' = -KX. Pour simplifier, nous posons X' = X - L0, où L0 est la position d'équilibre. Cette équation devient alors homogène : X'' + (K/M)X = 0.
En effectuant un changement de variable et en décalant le repère, nous trouvons l'équation d'oscillateur harmonique : X'' + ω0^2X = 0, avec ω0^2 = K/M. Cette équation est fondamentale en physique et apparaît fréquemment.
Physique-Chimie
Physique
MPSI/PCSI

Oscillateur harmonique
Dans cette vidéo, nous poursuivons notre série en résolvant l'équation différentielle d'un oscillateur harmonique. Nous examinons spécifiquement l'équation d'oscillateur harmonique que nous avons abordée dans la vidéo précédente pour le système de masse ressort, mais qui est également applicable à de nombreux autres types de systèmes.
Dans cette équation, x représente l'écart par rapport à l'équilibre. Pour bien comprendre d'où cela vient, nous adoptons une approche mathématique et vous verrez ensuite qu'il existe des raccourcis en physique. L'équation caractéristique de cette équation différentielle est r² + ω0² = 0, ce qui donne les solutions r = ±iω0. En combinant les exponentielles de chacune de ces solutions, nous obtenons AEiω0t + BE-iω0t.
Cependant, en physique, nous nous intéressons uniquement aux nombres réels. Ainsi, si nous exprimons ces solutions en réel, nous obtenons une forme λcosω0t + μsinω0t. Une autre façon pratique de l'écrire est de prendre x0 au lieu de λ, ce qui nous donne une expression de la forme x0cosω0t. Vous pouvez choisir la méthode qui vous convient le mieux. Personnellement, j'aime les combinaisons linéaires de cosinus et de sinus, car je m'y suis habitué et je trouve que cela fonctionne bien. Cependant, le déphasage peut parfois être plus pratique.
Si nous n'avons pas de vitesse initiale, x.0 = 0 et x(0) = x0. Dans ce cas, la constante λ est égale à x0 et la constante μ est égale à 0. Cela nous donne donc xt = x0cosω0t. Si nous considérons exactement le même type d'expression avec φ = 0, nous pouvons utiliser la même méthode pour les conditions initiales.
Physique-Chimie
Physique
MPSI/PCSI

Pendule simple
Dans ce cours, nous examinons le pendule simple et cherchons à déterminer son équation du mouvement. Le pendule simple se compose d'un fil attaché à une masse, et nous repérons sa position par l'angle theta.
En appliquant le principe fondamental de la dynamique et en faisant un bilan des forces, nous avons le poids orienté vers le bas et la tension du fil qui maintient la bille attachée. En coordonnées polaires, nous utilisons les dérivations des vecteurs de base, ce qui simplifie les calculs.
Nous obtenons les équations suivantes : -ML*theta point carré = P*cos(theta) - T et ML*theta seconde = -P*sin(theta). L'équation qui permet de déterminer la tension du fil est T = P*cos(theta) - ML*theta point carré.
L'équation du mouvement du pendule simple est donnée par theta seconde + (G/L)*sin(theta) = 0. En utilisant l'approximation des petits angles, où sine theta est approximativement égal à theta, nous obtenons l'équation d'un oscillateur harmonique : theta seconde + (G/L)*theta = 0.
La constante propre de cet oscillateur harmonique est la racine carrée de G/L.
J'espère que cela vous a été utile et je vous retrouve bientôt pour la suite.
Physique-Chimie
Physique
MPSI/PCSI
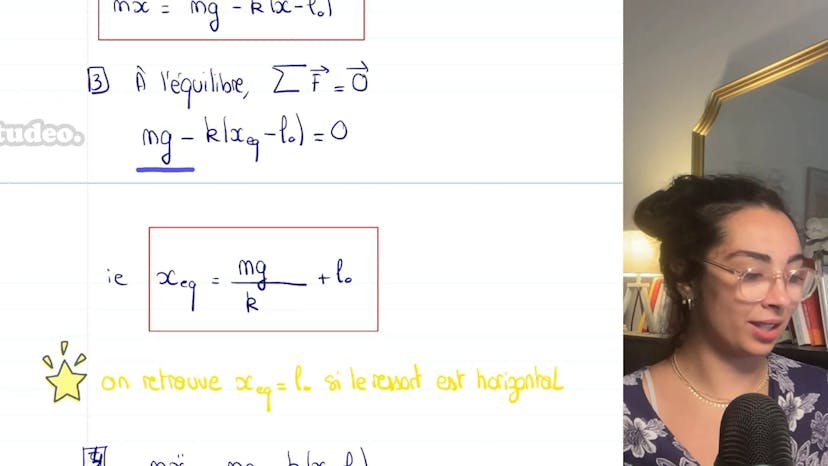
Oscillations non-amorties
Dans cet exercice, nous étudions les oscillateurs harmoniques non amortis. Nous nous intéressons spécifiquement à un système masse-ressort vertical, en négligeant la poussée d'Archimède et les frottements. Tout d'abord, nous faisons un bilan des forces qui agissent sur la masse m. Les forces incluent le poids dirigé vers le bas (mgex) et la force de rappel du ressort (kx-l0ex). Nous vérifions que la force de rappel ramène le ressort vers sa position d'équilibre lorsqu'il est étiré. Ensuite, nous déterminons l'équation différentielle en utilisant le principe fondamental de la dynamique projetée sur ux. Nous obtenons mx² = mgex-kx-l0. Lorsqu'il atteint la position d'équilibre, les forces se compensent, ce qui donne mg-kx-l0 = 0. La position d'équilibre est ainsi donnée par xex = l0 + mg/k. Cette relation montre que plus la masse est grande, plus la position d'équilibre est basse par rapport à l0. L'équation différentielle vérifiée par x en fonction de x, xex, m et k est transformée en une forme plus simple en introduisant l'écart à la position d'équilibre (x - xex). L'équation devient x seconde + ω0²x = 0, avec ω0² = k/m. Nous pouvons alors déterminer la période du mouvement, t0 = 1/(2π√(m/k)). Enfin, nous résolvons l'équation en prenant en compte les conditions initiales où la masse est à l'équilibre (x = 0) mais possède une vitesse v0 dirigée vers le bas (x = v0). La solution générale est donnée par x(t) = v0/ω0 sin(ωt). Cette résolution inclut les étapes classiques pour ce type d'exercice, notamment l'application du principe fondamental de la dynamique, le changement de variable et la résolution de l'équation différentielle.


