Cours d'apprentissage en ligne

test

Aucun résumé n'est disponible pour cette vidéo

Ce cours aborde les exercices de mathématiques qui impliquent des sommes de sinus et de cosinus. En utilisant un cercle trigo, les valeurs des angles sont placées et les valeurs des sinus et cosinus associées peuvent être extraites rapidement. Dans l'un des exemples, les valeurs s'annulent et il ne reste que 0. Pour résoudre certains problèmes, il est important de connaître les valeurs clés de sinus et de cosinus, comme celles pour π sur 6, π sur 4, π sur 3, π sur 2, et 0. Les angles sont également présentés comme demi-racines successives dans l'ordre de leur valeur croissante. En utilisant ces connaissances sur les valeurs clés et le cercle trigo, le cours montre comment résoudre efficacement l'exercice.

Petit problème cercle trigo

Dans cet exercice de trigonométrie, on doit trouver les coordonnées de quatre points d'un carré à partir d'un point donné. Le premier point est donné par ses coordonnées, qui sont liées à la trigo, et se trouve sur le cercle de rayon 1 de centre haut, associé à l'angle pi sur 4. En utilisant la définition géométrique du carré, on peut trouver les coordonnées des autres points en observant que les diagonales se coupent en leur milieu, sont perpendiculaires et ont une même longueur. Pour trouver les coordonnées des points B et D, on ajoute plus pi sur 2 au premier angle, pour obtenir des angles de 3pi sur 4 et 7pi sur 4 respectivement. On peut ensuite lire facilement les coordonnées de ces points sur le cercle trigo en utilisant les valeurs du sinus et du cosinus. En utilisant la caractérisation du carré par ses diagonales, on peut trouver les coordonnées de tous les points du carré.

Exo bilan sur les changements de variable X=...

Dans cet exercice, on utilise une fonction contenant uniquement la variable inconnue X en termes de causes. Pour résoudre l'équation, on utilise un changement de variable en remplaçant X par X² et X. On résout ensuite les racines X1 et X2 et on les compare à la contrainte de l'intervalle de X entre -1 et 1. Ensuite, on résout F2X égale à 0 en utilisant les valeurs de X1 et X2, qui sont ensuite comparées à un deuxième inéquation pour obtenir la réponse finale.

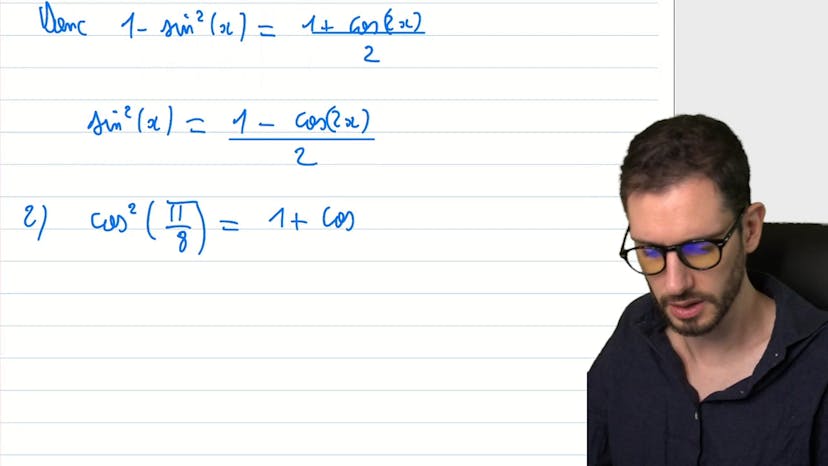
Valeur particulière d'un cos

Ce cours explique comment trouver la valeur de cos ou sin d'un réel donné en utilisant une formule admise. Pour trouver sin²x en fonction de cos²x, on utilise l'identité fondamentale de l'intrigo, sin²x + cos²x = 1. Pour trouver cosinus et sinus de pi sur 8, on utilise la formule cos²x = 1 + cos2x le tout sur 2. Ensuite, il est important de justifier pourquoi la solution positive est la bonne. En effet, pour pi sur 8, le cosinus et le sinus doivent être positifs car l'angle est compris entre 0 et pi sur 2. Enfin, il est recommandé de poser des questions dans le forum si besoin.

Démo inégalité convexité

Le cours explique comment démontrer que le point M est sur la séquente d'une fonction convex F. Pour cela, on utilise les points a et b associés aux réels x et y et un point M défini par des formules. On montre d'abord que l'ordonnée de M est bien sur la séquente en utilisant des calculs et des formules liées aux moyennes pondérées. Ensuite, on montre que M est sur le segment AB en utilisant l'équation d'une droite passant par a et b et en vérifiant que M satisfait cette équation. Enfin, on conclut que l'image de la piscine de M par la séquente est au-dessus de son image par F, ce qui permet de démontrer que M est sur la séquente de F.

Démo au programme : convexité et f''

En résumé, si f est une fonction deux fois dérivable et que f'' est positive sur un intervalle i, alors la courbe représentative de f est au-dessus de ses tangentes sur cet intervalle. La démonstration se fait en posant une fonction phi qui compare la courbe de f et la tangente en un point a, et en montrant que cette fonction est toujours positive ou nulle grâce à l'étude de sa dérivée. Il faut bien comprendre chaque étape de la démonstration et être capable de la reproduire sur une feuille blanche.

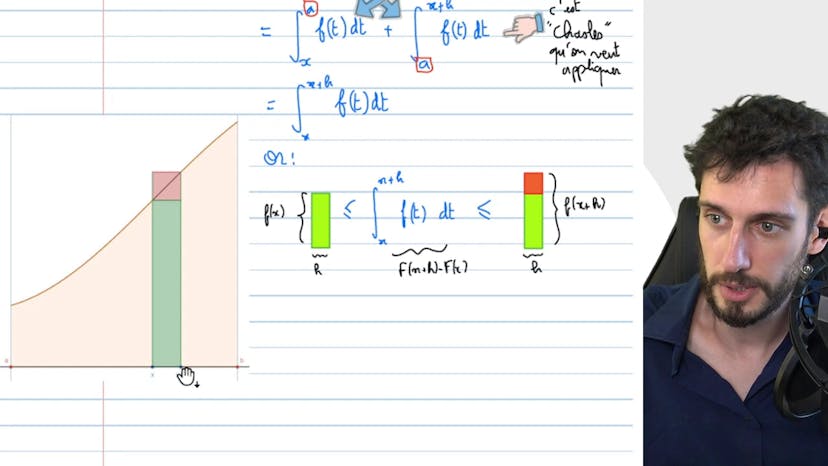
Théorème fondamental : Démo

Dans cette vidéo, l'auteur démontre le théorème fondamental de l'analyse, qui stipule que pour une fonction continue f sur l'intervalle [a, b], la fonction F définie comme l'intégrale de f entre a et x est dérivable, avec pour dérivée f. Il explique également que toute fonction continue sur un intervalle aura des primitifs sur cet intervalle. La démonstration passe par l'utilisation des propriétés des intégrales, de la méthode d'approximation par des rectangles et du théorème d'encadrement. Il est important de comprendre cette démonstration pour l'examen.

Cours par cas pratiques !

Dans ce cours, nous apprenons à déterminer le nombre d'anagrammes pour différents mots. Un anagramme est une combinaison de lettres d'un mot, où l'ordre des lettres importe. Par exemple, pour le mot ABC, les anagrammes possibles sont BAC, CBA, CAB, etc. Pour calculer le nombre d'anagrammes, nous utilisons la notion de permutations. Le nombre d'anagrammes d'un mot est égal au nombre de façons de ranger les lettres du mot. Par exemple, pour le mot ABC, il y a 3! (3 factorielle) possibilités, car il y a 3 lettres et 3 cases pour les ranger. Cependant, lorsque certaines lettres sont répétées, nous devons prendre en compte les permutations de ces lettres. Par exemple, pour le mot AXA, il y a 3! possibilités au départ, mais nous divisons le résultat par 2, car les deux A peuvent être permutés de deux manières différentes. De manière plus générale, pour un mot comme CHIEN, nous calculons d'abord le nombre d'anagrammes sans tenir compte des lettres répétées (5! dans ce cas), puis nous divisons le résultat par le produit des factorielles des nombres de permutations possibles pour chaque lettre répétée. Par exemple, pour le mot ABRACADABRA, il y a 11! possibilités au départ, mais nous devons diviser le résultat par 5! (pour les A), 2! (pour les B) et 2! (pour les R), car ces lettres sont répétées. Cette méthode permet de calculer efficacement le nombre d'anagrammes pour différents mots en prenant en compte les lettres répétées.

Exo type en une minute !

Ce cours porte sur un test composé de quatre questions indépendantes, avec des réponses vrai ou faux. Le candidat répond au hasard, sans connaître les réponses. La question est de déterminer la probabilité pour le candidat d'obtenir les quatre réponses correctes, ou plus précisément, combien de scénarios mèneraient à cette réussite. En utilisant la formule de calcul des puissances, on trouve qu'il y a 16 choix possibles au total. Donc, si vous répondez au hasard, il y a une chance sur 16 d'obtenir les quatre réponses correctes. Cette petite expérience est intéressante et amusante.

Entiers dont la somme des chiffres vaut 3

Le cours se concentre sur la résolution d'un exercice mathématique portant sur les nombres entiers. On cherche à déterminer combien de nombres inférieurs à 10^P existent, où P est un entier naturel. On explique que le nombre de ces nombres est égal à 10^P + 1, car il y a 10^P chiffres possibles, plus le 0. Ensuite, on