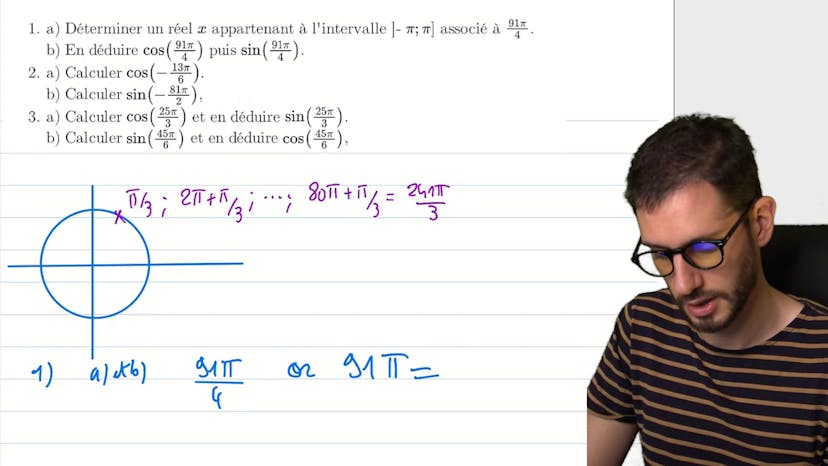Tous les sujets
Tous les sujets Maths
Maths- Nombres et calculs
- Géométrie
- Fonctions
- Stats et Probas
- Analyse
- Suites Numériques
- Second degré
- Dérivation
- Exponentielle
- Trigonométrie
- Géométrie
- Probas et Stats
- Analyse (spé)
- Géométrie (spé)
- Probabilités (spé)
- Arithmétique (exp)
- Complexes (exp)
- Analyse
- Algèbre
- Analyse
- Algèbre
- Probabilités
SecondePremièreTerminale2BAC SM MarocMPSI/PCSI Physique-Chimie
Physique-Chimie Corrigés de BAC
Corrigés de BAC Révisions Maths lycée
Révisions Maths lycée Prépa Examens
Prépa Examens
 Tous les sujets
Tous les sujets Maths
Maths- Nombres et calculs
- Géométrie
- Fonctions
- Stats et Probas
- Analyse
- Suites Numériques
- Second degré
- Dérivation
- Exponentielle
- Trigonométrie
- Géométrie
- Probas et Stats
- Analyse (spé)
- Géométrie (spé)
- Probabilités (spé)
- Arithmétique (exp)
- Complexes (exp)
- Analyse
- Algèbre
- Analyse
- Algèbre
- Probabilités
SecondePremièreTerminale2BAC SM MarocMPSI/PCSI Physique-Chimie
Physique-Chimie Corrigés de BAC
Corrigés de BAC Révisions Maths lycée
Révisions Maths lycée Prépa Examens
Prépa Examens
Petit problème cercle trigo
Dans cet exercice de trigonométrie, on doit trouver les coordonnées de quatre points d'un carré à partir d'un point donné. Le premier point est donné par ses coordonnées, qui sont liées à la trigo, et se trouve sur le cercle de rayon 1 de centre haut, associé à l'angle pi sur 4. En utilisant la définition géométrique du carré, on peut trouver les coordonnées des autres points en observant que les diagonales se coupent en leur milieu, sont perpendiculaires et ont une même longueur. Pour trouver les coordonnées des points B et D, on ajoute plus pi sur 2 au premier angle, pour obtenir des angles de 3pi sur 4 et 7pi sur 4 respectivement. On peut ensuite lire facilement les coordonnées de ces points sur le cercle trigo en utilisant les valeurs du sinus et du cosinus. En utilisant la caractérisation du carré par ses diagonales, on peut trouver les coordonnées de tous les points du carré.