Cours d'apprentissage en ligne

Intersection de 2 droites

Voici la méthode pour trouver les coordonnées du point d'intersection de deux droites à partir de leurs équations cartésiennes. On résout le système d'équations AX + BY + C = 0 et A'X + B'Y + C' = 0 en trouvant les valeurs de X et Y qui vérifient les deux égalités en même temps. Pour ce faire, on utilise une méthode par combinaison, où on multiplie l'une des équations pour avoir autant de X dans les deux équations et on les soustrait pour faire disparaître les X. On résout ensuite l'équation en Y pour trouver sa valeur, puis on remplace cette valeur dans l'une des équations pour trouver la valeur de X. Les coordonnées du point d'intersection sont alors trouvées. Dans l'exemple donné, les coordonnées du point d'intersection de D1 et D2 sont 2 et moins 2.

Augmentation en pourcentage

Dans cet exercice de calcul de prix, nous devons déterminer le nouveau prix d'une baguette dans une boulangerie suite à une augmentation de 10%. Pour cela, nous utilisons une méthode qui implique de multiplier le prix initial par 1 plus x sur 100, où x est le pourcentage d'augmentation. Dans notre cas, le nouveau prix est de 99 centimes après avoir multiplié le prix initial de 90 centimes par 1,10.

Comprendre le symbole somme

Dans cet exercice, nous apprenons la manière rigoureuse de noter la somme. La notation x1 + x2 +...+ xn n'est pas très rigoureuse, donc nous utilisons le symbole somme, le symbole sigma, pour une notation plus rigoureuse. Nous devons lire cette notation comme la somme de x indices petit i pour i allant de 1 à n. Nous devons écrire la somme de x indice 2i plus 1 pour i qui va de 1 à 8. Pour faire cela de manière rigoureuse, nous pouvons créer un tableau avec les valeurs de i de 1 à 8 et noter l'indice correspondant pour chaque x. Ce qui nous intéresse dans cet exercice est la somme, qui est x3 + x5 + x7 jusqu'à x17.

Comprendre ∩ et ∪

Dans cet exercice sur les probabilités, on manipule les relations entre événements et leurs contraires. On a deux événements S et T, avec P de S égal à 0,5, P de T égal à 0,6 et P de S union T égal à 0,9. On utilise des formules comme P de A inter B, P de A complémentaire, P de A inter B bar et P de A union B bar pour résoudre les questions de l'exercice. On trouve que P de S inter T est égal à 0,2, P de S union T bar est égal à 0,1 et P de S union T est égal à 0,8.

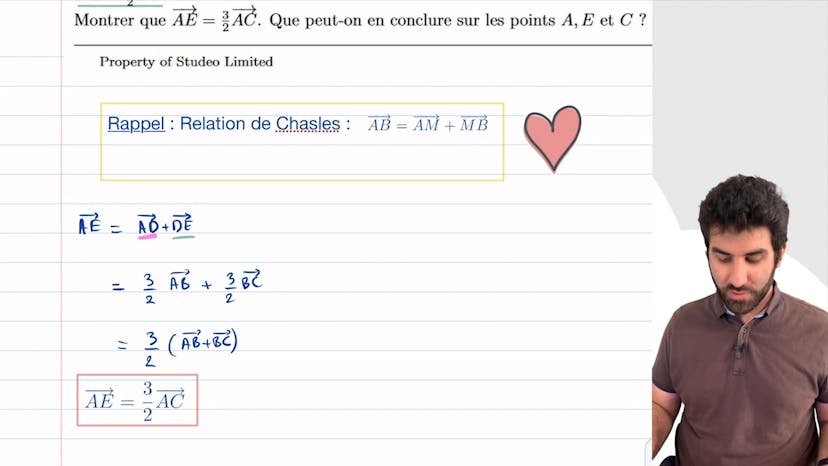
Relation de Chasles

Dans cet exo, on nous donne des relations de vecteurs et on nous demande de conclure sur les points A, E et C. Pour montrer qu'ils sont alignés, on utilise la relation de Schall qui dit qu'un vecteur AB peut être décomposé comme un vecteur AM plus MB pour n'importe quel point M. En utilisant cette relation, on écrit que AE est égal à 3,5 de AC, ce qui signifie que les vecteurs AE et AC sont collinéaires et donc alignés.

Nombres et calculs

Equation produit nul

Dans cet exercice, nous voyons comment résoudre une équation produit nul, c'est-à-dire lorsque le produit de facteur est égal à 0 et qu'au moins un des facteurs est nul. La méthode consiste à regarder chaque facteur et à voir quand il s'annule. Nous appliquons cette méthode à une équation donnée, x²-9 facteur de x plus 20 égal à 0. Nous trouvons que les solutions sont x égale à moins 20, 3 ou moins 3. Nous utilisons également la méthode pour trouver les solutions de x² égale k, ce qui nous permet de trouver les solutions de l'équation de départ. Ainsi, x² moins 9 facteur de x plus 20 est égal à 0 a pour solution moins 20, moins 3 et 3.

Fonction de prix et pourcentage

Dans cet exercice de mathématiques, nous apprenons à généraliser une augmentation de prix de tous les produits d'un magasin. Le gérant du supermarché a décidé d'augmenter tous les prix de 2%. Nous notons x comme le prix d'un produit, f(x) sera le nouveau prix. Pour calculer une augmentation de x%, on multiplie par 1+x/100. Dans ce cas, l'augmentation de 2% est égale à multiplier par 1,02. Donc, f(x) est égale à 1,02x. La méthode générale pour cette augmentation inconnue est représentée par la variable x. L'expression finale est f(x) = 1,02x.

Symétrie centrale

Dans cet exercice de géométrie, on cherche les coordonnées du symétrique d'un point M par rapport à un point I. En utilisant la propriété que le symétrique d'un point par rapport à un autre est le milieu du segment qui les relie, on peut trouver que I est le milieu du segment MM'. En utilisant la formule des coordonnées du milieu, on peut isoler les coordonnées de M' et trouver que XM' est égal à 2X1-X et YM' est égal à 2Y1-Y.

Volumes classiques

Dans cet exercice, nous devons transvaser une sphère remplie d'eau dans un cylindre de base de 4cm de diamètre et de hauteur 4cm. Avant de commencer, nous devons calculer les volumes de la sphère et du cylindre. Le volume d'une sphère de rayon R est de 4/3 π R³, tandis que le volume d'un cylindre de rayon R et de hauteur H est de H x π R². Nous avons donc calculé que le volume de la sphère est d'environ 33,51 cm³ et le volume du cylindre est d'environ 50,26 cm³. Nous cherchons à présent la hauteur à laquelle l'eau remplira le cylindre. Nous avons calculé que la hauteur de l'eau sera de 8/3 cm en égalant le volume de l'eau au volume de la sphère.

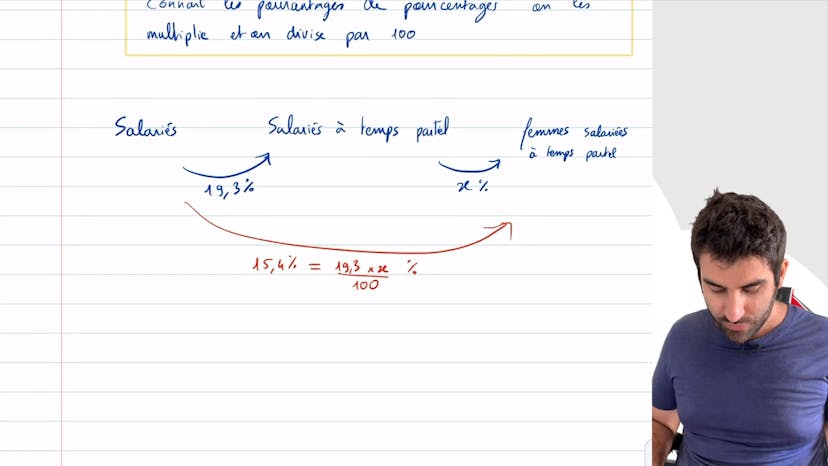
Pourcentage de pourcentage ?

Dans cet exercice, on apprend comment déterminer une proportion de proportions. On applique la méthode qui consiste à multiplier et diviser par 100 pour trouver un pourcentage global en connaissant les pourcentages de pourcentages. On nous donne des informations sur les salariés à temps partiel et les femmes salariées à temps partiel. On apprend que 19,3% des salariés sont à temps partiel et que la proportion de femmes salariées à temps partiel parmi l'ensemble des salariés est de 15,4%. En utilisant la méthode du pourcentage global, on trouve que 15,4% est égal à 19,3 fois x sur 100 pour 100, ce qui permet de résoudre l'équation et d'isoler x. Ainsi, on apprend que parmi les salariés à temps partiel, il y a 70,79% de femmes.

Nombres et calculs

Décomposer en facteurs premiers

Dans cet exercice de décomposition en facteurs premiers, nous allons diviser successivement le nombre 182 952 par tous les nombres premiers. Nous commençons par les plus petits. Nous traçons une ligne pour séparer les nombres trouvés lors de la division et les diviseurs qui nous intéressent. Nous observons que 182 952 est un nombre pair, divisible par 2. Nous écrivons donc 2 x 91 476. Puis, nous divisons 91 476 par 2 pour obtenir 2 x 45 738. Enfin, nous divisons 45 738 par 2 pour obtenir 2 x 22 869. Le chiffre final de 22 869 ne nous permet pas de le diviser par 2, nous testons donc le prochain nombre premier, 3. Nous appliquons le critère de divisibilité par 3, et obtenons 3 x 7623. Nous testons à nouveau le nombre 7623, en appliquant à nouveau le critère de divisibilité par 3, pour obtenir 3 x 2541, puis 3 x 847. Nous testons ensuite si 847 est divisible par 7, en appliquant le critère de divisibilité par 7. Nous séparons le nombre en deux (84 et 7), puis additionnons le premier et le double du second (84 + 7 x 5 = 119). Nous répétons ce critère avec 11 et 9 (11 + 9 x 5 = 56), pour obtenir que 119 est divisible par 7, et donc que 847 est divisible par 7. Nous continuons ainsi la division jusqu'à obtenir que 182 952 est égal à 2 puissance 3 x 3 puissance 3 x 7 x 11 puissance 2, soit la décomposition en facteurs premiers de 182 952.