Cours d'apprentissage en ligne

Images réelles, images virtuelles

Layla de Studio nous parle des relations de conjugaison. Elle aborde les problématiques concernant les lentilles convergentes, la formation d'images et les distances entre les objets et les lentilles. Elle commence par expliquer qu'une lentille convergente a une focale de 10 centimètres et forme une image de hauteur AB égale à 3 centimètres sur un écran. L'objectif est de trouver la position de l'objet par rapport à la lentille, donc la distance OA. Layla rappelle les lois de Newton et de Descartes pour la conjugaison, préconisant d'utiliser la loi de Descartes pour la plupart des exercices. Elle résout ensuite une série de questions, pour lesquelles elle utilise la relation de conjugaison de Descartes pour trouver OA. Elle explique également la formule du grandissement pour déterminer les caractéristiques de l'image. Dans la deuxième question, Layla travaille à partir du grandissement pour trouver les distances OA et OA prime, sachant que AA prime vaut 90 centimètres. Elle utilise ensuite la relation de conjugaison de Descartes pour trouver F prime. Dans la troisième question, elle aborde le cas d'une image virtuelle. Elle explique que l'image virtuelle est située avant la lentille, ce qui signifie que OA' est négatif. Elle utilise le grandissement pour trouver les distances OA et OA'. Enfin, elle répond à une question théorique sur les positions des objets donnant une image virtuelle avec une lentille convergente et divergente. Pour une lentille convergente, l'objet doit se trouver avant le foyer objet F, tandis que pour une lentille divergente, l'objet doit être situé entre la lentille et le foyer objet. En conclusion, Layla a donné un aperçu des relations de conjugaison et des différentes positions d'objets pour obtenir une image virtuelle avec des lentilles convergentes et divergentes. [Number of Words: 383]

Images réelles, images virtuelles

Dans ce cours, nous étudions les relations de conjugaison en optique. Le problème consiste à trouver la position de l'objet par rapport à une lentille convergente. Nous connaissons la distance focale de la lentille (10 cm) et la hauteur de l'image sur l'écran (3 cm). En utilisant les lois de Newton et de Descartes, nous appliquons la relation de conjugaison de Descartes pour trouver la distance OA, qui est -11 cm. En utilisant la formule du grandissement, nous trouvons que l'image est renversée, avec un grandissement négatif et une hauteur de -41 cm. Dans la deuxième partie, nous sommes donnés un rapport de grandissement de 2 pour une lentille mince convergente, avec la seule information donnée étant la distance AA' de 90 cm. En utilisant la relation du grandissement et la relation de Schall, nous trouvons les distances OA (-30 cm) et OA' (60 cm), et en utilisant la relation de conjugaison de Descartes, nous trouvons la distance focale F' de 20 cm. Dans la troisième partie, nous appliquons les mêmes méthodes avec une image virtuelle. Nous trouvons que l'objet doit être situé avant le foyer objet pour obtenir une image virtuelle avec une lentille convergente. Pour une lentille divergente, l'objet doit être situé entre la lentille et le foyer objet. J'espère que ce résumé vous a été utile. N'hésitez pas à poser vos questions en commentaire.

Pouvoir de résolution de l'oeil

Le cours porte sur le pouvoir de résolution de l'œil humain. Il explique que le pouvoir de résolution correspond à l'angle minimal qu'un œil peut voir, et que cette valeur est de 1 minute d'angle. L'angle est ensuite converti en radian pour faciliter les calculs. Le pouvoir de résolution de l'œil est d'environ 3 x 10-4 radian. Le cours explique que le pouvoir de résolution de l'œil est dû au phénomène de diffraction, qui limite la capacité de l'œil à séparer les rayons provenant d'un objet. Le cours présente également un exemple de calcul de la hauteur minimale d'un objet que l'œil peut voir à différentes distances. À une distance de 25 cm, la hauteur minimale est de 0,075 mm. À une distance de 5 m, la hauteur minimale est de 1,5 mm. Et à une distance de 100 m, la hauteur minimale est de 3 cm. Le cours conclut en invitant les étudiants à poser des questions s'ils en ont.

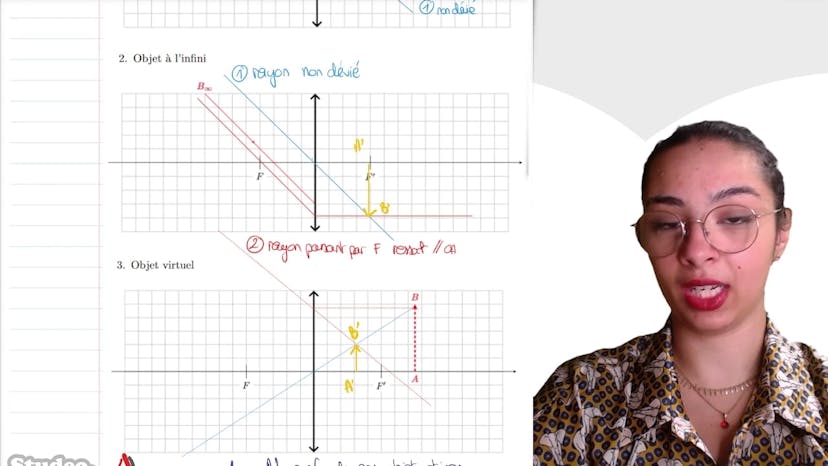
Tracés avec des lentilles convergentes

Le cours porte sur les tracés de rayons en optique. Il est important de bien savoir tracer les rayons pour comprendre les systèmes optiques. Pour cela, il faut s'entraîner à faire différents cas de figures. La première situation présentée est celle d'une lentille convergente avec un objet AB situé entre O et F. Dans ce cas, l'image sera virtuelle et située avant la lentille. Pour tracer les rayons, on utilise le rayon qui passe par le centre de la lentille, qui n'est pas dévié. Ensuite, on peut choisir de tracer le rayon qui passe par le foyer image F' ou le rayon qui passe par F et ressort parallèlement à l'axe optique. En prolongeant ces rayons, on peut déterminer la position de l'image virtuelle. Ensuite, le cours explique comment tracer les rayons lorsque l'objet est à l'infini. Il est important de conserver l'angle que fait l'objet avec l'axe optique. Puisque l'objet est à l'infini, tous les rayons parallèles à celui qui est donné peuvent être tracés. En utilisant le rayon non dévié et en le faisant passer par le plan focal image, on peut déterminer la position de l'image. Le dernier cas étudié est celui d'un objet virtuel, c'est-à-dire un objet situé après la lentille. On commence par tracer le rayon qui passe par le centre optique, qui n'est pas dévié. Ensuite, on peut tracer un rayon qui passe par le foyer image F' et voir où il coupe les autres rayons tracés. La position de l'image virtuelle est donnée par le point de rencontre entre ces rayons. En conclusion, il est essentiel de savoir tracer les rayons en optique pour comprendre les systèmes optiques. En s'entraînant à faire différentes situations, on peut facilement tracer les rayons sans se poser de questions.

Tracés avec des lentilles divergentes

Aujourd'hui, nous allons nous entraîner à tracer les images à travers des lentilles divergentes. Il est primordial de savoir tracer les rayons à travers n'importe quel système de lentilles car cela sera essentiel pour la suite. L'optique se base sur les schémas, donc entraînez-vous au maximum dans différentes situations. Dans la première situation, nous avons un objet situé avant le plan focal objet, ce qui va créer une image virtuelle. Nous commençons par tracer le rayon bleu qui passe par le centre de la lentille et qui n'est pas dévié. Ensuite, nous ajoutons un deuxième rayon pour trouver l'intersection et déterminer l'emplacement de l'image. Par exemple, nous pouvons prendre le rayon vert qui arrive parallèlement à l'axe optique et qui ressort dans le plan focal image. Nous prolongeons ce rayon en pointillé jusqu'à ce qu'il croise le rayon bleu. Une autre possibilité est de prendre le rayon jaune, qui ressort parallèlement à l'axe optique et passe par le foyer objet. Encore une fois, nous prolongeons ce rayon en pointillé et nous voyons que les trois rayons se croisent en un point, indiquant l'emplacement de l'image. Ensuite, nous abordons le cas des objets à l'infini. Dans ce cas, tous les rayons arrivent avec le même angle. Nous prenons un objet B à l'infini et nous pouvons choisir n'importe quel rayon parallèle pour représenter son comportement à travers la lentille. Nous utilisons toujours le rayon bleu qui passe par le centre de la lentille et qui est représenté par trois flèches. Nous savons également que tout objet à l'infini donnera une image dans le plan focal image, qui est perpendiculaire et passe par le foyer principal image. En regardant l'intersection entre le rayon bleu et ce plan, nous pouvons déterminer l'emplacement des images A' et B'. J'espère que cette transcription vous a été utile. N'hésitez pas à poser vos questions ou à faire vos remarques en commentaire.

Téléobjectif

Aujourd'hui, nous étudions le téléobjectif, un exercice courant dans les concours. Le téléobjectif consiste en l'association de deux lentilles, suivi d'un capteur CCD. L'encombrement, c'est-à-dire la distance entre la lentille d'entrée et le capteur, est important car il détermine la taille de l'appareil photo. On cherche donc à réduire cet encombrement tout en maintenant une bonne qualité d'image. Dans la première partie de l'exercice, nous étudions le cas où il n'y a pas de lentilles divergentes. Le grandissement est très faible, ce qui fait que l'image du chamois sur le capteur est très petite. Dans la deuxième partie, nous ajoutons la lentille divergente pour augmenter le grandissement. Cette fois-ci, l'image du chamois sur le capteur est beaucoup plus grande. Enfin, nous calculons l'encombrement total du téléobjectif. Il est important de noter que le choix de la focale influence grandement l'encombrement. En conclusion, cet exercice est utile pour s'entraîner sur les lentilles en vue des concours. N'hésitez pas à poser vos questions en commentaire.

Loupe

Aujourd'hui, nous allons aborder un exercice sur la loupe, un sujet très classique en optique. Les questions sur la loupe font souvent partie des examens et des devoirs. Il existe différentes variations possibles autour de la loupe, il est donc important de consulter les précédents concours pour se préparer. De nos jours, les questions sur l'optique sont plus fréquentes en examens oraux qu'en écrits, mais il est tout de même utile de se familiariser avec le sujet. Dans cet exercice, nous nous intéressons à un œil normal, qui voit distinctement de l'infini jusqu'à une distance minimale appelée DM. L'observateur doit accommoder si l'objet qu'il observe n'est pas à l'infini. L'œil possède un cristallin assimilé à une lentille convergente, qui peut se déformer pour changer sa focale. Lorsque le cristallin se contracte pour changer la focale, on dit qu'il accommode. A priori, le cristallin permet qu'un objet provenant de l'infini atteigne directement la rétine, sans que le cristallin ait à se contracter. Dans cet exercice, nous regardons un petit objet plan ayant une petite longueur L perpendiculaire à l'axe optique. Pour déterminer l'angle maximal sous lequel l'objet peut être vu, nous utilisons le pouvoir de résolution de l'œil, qui est de 310.4 radians. Ensuite, nous nous concentrons sur l'utilisation d'une loupe, qui est une lentille convergente avec une distance focale f'. L'œil se situe à une distance inférieure à la distance minimale à partir de laquelle il peut voir clairement les objets. Nous devons déterminer les positions des objets qui permettent de les observer à travers la loupe. Pour cela, nous utilisons la relation de conjugaison de Descartes en isolant la distance entre la lentille et l'objet (OA'). Nous devons également tenir compte de la distance entre la lentille et l'image (A'). Les objets doivent être placés entre le foyer objet (F') et un point calculé à partir de la distance minimale et de la distance focale (F' * (A-DM) / (F' - A + DM)). Nous effectuons ensuite des constructions géométriques pour illustrer notre résultat. Enfin, nous abordons la question de l'accommodation de l'œil. Lorsque l'image est à l'infini, l'œil n'a pas besoin d'accommoder. Pour atteindre une image à l'infini, l'objet doit être dans le plan focal de la lentille de la loupe. Le grandissement commercial est utilisé pour évaluer la taille de l'objet vu d'un angle donné. Cet exercice est classique et permet de se familiariser avec les notions de grandissement et d'angle de vision pour différents objets et images à travers une loupe. N'hésitez pas à poser vos questions en commentaire.

Lunette astronomique

Aucun résumé n'est disponible pour cette vidéo

Méthode de Bessel

La méthode de vaisselle est une méthode utilisée pour déterminer la distance focale d'une lentille à partir de mesures expérimentales. Cette méthode est souvent utilisée en TP et peut être utile pour répondre à certaines questions dans les concours. La règle des 4 f'' est souvent utilisée pour se référer à cette méthode. Voici comment fonctionne la méthode de vaisselle : On dispose d'une lentille convergente, d'un objet et d'un écran placé à une distance fixe (D) de l'objet. On place la lentille entre l'objet et l'écran et on la déplace pour observer quand l'image de l'objet se forme sur l'écran. La première question consiste à trouver une condition sur D pour laquelle deux positions existent pour la lentille. Cela signifie qu'il est possible de placer la lentille à deux endroits différents entre l'objet et l'écran, et dans ces deux positions, l'image de l'objet se formera sur l'écran. Pour répondre à cette question, on utilise la loi de Descartes qui nous donne l'équation : 1/A' - 1/A = 1/F', où A est la distance entre l'objet et le centre de la lentille, A' est la distance entre l'image et le centre de la lentille, et F' est la distance focale de la lentille. En utilisant cette équation, on obtient un polynôme du second degré (X^2 - DX + DF' = 0) en remplaçant les distances par leurs expressions expérimentales. En calculant le discriminant de ce polynôme (D(D-4F')), on peut déterminer que D doit être supérieur à 4F' pour qu'il y ait au moins deux positions où l'image se forme sur l'écran. Ensuite, on nous demande de relier la distance focale F' avec les distances D et d. Pour cela, on utilise la formule des racines d'un polynôme du second degré pour trouver les valeurs de X1 et X2 (les positions où l'image est nette) : X1 = (-D - √(D(D-4F')))/(2), X2 = (-D + √(D(D-4F')))/(2). En soustrayant ces deux valeurs, on obtient la distance entre les deux positions (d = √(D(D-4F'))). En isolant F' dans cette équation, on obtient F' = (D^2 - d^2)/(4D). En utilisant les valeurs expérimentales données, on trouve que F' = 8 cm. Cette méthode de vaisselle est couramment utilisée et la règle des 4F' est souvent posée sous forme de questions dans les concours. J'espère que cette explication vous a été utile. N'hésitez pas à poser des questions ou à faire des remarques dans les commentaires.

Appareil photo

Dans cette vidéo, Leïla nous présente un cours sur les vidéoprojecteurs. Elle explique que l'objectif est de projeter une pellicule AB sur un écran E à l'aide d'une lentille convergente de distance focale f'. Elle demande aux spectateurs de représenter graphiquement l'image A' et B' de AB en utilisant trois rayons différents. Ces rayons sont le rayon bleu qui passe par le centre de la lentille et n'est pas dévié, le rayon rouge qui arrive parallèlement à l'axe optique et ressort en f', et le rayon qui passe par le foyer objet F et ressort parallèle à l'axe optique. Ensuite, Leïla demande de trouver une condition sur la distance D entre la pellicule et l'écran et la distance focale f' pour que la solution pour la distance d entre la pellicule et la lentille existe. Elle rappelle la méthode de Bessel, où l'on applique les lois de Newton ou de Descartes en utilisant l'équation 1/ D - 1/ d = 1/ f'. La condition pour avoir une solution est que D soit supérieur à 4 f'. Leïla aborde ensuite le grandissement, qui est donné par A'B' / AB, OA' / OA, et OF' / OF. Elle indique que pour avoir un grandissement maximal, il faut que d soit le plus petit possible. Elle utilise ensuite l'équation 1 - D / d pour trouver les valeurs possibles de d, en utilisant la solution la plus petite. Enfin, Leïla effectue une application numérique pour trouver que d et f' sont tous les deux égaux à 19 centimètres. Elle explique que cela est logique car l'écran est situé à une distance infinie par rapport à la lentille. En conclusion, Leïla rappelle que cet exercice est une bonne application de la méthode de Bessel et des relations de conjugaison en optique. Elle encourage les spectateurs à poser leurs questions en commentaire.

Maths

Analyse

Parité

Afin d'optimiser votre texte pour le référencement naturel (SEO), voici le résumé du cours : Dans cette vidéo, Corentin explique un exercice sur les fonctions paires et impaires. Il présente quatre fonctions différentes : un polynôme de degré 4, une fraction rationnelle, une somme de fonctions trigonométriques et une autre fonction trigonométrique. Il rappelle que pour être paire, une fonction doit vérifier que pour chaque x dans son domaine de définition, -x aussi appartient à son domaine, et que f(-x) est égal à f(x). Pour être impaire, la première condition est vérifiée, et en plus f(-x) est égal à -f(x). Il analyse ensuite chaque fonction et détermine si elles sont paires, impaires ou ni l'une ni l'autre. Le polynôme de degré 4 est pair, la fraction rationnelle n'est ni paire ni impaire, la somme de fonctions trigonométriques est impaire, et enfin la dernière fonction trigonométrique n'est ni paire ni impaire. En résumé, le polynôme est pair, la fraction rationnelle n'est ni paire ni impaire, la somme de fonctions trigonométriques est impaire, et la dernière fonction trigonométrique n'est ni paire ni impaire.

Maths

Analyse