Cours d'apprentissage en ligne

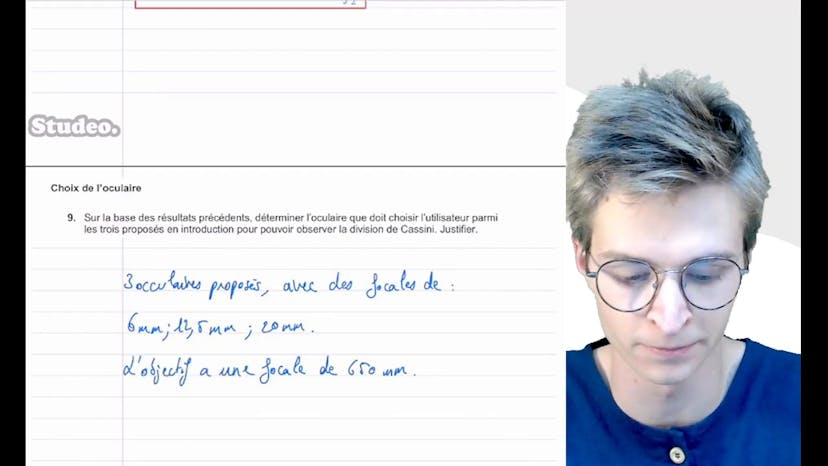
Observation de la division de Cassini (2)

Dans cette vidéo, Théobald de Studio poursuit l'exercice sur l'observation de la division de Cassini avec une lunette astronomique. L'objectif est de déterminer quel oculaire choisir pour observer correctement cette division. Dans la première partie, la lunette est modélisée par un objectif suivi d'un oculaire, avec le plan focal image de l'objectif situé dans le plan focal objet de l'oculaire. Les rayons lumineux traversent les lentilles de la lunette et atteignent la position finale de l'image B'. Il est ensuite expliqué que la lunette est afocale, c'est-à-dire que d'un objet à l'infini, elle donne une image à l'infini. Cela signifie qu'il est possible de regarder à travers la lunette sans avoir besoin d'accommoder, car notre œil regarde naturellement à l'infini. Ensuite, le diamètre apparent de l'angle θ' de l'image θ' à travers la lunette est indiqué sur le schéma. Cela correspond à l'angle sous lequel nous observons l'image B'. Notre œil se place quelque part sur le schéma, et l'angle d'observation est le même que l'angle θ'. La relation entre le grossissement et les distances focales f' et f'' est établie en précisant les étapes. Le grossissement est donné par le rapport θ' sur θ, mais il est nécessaire de déterminer la valeur de θ. En se référant au schéma, θ peut être obtenu en utilisant les angles alternes internes. En utilisant cette relation, il est établi que le grossissement g est égal à f1' divisé par f2'. Ensuite, il est question de choisir entre trois oculaires proposés, avec des focales de 6mm, 12.5mm et 20mm, et un objectif de 650mm. En utilisant la formule du grossissement, un tableau est créé pour calculer le grossissement de chaque oculaire. Il est constaté que l'oculaire 1 avec une focale de 6mm a un grossissement de 108, ce qui est supérieur à 89, donc cela permet d'observer la division de Cassini. Les deux autres oculaires ont des grossissements inférieurs à 89, ce qui signifie qu'ils ne conviennent pas pour observer la division de Cassini. Par conséquent, l'oculaire 1 est choisi. En conclusion, il est recommandé d'utiliser l'oculaire 1 avec une focale de 6mm pour observer correctement la division de Cassini à travers cette lunette.

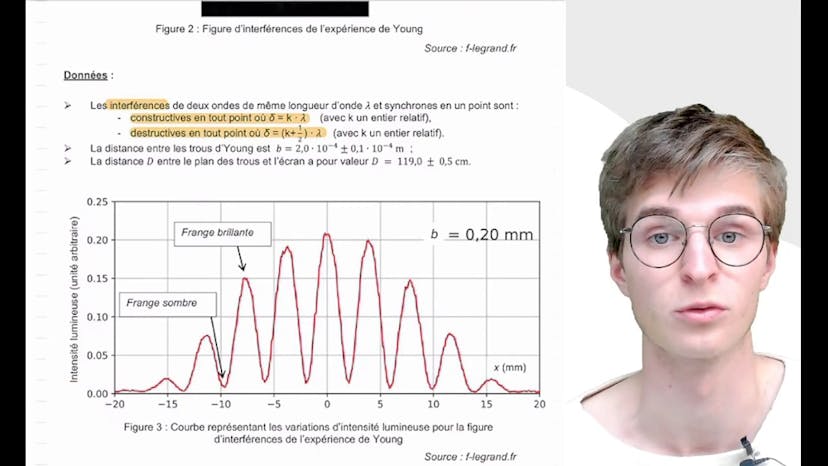
Trous d'Young (1)

Dans cette vidéo, Théobald de Cidéo aborde l'expérience des trous de Yong, un exercice classique en physique. Dans cette expérience, un laser est envoyé à travers un dispositif de trous de Yong, où seuls deux trous permettent au laser de passer. Les ondes laser qui passent par ces deux trous interagissent et créent une figure d'interférence sur un écran situé à une distance D. L'objectif est de trouver la longueur d'onde lumineuse du laser utilisé. Le premier point abordé est la justification de la différence de marge delta en utilisant l'indice de réfraction de l'air, qui est toujours égal à 1. Il est démontré que la différence de marge delta peut être assimilée à S2M moins S1M. Ensuite, Théobald utilise le théorème de Pythagore pour trouver les expressions de S1M² et de S2M² en fonction de D, X et de B sur 2. Il montre également que lorsque D est très grand par rapport à B, S2M² moins S1M² vaut approximativement 2DΔ. À partir de cette équation, il déduit que la différence de marge delta s'écrit Δ = X * B / D. Enfin, il aborde les interférences lumineuses et montre que X est égal à kλD / B pour les points où M est situé à un maximum d'intensité d'une frange brillante, où k est un entier et λ est la longueur d'onde. Le cours se termine en indiquant que la suite de l'exercice sera abordée dans une autre vidéo.

Trous d'Young (2)

Dans cette vidéo, on analyse la figure d'interférence des trous de Young pour déterminer la longueur d'onde du laser utilisé. On établit l'expression de l'interfrange Y en fonction de λB et D. On mesure graphiquement la valeur de Y en prenant en compte les périodes spatiales. On trouve que Y vaut 3,9 mm. En utilisant la formule Y = λD/B, on déduit que la longueur d'onde λ vaut environ 660 nm. Cependant, il faut prendre en compte les incertitudes dans l'expérience. On calcule les incertitudes relatives U de B, U de I et U de D. On obtient U de lambda, qui est de l'ordre de 10^-8 mètres. L'incertitude absolue doit être du même ordre de grandeur que le dernier chiffre significatif de la longueur d'onde, soit 10^-8 mètres également. Ainsi, la longueur d'onde λ vaut 660 +/- 40 nm. Les lasers pouvant être utilisés dans cette expérience sont ceux ayant une longueur d'onde entre 620 et 700 nm, notamment le rouge A (630 nm), le rouge B (650 nm) et le rouge C (694 nm). Cependant, il n'est pas possible de discriminer plus précisément entre ces lasers avec les instruments de mesure utilisés.

Télémètre à ultrasons (1)

Le cours traite du principe des incertitudes dans le domaine de la physique, en se concentrant sur l'utilisation d'un télémètre à ultrasons. Le télémètre envoie des ultrasons qui se réfléchissent sur un objet et reviennent vers le récepteur, permettant de déterminer la position de l'objet en mesurant la durée du trajet des ultrasons. La distance entre le télémètre et l'objet est supposée être beaucoup plus grande que la distance entre l'émetteur et le récepteur, ce qui permet de supposer que les ultrasons se déplacent en ligne droite sur l'axe O-X. Le cours présente un extrait de code Python qui traite les données du microcontrôleur relié au télémètre et permet de calculer la distance X à partir de la durée Δt mesurée. Le calcul de la distance X est effectué en multipliant la vitesse de propagation des ultrasons par la durée Δt et en divisant le tout par 2. Le cours explique également que la vitesse de propagation des ultrasons doit être calibrée, car elle dépend de la température de l'air. Un protocole expérimental est proposé pour calculer cette vitesse en mesurant la distance X et en utilisant les durées Δt fournies par l'ordinateur. En répétant ce processus pour différentes valeurs de X, on peut obtenir plusieurs valeurs de la vitesse de propagation et calculer leur moyenne pour calibrer le télémètre. Le cours conclut en mentionnant que la prochaine vidéo abordera le calcul et la mesure des incertitudes.

Télémètre à ultrasons (2)

Dans cette vidéo, Obel2 Studio continue la correction de l'exercice sur le télémètre à ultrasons et les incertitudes de mesure. Le protocole expérimental consiste à mesurer la vitesse des ultrasons en utilisant Δt, le temps de mesure donné. On fait plusieurs mesures de VS en plaçant toujours l'obstacle au même endroit. On utilise des astuces pour gérer les incertitudes. On calcule VSI pour chaque XI et Δti, puis on mesure VSI plusieurs fois pour éviter les problèmes d'incertitude. Ensuite, on fait la moyenne des mesures de VS pour obtenir une valeur précise. Pour calculer la valeur moyenne de VS avec les incertitudes et les bonnes chiffres significatifs, on utilise l'incertitude de type A, qui est σ sur racine de n. Ensuite, on calcule la moyenne des mesures de VS. Pour l'incertitude de type A, on utilise σ=0,9. On obtient donc VS moyen = 349,4 +/- 0,9 m/s. Pour la question suivante, on modifie la valeur v dans le code Python pour tenir compte de la valeur moyenne de VS (349,4 m/s). Ensuite, on nous donne l'incertitude delta t = 10 μs et la mesure delta t mesuré = 3438 μs. On doit calculer la valeur de x en tenant compte des incertitudes associées. On utilise la formule x = x mesuré + incertitude de calcul de x. On calcule x mesuré en utilisant VS, delta t et on obtient 6,006 x 10-1 m. L'incertitude de calcul de x est calculée en utilisant les incertitudes relatives de VS et delta t, ce qui donne une incertitude de 0,01 m. Donc, x = 6,0 +/- 0,1 x 10-1 m, soit 60 cm. La vidéo se termine en annonçant la deuxième partie de l'exercice et en invitant les spectateurs à poser des questions.

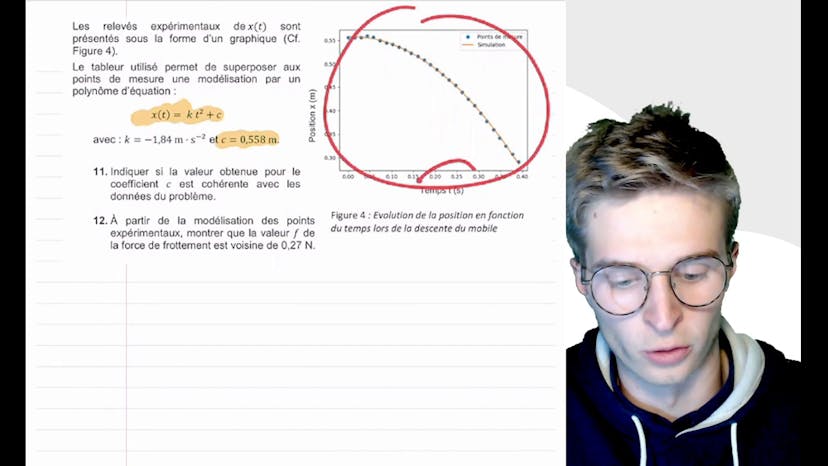
Télémètre à ultrasons (3)

Bonjour à tous, dans cette vidéo, nous allons corriger un exercice de mécanique qui concerne un système composé d'une voiture lâchée sans vitesse initiale sur une pente inclinée. On nous dit que dans le référentiel terrestre, la voiture est soumise au poids, à la réaction du support et aux forces de frottement opposées au mouvement. La première question consiste à déterminer la direction et le sens du vecteur accélération, qui va des X positifs vers les X négatifs. La deuxième loi de Newton est ensuite énoncée, indiquant que la somme des forces extérieures est égale à la dérivée du vecteur quantité de mouvement. Du principe fondamental de la dynamique, on déduit que la somme des forces extérieures et l'accélération ont la même direction et le même sens. Ensuite, on étudie le mouvement du centre de masse du système selon l'axe ox. En utilisant la deuxième loi de Newton, on montre que l'équation horaire du mouvement est de la forme moins un demi de F sur m fois t² plus X0. On nous donne ensuite des relevés expérimentaux de la position en fonction du temps, qui ont été modélisés par une équation polynomiale. On nous demande si la valeur du coefficient c dans cette équation est cohérente avec les données du problème. En identifiant c avec X0, il s'avère que la valeur obtenue pour le coefficient c est effectivement cohérente avec les données du problème. Enfin, à partir de la modélisation des points expérimentaux, on montre que la valeur de la force de frottement est voisine de 0,27 N. On utilise l'expression de la résultante des forces pour exprimer la force de frottement en fonction du coefficient de la modélisation, et on obtient ainsi la valeur de la force de frottement recherchée. La suite de l'exercice sera abordée dans une prochaine vidéo.

Télémètre à ultrasons (4)

Dans cette vidéo, Théobald de Studio fait une étude énergétique d'un système mécanique. Il commence par rappeler le théorème de l'énergie cinétique, qui énonce que la variation de l'énergie cinétique d'un système entre deux états est égale à la somme des travaux des forces exercées sur l'objet. Ensuite, il calcule le travail de la force de frottement entre les points A et B, en utilisant la relation WAB = f * d, où f est la force de frottement et d est la distance entre les deux points. Il calcule également le travail du poids, qui est égal à M * g * Sin(α) * d, où M est la masse, g est l'accélération due à la gravité, et α est l'angle de la pente. Il souligne que la réaction du support n'effectue aucun travail car elle est perpendiculaire au mouvement. En utilisant le théorème de l'énergie cinétique, Théobald trouve une nouvelle estimation de la force de frottement en égalant le travail total aux variations d'énergie cinétique entre les points A et B. Il obtient l'expression suivante : f = (1/2) * (M * Vb^2) - (M * g * Sin(α)), où Vb est la vitesse au point B. Il effectue ensuite les calculs numériques, avec une valeur de Vb de 1,21 m/s, et obtient une valeur pour f de 0,29 N. En conclusion, Théobald explique une astuce pour calculer rapidement le produit scalaire entre deux vecteurs. Si les forces sont dans le même quart de plan et tirent dans le même sens, le produit scalaire est la multiplication des normes des forces par le cosinus de l'angle entre elles, avec un plus devant. Si les forces ne sont pas dans le même quart de plan, le produit scalaire est la multiplication des normes des forces par le sinus de l'angle entre elles, avec un moins devant. Il encourage les spectateurs à utiliser cette astuce pour éviter des erreurs fréquentes dans les calculs de produits scalaires. Note : La transcription a été générée automatiquement et pourrait contenir des erreurs.

L’acide formique pour stocker le dihydrogène (1)

Dans cette vidéo, Théobald de Cydéo explique comment l'acide formique peut être utilisé pour stocker du dihydrogène. Le dihydrogène est inflammable à température ambiante, il n'est donc pas pratique à stocker. Cependant, le dioxyde de carbone peut réagir avec le dihydrogène pour former de l'acide formique, qui est peu inflammable. Les chercheurs de l'université de Rice ont développé un procédé catalytique pour produire de l'acide formique. Dans la première partie de l'exercice, on justifie que l'acide formique est également appelé acide métanoïque dans la nomenclature officielle. Ensuite, on vérifie qu'un litre de dihydrogène à une pression de 300 bar et une température de 25°C contient une masse de 28 g de dihydrogène en utilisant la loi des gaz parfaits. On explique ensuite comment récupérer le dihydrogène à partir de l'acide formique grâce à une transformation chimique totale. On vérifie que 1 litre d'acide formique permet de produire 53 g de dihydrogène, comme indiqué dans le document 1. De plus, on mentionne deux avantages de l'acide formique par rapport au stockage du dihydrogène sous pression : sa faible inflammabilité à température ambiante et sa plus grande capacité de stockage par rapport au dihydrogène pur pressurisé.

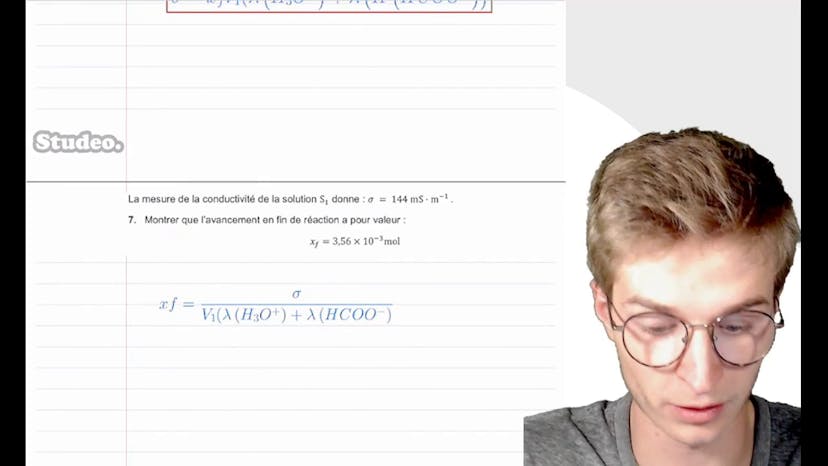
L’acide formique pour stocker le dihydrogène (2)

Dans cette vidéo, Theobald de Cidéo nous présente un exercice de chimie portant sur une méthode conductimétrique pour contrôler la teneur en acide formique d'une solution aqueuse. La première partie de l'exercice nous rappelle que l'acide formique est une bonne solution pour stocker le dihydrogène. L'objectif maintenant est donc de contrôler la teneur en acide formique d'une solution aqueuse préparée par des chercheurs de l'Université de Reuss. Pour cela, on dilue 100 fois une solution aqueuse S0 d'acide formique pour obtenir une solution S1 de concentration C1. On prélève ensuite un volume V1 de cette solution pour mesurer sa conductivité. Pour exprimer la conductivité sigma de la solution, on utilise la formule de la conductivité qui est la somme des conductivités ioniques molaires des ions oxynium et des ions formiate, multipliée par leurs concentrations respectives. On néglige ici l'autoprotolyse de l'eau. Ensuite, on nous demande de déduire une relation entre la conductivité sigma, les conductivités molaires ioniques lambda H3O+ et lambda HCO- et le volume V1. On utilise le tableau d'avancement pour montrer que sigma est égale à la concentration d'ions H3O+ multipliée par la conductivité molaire des ions H3O+, plus la concentration d'ions formiate multipliée par la conductivité molaire des ions formiate. L'exercice suivant consiste à montrer que l'avancement en fin de réaction XF est égal à 3,56 x 10-3 mol. Pour cela, on utilise la mesure de la conductivité de la solution (144 mSqm) et on isole XF dans la formule. On trouve alors XF en fonction de sigma et on effectue le calcul numérique pour obtenir la valeur de XF. Ensuite, on introduit la constante d'équilibre Ka et on montre qu'elle peut s'écrire en fonction de XF, V1 et C1. On isole C1 dans la formule pour déterminer la concentration molaire de la solution S1 utilisée pour la conductimétrie. On effectue le calcul numérique pour obtenir la valeur de C1. Ensuite, on déduit la concentration molaire de la solution mère S0 en utilisant la dilution de 100 fois de S0 pour obtenir S1. On trouve que la concentration de S0 est environ égale à 7,16 mol par litre. Enfin, on compare qualitativement la concentration obtenue avec la teneur en acide formique annoncée dans le document 2. On constate que la concentration obtenue (7,16 mol par litre) est en accord avec celle mentionnée dans le document 2 (7,0 mol par litre). Il s'agit du résumé en SEO friendly de ce cours.

Savon de Marseille (1)

Dans cet exercice, il est question de la saponification, qui est la réaction permettant de créer du savon. L'objectif est de créer un savon de Marseille en faisant réagir de l'huile d'olive avec de la soude. Le cours aborde différents aspects de cette réaction. Tout d'abord, on nous demande d'analyser la formule chimique de l'oléine pour justifier qu'il s'agit d'un triester. On observe que l'oléine contient trois groupes fonctionnels ester, ce qui en fait bien un triester. Ensuite, on nous demande de citer deux règles de sécurité liées à l'utilisation de la soude concentrée. On explique que la soude est corrosive et peut causer des irritations et des brûlures. Il est donc nécessaire de prendre des précautions et de travailler sous une hotte aspirante pour éviter les vapeurs irritantes. Une hypothèse est demandée sur le rôle de l'éthanol dans la réaction. On analyse le protocole expérimental et constatons que l'oléine n'est pas soluble dans l'eau, contrairement à l'hydroxyde de sodium. En revanche, l'oléine et la soude sont tous deux solubles dans l'éthanol. Ainsi, l'éthanol sert de solvant pour permettre à l'oléine et à la soude de réagir ensemble. Un argument est ensuite demandé pour expliquer pourquoi l'ion oléate prédomine par rapport à l'acide oléique. On observe que la présence de l'hydroxyde de sodium, une base forte, dans la réaction rendra la solution basique. Cela place le pH au-dessus du pKa de l'acide oléique, ce qui favorise la prédominance de l'ion oléate. On nous demande ensuite de préciser le rôle du chauffage dans la réaction. Le chauffage permet d'accélérer la réaction en augmentant la température, qui est un facteur cinétique. Il existe également d'autres facteurs cinétiques tels que la pression et la concentration. Enfin, on explique pourquoi de l'eau salée est utilisée plutôt que de l'eau douce dans la phase de relargage. L'objectif de cette phase est de séparer l'oléate de sodium du glycérol. En utilisant de l'eau salée, qui a une solubilité différente de l'eau douce, on peut empêcher l'oléate de sodium de passer dans la phase aqueuse, permettant ainsi de séparer les deux produits. Il est important de prendre en compte que ce texte est une transcription d'une vidéo et peut nécessiter certaines modifications pour être pleinement SEO friendly.

Savon de Marseille (2)

Dans cette vidéo, Théobald de Studio aborde la réaction de saponification, qui permet d'obtenir du savon à partir d'un corps gras et de soude. Il explique que l'huile d'olive, principalement constituée d'oléine, et la soude, hydroxyde de sodium, sont les réactifs utilisés. En les faisant réagir, il obtient de l'oléade de sodium et du glycérol. Il présente ensuite le protocole expérimental, qui consiste à montrer que l'oléine est le réactif limitant. Il explique comment calculer la quantité de matière de l'oléine à partir de sa masse et de sa masse volumique. Il fait de même pour la soude. Il souligne également l'importance d'éliminer le réactif en excès, en l'occurrence la soude, par le lavage, pour éviter d'avoir un savon corrosif. Il précise que le glycérol peut également être éliminé lors du lavage. 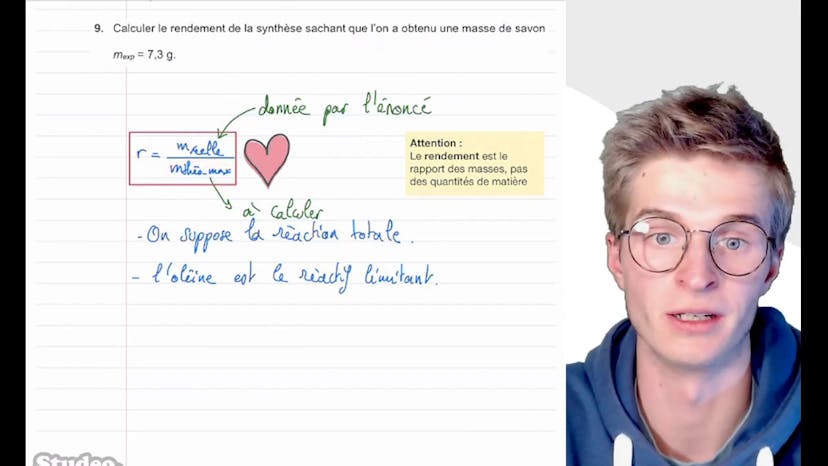Ensuite, il demande de calculer le rendement de la synthèse du savon, en utilisant la masse réelle du savon obtenue et la masse théorique calculée en supposant une réaction totale. Il insiste sur le fait que le rendement est un rapport de masse et non de quantité de matière. Enfin, il propose une hypothèse pour expliquer pourquoi le rendement n'est pas de 100%. Il explique que pour avoir un rendement de 100%, il faudrait une réaction totale, ce qui est rare. Il suggère également que des erreurs de manipulation peuvent être responsables d'un rendement inférieur à 100%. En conclusion, Théobald explique que le rendement de la synthèse du savon est de 80% et encourage les spectateurs à poser des questions s'ils en ont. Il termine en souhaitant bonne chance pour les révisions.