Cours d'apprentissage en ligne

Determiner une asymptote + étude

Dans ce cours, nous apprenons comment trouver les asymptotes d'une fonction. Les asymptotes peuvent être situées à moins l'infini, à plus l'infini, à la fois à moins l'infini et à plus l'infini, ou sur les bords de l'ensemble de définition de la fonction, là où il y a des valeurs interdites. Dans l'exemple donné, la fonction f(x) = -2/(1-x) est définie sur R privé de 1. Nous examinons les cas de moins l'infini et plus l'infini. Quand x tend vers moins l'infini, 1-x tend vers plus l'infini, et quand x tend vers plus l'infini, 1-x tend vers moins l'infini. Par quotient, nous concluons que f(x) tend vers moins l'infini en 0 et vers plus l'infini en 0. Nous en déduisons alors que la courbe CF a pour asymptote horizontale la droite d'équation y = 0, à moins et plus l'infini. Ensuite, nous examinons ce qui se passe en 1. Quand x tend vers 1 par valeur inférieure, 1-x tend vers 0 plus, et quand x tend vers 1 par valeur supérieure, 1-x tend vers 0 moins. Afin de confirmer cette tendance, nous pouvons choisir une valeur inférieure à 1, comme 0.1, où 1-0.1 est positif. Ainsi, 1-x tend vers plus l'infini en 1 par valeur inférieure. Nous pouvons également choisir une valeur supérieure à 1 pour vérifier. De ce fait, par quotient et en tenant compte du facteur -2, nous concluons que f(x) tend vers moins l'infini en 1 par valeur inférieure et vers plus l'infini en 1 par valeur supérieure. Lorsqu'il y a une valeur interdite, cela indique généralement une tendance vers plus ou moins l'infini, et nous avons alors une asymptote verticale. Ici, en x = 1, nous avons donc une asymptote verticale d'équation x = 1. En résumé, pour trouver les asymptotes, nous regardons les tendances en plus l'infini, moins l'infini et sur les bords de l'ensemble de définition de la fonction. Je recommande de vous entraîner à ces calculs et si vous avez des questions, consultez la FAQ.

Calcul de limite infinie avec la définition (trouver un A)

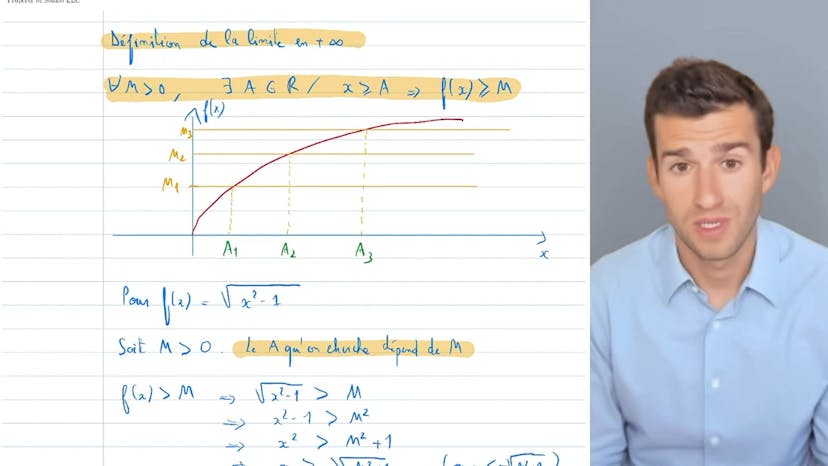
La limite est définie comme étant lorsque une fonction tend vers l'infini. Peu importe la hauteur fixée, il y aura toujours un moment où la fonction la dépassera et sera au-dessus. Pour montrer cela, nous pouvons tracer des graphiques et fixer des valeurs pour m. A partir de ces valeurs, nous pouvons trouver les points où la fonction est toujours au-dessus de la hauteur fixée. Dans cet exemple, nous avons tracé une fonction racine de x et fixé différentes valeurs pour m. Nous pouvons constater que peu importe la valeur de m, il existe toujours un réel a où la fonction est au-dessus de la hauteur fixée. Ensuite, nous passons à un autre exemple où f(x) est égale à la racine de x carré moins 1. Pour montrer que la limite de cette fonction tend vers l'infini, nous devons trouver la valeur de a en résolvant l'inéquation f(x) > m. Nous trouvons a = racine de m carré plus 1. En utilisant cette valeur de a, nous pouvons montrer que si x est supérieur à a, alors f(x) sera supérieur à m. Il est important de s'exercer avec différentes fonctions pour pratiquer cette méthode et trouver les bonnes valeurs de a. En fin de compte, il s'agit simplement de résoudre des équations. C'est ainsi que nous revenons à la définition formelle de la limite.

Calcul de limite finie avec la définition (trouver un epsilon)

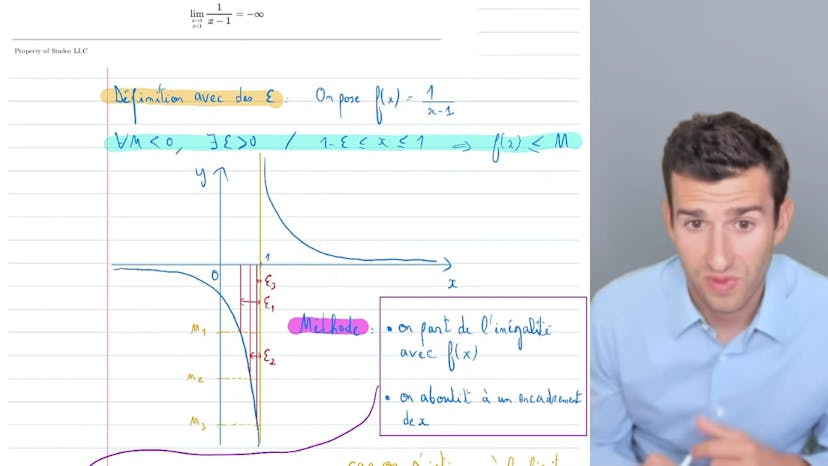
La méthode que nous allons utiliser pour le calcul de la limite finie consiste à utiliser la définition formelle de la limite avec les epsilon. En utilisant cette méthode, nous pouvons montrer que la fonction tend vers moins l'infini. Nous fixons un réel et nous choisissons une limite aussi basse que nous le souhaitons. Nous cherchons ensuite une valeur négative pour laquelle la fonction sera inférieure à cette limite. Nous trouvons un intervalle du type 1-epsilon1, où la fonction est inférieure à M1. Nous pouvons faire la même chose avec d'autres valeurs de M pour obtenir d'autres intervalles. La méthode consiste à partir de l'inégalité f(x) inférieure à M, à résoudre f(x)-M et à trouver un encadrement de x qui nous permet de trouver l'epsilon correspondant. Nous prenons un réel M négatif, nous regardons la limite en 1- et nous résolvons f(x)-M, ce qui nous donne l'encadrement de x. Nous trouvons ensuite l'epsilon en utilisant cet encadrement. En résumé, nous utilisons la méthode de l'encadrement pour trouver l'epsilon correspondant en partant de l'inégalité f(x) inférieure à M. Nous trouvons ainsi rigoureusement que la limite quand x tend vers 1- est moins l'infini. Il est important de s'exercer avec d'autres exemples pour bien comprendre cette méthode.

Utilisation de la dérivée

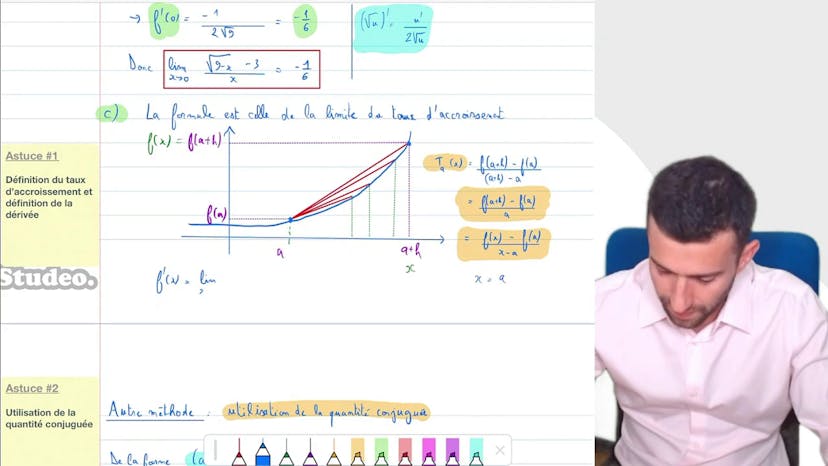
Dans cet exercice, nous devons trouver la limite d'une fonction en utilisant la dérivée. L'énoncé contient plusieurs exemples de ce type de problème. La première étape consiste à repérer les limites à calculer. Ensuite, nous utilisons la définition du taux d'accroissement pour réécrire la limite en utilisant la dérivée de la fonction. Ensuite, nous calculons la dérivée de la fonction et évaluons la dérivée en un point donné. Enfin, nous obtenons la limite en utilisant la dérivée calculée. Dans certains cas, il est possible d'utiliser une autre technique, comme la multiplication par la quantité conjuguée, pour lever l'indétermination de la limite. Il est important de vérifier si la limite est indéterminée au préalable. En utilisant ces méthodes, nous pouvons trouver les limites des fonctions données. Si des questions subsistent, il est possible de poser des commentaires dans la FAQ.

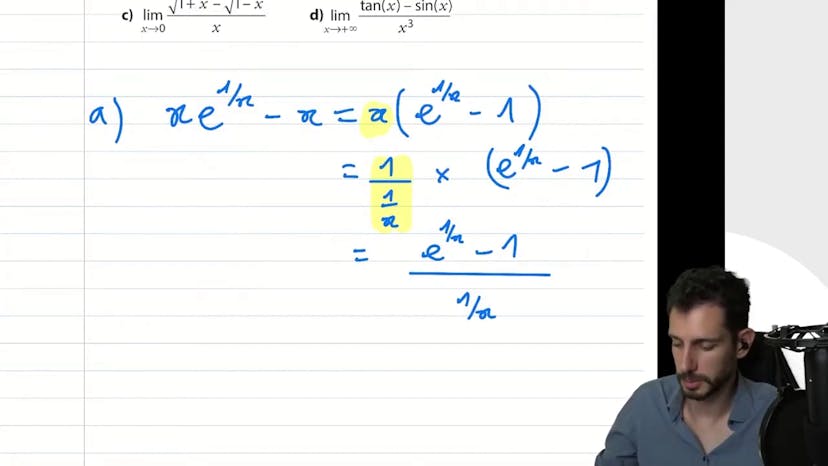
Encore un taux d'accroissement de exp

Ce cours porte sur le calcul de limites, avec un exemple particulièrement difficile : la limite de la fonction x exposant 1 sur x, moins x. Lorsque x tend vers l'infini, la fonction tend vers 1. Pour simplifier l'expression, on factorise par x, ce qui donne e de 1 sur x, moins 1. Cependant, cette simplification ne permet pas de résoudre l'indétermination de la forme. On utilise donc une astuce en posant x égal à 1 sur 1 sur x, ce qui donne e de quelque chose tendant vers 0, moins 1 sur quelque chose tendant vers 0. Cette limite est déjà connue et égale à 1. Ainsi, la limite de la fonction initiale est également égale à 1. Ce type d'exercice demande de repérer les formules et connaissances mathématiques spécifiques, afin de les appliquer de manière astucieuse pour obtenir la solution.

Introduction Convergence

Dans ce nouveau sous-chapitre sur les limites de fonctions, nous abordons des concepts plus pratiques et concrets. Il est important de connaître par cœur certains tableaux de fonctions de référence, par exemple la limite de 1 sur x en plus infini. Nous étudions également comment combiner des limites, par exemple la limite de f plus g. Certaines situations, comme lorsque f tend vers plus infini et g tend vers moins infini, nécessitent une étude plus approfondie. Nous examinons le rapport f sur g et le produit f fois g, en appliquant des règles spécifiques. Il y a quatre formes indéterminées pour lesquelles il n'y a pas de règles préétablies. Nous abordons également les théorèmes de convergence, tels que le théorème des gendarmes, dans lequel deux fonctions encadrent une troisième fonction pour la mener vers la même limite finie. Le théorème de comparaison est utilisé pour les limites infinies, où si une fonction f est inférieure à une fonction g et que f tend vers plus infini quelque part, g la suit également. Nous parlons également de la croissance comparée, en se concentrant sur l'exponentielle et discutons de la limite de composé, qui permet de gérer des fonctions complexes. Il faut également connaître les tableaux de référence pour les fonctions de référence, les opérations sur les limites et les quatre formes indéterminées. En termes de méthode, nous apprenons à gérer les formes indéterminées en utilisant des techniques telles que le terme du plus haut degré et la méthode de quantité conjuguée. En conclusion, en maîtrisant ces points de cours et les méthodes associées, vous serez prêts à aborder les différentes limites qui vous seront présentées. N'hésitez pas à poser des questions dans la FAQ si nécessaire.

Tableaux : fonctions de référence

Dans cette vidéo, nous faisons un bilan des différentes fonctions de référence et de leurs limites, ainsi que des règles de combinaison de ces limites. Nous commençons par étudier la fonction 1/x. La limite de cette fonction est plus l'infini lorsque x tend vers 0 à partir de valeurs positives, et moins l'infini lorsque x tend vers 0 à partir de valeurs négatives. Ensuite, nous examinons les limites de la fonction x^n, où n est un nombre entier. Lorsque x tend vers plus l'infini, cette fonction tend également vers plus l'infini. Si n est pair, la fonction reste positive quel que soit x. Si n est impair, la fonction change de signe selon le signe de x. Nous parlons ensuite des fonctions exponentielles et racines. L'exponentielle de x tend vers plus l'infini lorsque x tend vers plus l'infini, et vers 0 lorsque x tend vers moins l'infini. L'exponentielle de -x est symétrique par rapport à l'axe des ordonnées. La racine de x tend vers 0 en plus l'infini, et 1 sur la racine de x tend vers 0 en plus l'infini également. En conclusion, il est important de comprendre ces différentes fonctions et leurs limites pour résoudre des exercices de calcul.

Tableaux : combiner des limites

La prochaine étape consiste à étudier les limites des fonctions, notamment les limites d'une somme et d'un produit. Il existe plusieurs cas simples à prendre en compte. Lorsque deux fonctions, f et g, tendent chacune vers une limite L et L', respectivement, la limite de leur somme est L + L' et la limite de leur produit est L * L'. Ensuite, si L est une limite finie et qu'il est ajouté ou soustrait à une limite infinie, c'est toujours l'infini qui l'emportera. Pour le produit, cela dépendra du signe de L. Si L est positif, la limite tendra vers l'infini inversé, alors que si L est négatif, la limite tendra vers l'infini. Il faut garder à l'esprit que ces exemples suivent des règles de signes : plus et plus font plus, plus et moins font moins, et moins et moins font plus. Les cas où il est écrit "fi" représentent des cas indéterminés, c'est-à-dire des situations où il est impossible de déterminer la limite. Ces cas incluent la multiplication de 0 par l'infini et l'addition de plus l'infini et moins l'infini. Une forme indéterminée signifie qu'il n'y a pas de règle générale qui s'applique dans toutes les situations. Pour illustrer cela, prenons l'exemple de l'addition de plus l'infini et moins l'infini. Selon les fonctions choisies, comme x, x^2 et x, les résultats peuvent varier et seront sans rapport les uns avec les autres. C'est ce qui rend une forme indéterminée : il n'y a pas de résultat prédéterminé, tout peut se produire. En ce qui concerne le quotient, si l'on divise deux fonctions f et g, on obtient une limite l sur l'axe des x et L' sur l'axe des y, si f et g tendent respectivement vers L et L'. Il existe des règles évidentes à suivre : si la limite de f est L et la limite de g tend vers l'infini, le résultat sera très grand, donc la limite sera de 0. Si la limite de f est L et la limite de g est 0, le résultat sera plus ou moins l'infini, comme nous l'avons déjà vu avec l'exemple de 1/x. En conclusion, il existe deux formes indéterminées à retenir : 0 sur 0 et plus l'infini sur plus l'infini. Ces formes indéterminées peuvent donner différents résultats selon les fonctions choisies. Il est important de s'entraîner à créer des exemples simples pour bien comprendre ces concepts. Il est également crucial de se rappeler que les formes indéterminées signifient qu'il n'y a pas de règle générale, et que tout est possible. En résumé, les formes indéterminées sont les aspects les plus importants à retenir lors de l'étude des limites des fonctions.

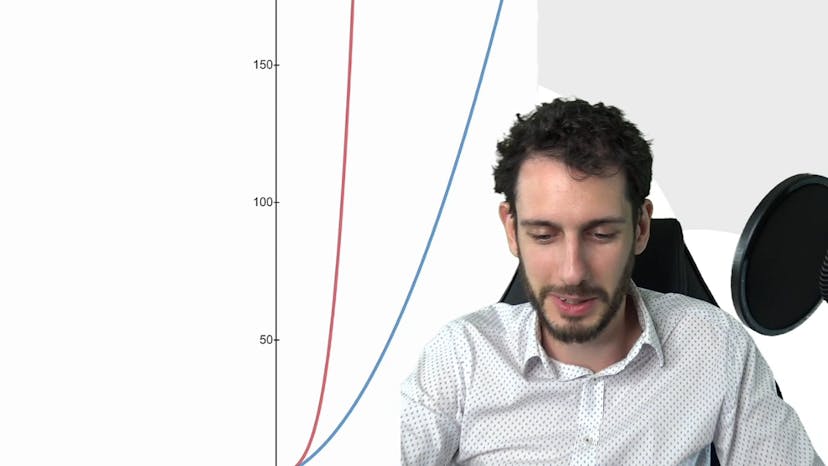
Comparaison et encadrement

Le cours résume les deux théorèmes de comparaison et d'encadrement pour les fonctions. Le premier théorème stipule que si deux fonctions f et g tendent vers plus l'infini et que g est plus grande que f, alors f va pousser g vers plus l'infini. Le deuxième théorème, appelé théorème des gendarmes, dit que si f et h encadrent une fonction g et que f et h tendent vers la même limite, alors g tend également vers cette limite. Des exemples graphiques ont été donnés pour illustrer ces théorèmes.

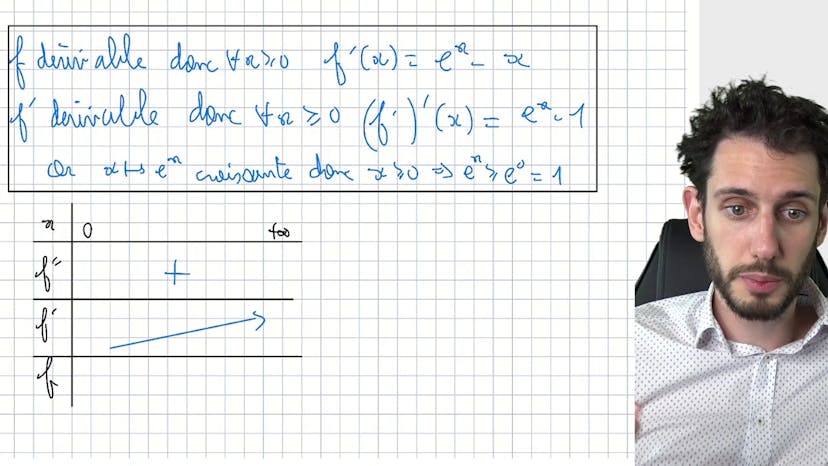
Croissance comparée exp et ln

Dans ce sous-chapitre sur les limites de fonctions, il est abordé le concept de croissance comparée. En résumé, la croissance comparée est l'idée que la fonction exponentielle domine n'importe quelle puissance de x. Cela signifie que quand on divise l'exponentielle e^2x par x^n, la limite de cette expression tend vers l'infini. La possibilité d'utiliser cette propriété est démontrée en montrant que la fonction f(x) = e^2x - (x^2)/2 est toujours positive. En utilisant cette démonstration, on peut alors prouver que e^x/x^n tend vers l'infini. De plus, il est également démontré que e^(-x)/x^n tend vers 0 quand x tend vers moins l'infini. Ces démonstrations utilisent des changements de variables simples pour simplifier les expressions et appliquer les propriétés des puissances. Il est souligné que ces méthodes peuvent être utiles non seulement dans le contexte de ces démonstrations, mais aussi dans d'autres calculs de limites ou exercices.

Limite des fonctions composées

Le cours porte sur les limites de fonctions, en se concentrant sur le concept de composition. Le professeur donne un exemple concret et simple pour illustrer l'idée de composition. Il explique que la composition consiste à décomposer une fonction en plusieurs morceaux et montre comment cela s'applique à l'exemple donné. Il souligne également l'importance de démontrer les résultats obtenus par composition, en ajoutant que cela nécessite une autorisation théorique. Il promet de revenir sur cette notion plus tard. En résumé, le cours met en avant l'idée de composition dans le calcul des limites de fonctions et explique comment appliquer cette notion à un exemple spécifique. Note de l'éditeur : Pour optimiser ce résumé pour le référencement SEO, il serait nécessaire de le réorganiser afin de mettre l'accent sur les mots-clés pertinents pour le contenu donné. Cela pourrait inclure des mots-clés tels que "limites de fonctions", "composition", "démontrer les résultats", "autorisation théorique", etc.