Online Induction course by Top Instructors - Induction

Courant induit

Aucun résumé n'est disponible pour cette vidéo

Rotation de spire

Aucun résumé n'est disponible pour cette vidéo

Dans cette vidéo, nous examinons le mouvement d'un aimant droit de moment magnétique M, dont le pôle nord est orienté vers un circuit. Le circuit est composé d'une spire de rayon A, de centre O, d'axe OZ assimilable à une résistance R. L'aimant glisse le long de l'axe OZ à une vitesse constante V0. Le champ magnétique créé par l'aimant à une distance Z sur l'axe est donné par l'expression B = (-μ0M)/(2πZ^3). Le sens du courant d'intensité I est déterminé par l'orientation de la surface DS. Lorsque l'aimant recule, le flux du champ magnétique augmente, ce qui induit un champ magnétique induit dans le sens opposé pour lutter contre ce phénomène. Ainsi, la norme I est strictement négative. Pour déterminer la force électromotrice induite E, nous utilisons la loi de Faraday qui indique que E = -(dΦ/dt). En calculant le flux magnétique, on obtient Φ = -πA^3K/Z^3. En dérivant par rapport au temps, on trouve que E = -(3πA^2K)/(V0^3T^4). Pour déterminer la valeur de Z, on utilise la loi des mailles pour établir la relation entre I et E, soit I = E/R. Cela donne I = -(3πA^2K)/(RV0^3T^4). Lorsque l'aimant s'éloigne de la spire, le courant est négatif, ce qui est cohérent avec les résultats obtenus précédemment. L'aspire se comporte comme un aimant avec un moment magnétique dirigé vers le bas suivant l'axe EZ. Par conséquent, elle exerce une force d'attraction sur le véritable aimant. Si l'aimant est immobile mais proche de l'aspire, il n'y a pas de mouvement, donc pas de variation du flux magnétique, et donc pas de courant induit. Cet exercice nous montre comment étudier le comportement d'une spire en tant qu'aimant et prédire ses effets sur le déplacement d'un aimant réel.

Barre et ressort

Aucun résumé n'est disponible pour cette vidéo

Rails de Laplace

Aucun résumé n'est disponible pour cette vidéo

Rail de Laplace + ressort

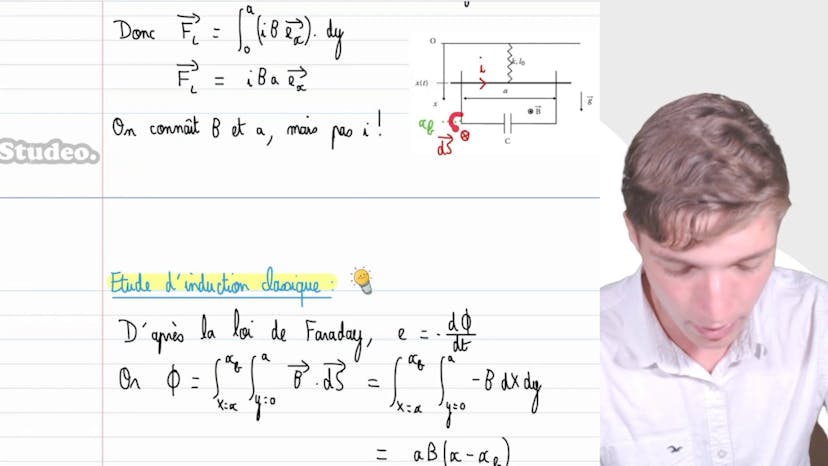
Bonjour à tous, dans cette vidéo nous étudions un dispositif de rails avec une barre attachée à un ressort. La barre a une longueur à vide L0, une constante de raideur k, une masse m, et une longueur a. Lorsque la barre est déplacée de la position d'équilibre x0 à l'instant t = 0, il y a plusieurs phénomènes qui se produisent. Tout d'abord, le ressort va déplacer la barre pour la ramener à sa position d'équilibre. Cependant, en raison du champ magnétique dans lequel se trouve le dispositif, le mouvement de la barre va créer une variation de flux magnétique à travers le circuit, ce qui génère une force de freinage qui ralentit la progression de la barre. De plus, une partie du courant induit va être dissipée par effet joule dans la résistance du circuit. Finalement, le système se stabilisera à la position d'équilibre. Le sens du courant induit dépend du sens du déplacement de la barre. Si la barre se déplace vers la droite, le courant induit va circuler dans le sens opposé. Si la barre se déplace vers la gauche, le courant induit circulera dans le sens de déplacement de la barre. En résolvant les équations électriques et mécaniques du système, nous obtenons l'équation du mouvement x'' + (1/tau)x' + (ω0^2)x = 0, avec tau = MR/AB^2 et ω0^2 = k/m. Pour avoir un régime pseudo-périodique, la résistance R doit satisfaire R < 2AB^2(ω0^2/m)^3. En résolvant cette équation, nous obtenons l'expression de x(t) =