Online Variables aléatoires course by Top Instructors - Variables aléatoires

Binomiale et tirage avec remise

Ce cours explique comment reconnaître et utiliser la loi binomiale. Il commence par définir le schéma de Bernoulli comme une expérience indépendante avec deux résultats possibles (échec ou réussite). Ensuite, il attribue une variable aléatoire x qui suit une loi binomiale de paramètres n et p, où n est le nombre de répétitions et p la probabilité de succès. La probabilité que x soit égal à k est calculée en utilisant la formule 1k parmi n fois p puissance k, 1 moins p puissance n moins k. L'exemple donné est celui de tirer des boules noires sur 8 boules, avec un succès de 3 boules noires sur 5 tirages. En utilisant la formule, la probabilité de réussite est trouvée à 20%. La conclusion est que savoir utiliser la loi binomiale est important pour résoudre des problèmes de probabilité.

Classique : produit défectueux en usine

Le cours traite des produits défectueux en usine et des tests indépendants pour déterminer s'ils sont vendables ou non. La probabilité qu'un produit défectueux soit mis en vente est calculée en utilisant les notations V, T1 et T2. La probabilité de vente est P de T1 inter T2, P de T1 fois P de T2 étant donné que les tests sont indépendants. La probabilité qu'au moins trois produits défectueux soient mis en vente dans une répétition de 100 expériences est calculée en utilisant la loi binomiale. La réussite est définie comme la vente, suivant les notations utilisées dans ce cours. Les calculs donnent une probabilité de 38% de chance de ne pas avoir de produits défectueux en vente, 36% de chance d'avoir un seul produit défectueux et 18% de chance d'avoir deux produits défectueux en vente. La probabilité qu'il y ait plus de trois produits défectueux en vente est de 7%. La formule classique de K par millienne, P à la puissance K, et 1 moins P à la puissance N moins K est utilisée pour les calculs.

Schéma de Bernoulli

Le cours porte sur la reconnaissance et l'utilisation de la loi binomiale. Pour cela, il est nécessaire de suivre deux étapes principales. Tout d'abord, il faut identifier un chemin de Bernoulli, qui est une expérience répétée plusieurs fois de manière indépendante, et qui comporte deux résultats possibles (succès ou échec). Ensuite, il faut attribuer une variable aléatoire x qui représente le nombre de succès. Cette variable suit une loi binomiale avec les paramètres n (nombre de répétitions) et p (probabilité de succès). La formule utilisée pour calculer la probabilité que x soit égal à k est k parmi n fois p à la puissance k, multiplié par 1 moins p à la puissance n moins k. Dans l'exemple donné, il s'agit de tirages successifs et indépendants de boules noires. Le paramètre est de 3 boules noires sur 8 boules, soit une probabilité de réussite de 3 huitièmes. La variable x, qui compte le nombre de boules noires obtenues, suit donc une loi binomiale avec n égal à 5 et p égal à 3 huitièmes. En effectuant les calculs, on trouve une probabilité de 20% pour x égal à 3. C'est ainsi qu'on reconnaît et utilise la loi binomiale. Pour plus d'informations, consultez la FAQ.

Calcul brut de probabilités

Dans ce cours, nous commençons à effectuer les premiers calculs avec la loi binomiale. Pour cela, nous avons besoin d'une calculatrice. La loi binomiale que nous utilisons a un grand X qui suit la loi avec les paramètres n = 50 et p = 0,23. Nous devons calculer trois probabilités. La première probabilité est que p soit strictement inférieur à 12, ce qui est équivalent à la probabilité que x soit inférieur ou égal à 11. Cette donnée peut être obtenue sur toutes les calculatrices graphiques du lycée. En utilisant la calculatrice, nous obtenons un résultat de 0,512. Si nous n'avons pas de calculatrice, il faudrait faire la somme des probabilités de x égale à 1, plus la probabilité de x égale à 2, etc., jusqu'à x égale à 11. Cependant, cela serait fastidieux. C'est pourquoi lorsque nous vous posons cette question, vous avez le droit d'utiliser la calculatrice. Nous aurions également pu vous demander une probabilité sans calculatrice, telle que p de x inférieur à 3. Faire la somme de trois probabilités n'est pas non plus compliqué. Pour la probabilité que x soit supérieur ou égal à 4, je considère plutôt l'événement contraire, qui est l'événement contraire de x inférieur ou égal à 3. Nous pouvons calculer cette probabilité en utilisant 1 moins la probabilité de x inférieur à 3. En utilisant la calculatrice, nous obtenons un résultat de 0,999. Ensuite, nous devons calculer la probabilité que x soit compris entre 5 et 8. Cela revient à calculer la différence entre x inférieur ou égal à 8 et x inférieur ou égal à 5. En utilisant la calculatrice, nous obtenons un résultat. Une autre méthode consiste à considérer que x compris entre 5 et 8 signifie qu'il peut prendre les valeurs 6 ou 7. Nous pouvons donc ajouter les probabilités de x égale à 6 et x égale à 7, ce qui donne un résultat de 0,14. Heureusement, les deux méthodes donnent le même résultat. C'est tout pour les calculs avec la loi binomiale en utilisant la calculatrice. Il suffit de s'assurer que vous connaissez la bonne fonction à utiliser, ce qui est assez facile à trouver. Vous pouvez demander à vos camarades, consulter la FAQ de votre modèle de calculatrice ou chercher sur Google. Les trois méthodes fonctionnent.

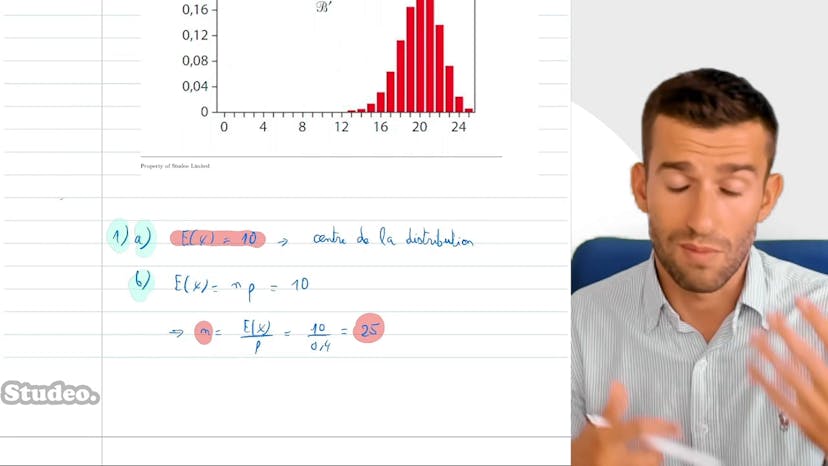
Espérance et écart-type : graphique

Dans ce cours, nous apprenons comment utiliser les diagrammes en barre pour les lois binomiales. Dans le premier exemple, nous avons une loi binomiale avec une probabilité de succès de 0,4, mais nous ne connaissons pas la valeur de N. Nous devons estimer l'espérance. La loi binomiale n'est symétrique que lorsque la probabilité est de 0,5, donc nous estimons que l'espérance est centrée autour de 10. En utilisant la formule de l'espérance (E2x), nous estimons que N est égal à 25. Dans le deuxième exemple, nous devons comparer deux lois binomiales. Nous remarquons que l'une est plus recentrée que l'autre, ce qui signifie que son écart-type est plus faible. L'écart-type mesure l'écart à la moyenne, et plus il est élevé, plus les valeurs sont loin de l'espérance. Les valeurs importantes à retenir sont l'espérance (NxP), la variance (NPx-P), et l'écart-type (racine carrée de la variance). Enfin, dans un exercice supplémentaire, nous cherchons à déterminer quelle valeur de P est la plus faible. En utilisant la fonction f2x égale à x fois 1-x, nous trouvons que l'écart-type maximum est atteint lorsque la probabilité vaut 1,5. Cela est dû au fait qu'il y a autant de chances d'échec que de réussite, ce qui peut entraîner des résultats très différents. En résumé, ce cours explique comment utiliser les diagrammes en barre pour les lois binomiales, estimer l'espérance et comparer différentes lois binomiales en fonction de leur écart-type.

Déterminer le + grand entier

Dans cette vidéo, Corentin aborde un exercice sur les variables aléatoires suivant des lois binomiales. L'énoncé demande de trouver le plus grand entier k tel que la probabilité que X soit supérieur ou égal à k soit supérieur ou égal à 0,9. Pour résoudre cet exercice, Corentin observe que la probabilité diminue lorsque k augmente car l'ensemble X supérieur ou égal à k devient de plus en plus petit. Son approche consiste donc à chercher le cas où la probabilité que X soit supérieur ou égal à k+1 est strictement inférieure à 0,9 et la probabilité que X soit supérieur ou égal à k est supérieur ou égal à 0,9. En utilisant sa calculatrice, Corentin trouve que la probabilité que X soit supérieur ou égal à 22 est égal à 0,80, celle de 21 est égal à 0,89 et celle de 20 est égal à 0,95. Il en conclut que le plus grand entier k qui satisfait les conditions est 20.