All subjects
- All subjects
Schéma de Bernoulli
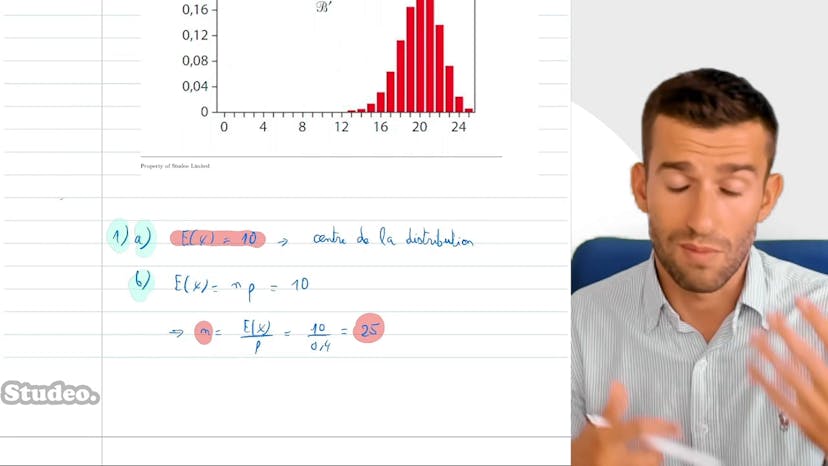
La vidéo traite de la reconnaissance et de l'utilisation de la loi binomiale en statistiques. Pour cela, il faut identifier un chemin de Bernoulli, qui consiste en la répétition indépendante d'une même expérience avec deux issues possibles : échec ou réussite. Ensuite, on attribue une variable aléatoire x qui compte le nombre de succès, et cette variable suit une loi binomiale de paramètres n (nombre de répétitions) et p (probabilité de succès). La formule utilisée pour calculer la probabilité que x soit égal à k est k parmi n multiplié par p élevé à la puissance k, multiplié par 1 moins p élevé à la puissance n moins k. Dans l'exemple donné, il s'agit de tirages successifs et indépendants pour lesquels le succès est de tirer une boule noire parmi 3 boules noires sur un total de 8 boules (soit une probabilité de 3/8). Ainsi, la variable x qui compte le nombre de boules noires obtenues suit une loi binomiale de paramètres n égal à 5 et p égal à 3/8. En effectuant les calculs, on obtient une probabilité de 20% que x soit égal à 3. Pour plus d'informations, consultez la FAQ.
