Home

2BAC SM Maroc

Maths SM&SP

Analyse

Dérivée seconde et convexité

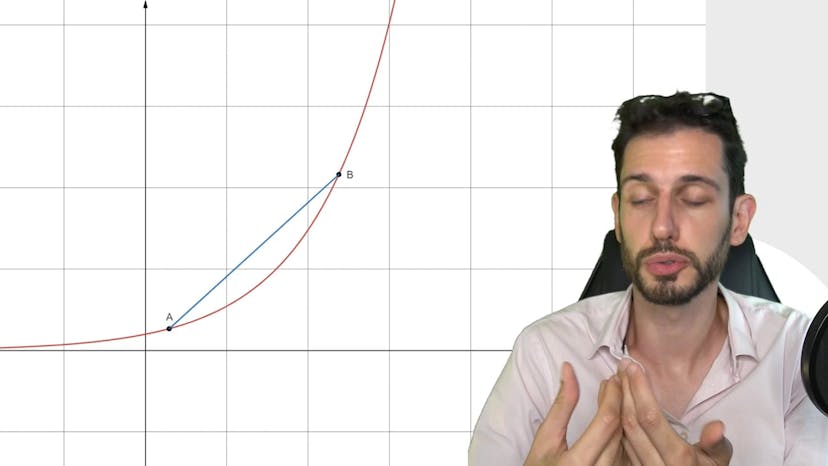
Dans ce cours, nous abordons la convexité d'une fonction dérivable. Nous rappelons que la convexité ne dépend ni de la continuité, ni de la dérivabilité de la fonction, mais seulement de la position entre les séquentes et la courbe de la fonction.

Nous simplifions la définition pour la rendre plus pratique pour une utilisation quotidienne. Nous expliquons que f est convexe sur un intervalle i si, pour tout réel x de cet intervalle, f' est croissante. De même, f est concave sur i si f' est décroissante.

Nous illustrons cela avec l'exemple de la fonction cubique. Nous observons que la fonction est concave au début et convex à la fin. Nous expliquons que cela correspond à la décroissance de la dérivée f', puis à son augmentation.

Nous utilisons également la dérivée seconde pour étudier la convexité. Nous expliquons que si f est deux fois dérivable et que f' est positive, alors f est convexe. Ainsi, plutôt que de comparer les courbes et les droites, il suffit de calculer la dérivée seconde f'' pour déterminer la convexité.

En conclusion, il est plus pratique d'étudier la convexité d'une fonction dérivable en calculant sa dérivée seconde. Cela simplifie l'étude en réduisant l'analyse à un simple calcul de dérivée.

Un aspect très important de la convexité, c'est quand on a une fonction qui est dérivable. On a vu que la convexité, c'était quelque chose qui ne dépendait pas ni de la continuité, ni de la dérivabilité de la fonction, mais uniquement de la position entre la séquente et la courbe de la fonction, les séquentes et la courbe de la fonction. Maintenant, on va s'intéresser à la convexité dans un cas où f' va être dérivable et f' va exister. Donc ça va être intéressant. Si on a une fonction qui est dérivable, on pourra peut-être avoir d'autres approches, d'autres définitions de la convexité qui sont peut-être plus pratiques au jour le jour, si vous voulez. Quand vous faites un exo, on n'est pas obligé de revenir à la démonstration de la définition pure et la comparaison à la séquente. Ça va être plus pratique. Si vous voulez, on est dans un cas très général, on va un peu simplifier. On va partir de la grosse généralité et simplifier un peu pour se raccorder quand même aux fonctions qu'on rencontre le plus souvent en terminale. Donc f va être convex sur un intervalle i, si et seulement si, pour tout réel x de cet intervalle, f' est croissante. De la même manière, f est concave sur i, si et seulement si, f' est décroissante. Illustration tout de suite, parce que sinon on ne va pas comprendre. Voici une fonction cube. Si on regarde cette fonction, qu'est-ce qui a l'air de se passer sur cette fonction ? J'ai l'impression que pour un certain comportement de départ, cette fonction est concave. J'ai l'impression qu'elle est concave au départ. Donc par exemple, si je trace un petit point, laissez-moi faire ça. Voilà. Si je trace un petit point comme ça, j'ai l'impression que toute cette zone ici, ma fonction est concave. Elle fait la tronche. Je sais que c'est un peu nul comme définition, mais moi ça marche. Concave, c'est quand ça fait la tête, le sourire en debas. Ça a l'air d'être concave au début, puis à partir de là, ça commence à changer. Et là en tout cas, j'ai un truc qui est convex. Donc j'ai une partie convexe ici, une partie concave ici, donc c'est un bon exemple pour voir un peu ce qu'il se passe. On a dit que la fonction va être concave quand la dérivée va être décroissante. Ça a l'air vrai. Honnêtement, si je trace par exemple, si je regarde vite fait là, le coefficient directeur de la tangente au point, à l'endroit où j'ai mon point là, il a l'air très élevé. Donc j'ai un coefficient directeur très fort, du genre 8 ou 9. Plus j'avance vers là, plus le coefficient directeur a l'air de diminuer. Mais la valeur du coefficient directeur, c'est la valeur de la dérivée. Donc ça veut dire que la valeur de f' a l'air de diminuer. On passe de f' égale, je ne sais pas, à 9, 5, 4, 3, 0, moins 1, moins 2 peut-être. Moins 1, je ne sais pas. Donc on a bien une fonction f' qui a décroît. Qui a cru, qui a décru. Peut-être qu'il y a décru. On a bien une fonction en gros f' qui diminue. Et ensuite là, qu'est-ce qu'il se passe ? Imagine donc là, j'ai ma pente qui vaut genre moins 1. Mais qu'est-ce qu'il se passe à partir de maintenant, le point exact où je suis ? On passe de moins 1 à moins 0, 5, à 0, 1, 2, 3, 4 et ça réaugmente. Et donc on a une augmentation de f', une fonction f' croissante au moment où c'est convex. C'est bien un parallèle entre les deux. Ce sera encore plus facile si je vous le montre avec ça en fait. Donc ça par exemple, c'est ma fonction dérivée. Ma fonction dérivée, c'est une parabole parce que ma fonction, je vous ai dit, c'est un x3. Donc voilà, ma fonction dérivée, c'est une fonction x². Regardons un peu, j'ai dit, ma fonction noire sera concave quand f' est décroissant. Et j'ai dit que c'était à peu près jusqu'à ici. Mais en effet, si vous suivez la courbe bleue en même temps, c'est vrai que là, c'est la zone où la courbe bleue est en train d'être décroissante. Et dès que la courbe bleue commence, qui est donc ma dérivée, commence à recroître, hop, je suis convex. Une autre manière de le voir, ce serait aussi de tracer cette chose-là, hop, la tangente. Si je trace ma tangente comme ça au fur et à mesure, je vois que ma tangente est, alors je peux virer ça sans avoir un peu de clarté, hop, ça, je cache aussi, on va partir sur ça plutôt. Donc j'ai une tangente qui est très très très positive, elle diminue, diminue, diminue, diminue, diminue. Pendant tout ce moment où je suis concave, c'est la diminution de la pente qui me rend concave si vous voulez. Puis à partir de là, ça va commencer à réaugmenter et c'est là que je suis convex. Voilà, c'est mon illustration, c'est un peu long mais je pense que vous avez compris l'idée avec le dessin. Et donc c'est pour ça qu'on a cette propriété, je voulais l'illustrer, j'espère que c'est clair maintenant. Voyons maintenant ce qui se passe pour une dérivée seconde potentielle. Déjà définition, qu'est-ce qu'une dérivée seconde ? Une dérivée seconde, c'est quand on peut redériver f. Imaginons qu'on dérive f, ça donne f'. Si f' elle-même est une fonction dérivable, par exemple si j'avais f qui est x³, f' devient 3x², 3x² ça se dérive donc je peux faire une double dérivée, on appellera ça f''. J'ai mis quelques exemples, par exemple vous avez x3 plus 4x² plus 5x plus 1, je la dérive une fois, ça fait 3x² plus 4 x2x plus 5, je dérive chacun des morceaux un par un. Ok, très bien, mais y'a pas de raison que ce 3x² plus 8x plus 5 je ne puisse pas le redériver, et dans ce cas ça s'appelle f''. On redérive, donc deuxième prime ça fait 6x plus 8. Bon. On a parlé de décroissance et de croissance de f', dans le slide précédent. Si vous vous souvenez c'est ça. Peut-être que je peux étudier f' lors que sa croissance et décroissance grâce à la dérivée de f'. Quand on veut savoir si une fonction est croissante ou décroissante, on étudie sa dérivée. Donc croissance de f', je vais la dériver. Et donc je vais pouvoir dire... Petite remarque que j'ai un peu zappée. La dérivée seconde d'une fonction affine est toujours nulle, ça vous pouvez le calculer vite. Ax plus b, vous dérivez une fois, il reste a, deuxième fois, il reste 0. Exponentielle, vous pouvez la dériver autant de fois que vous voulez, ça va toujours être égal à elle-même. Ça c'était une remarque. Et donc, je disais, si f est deux fois dérivable et qu'on a f' sa dérivée, comme on a dit que f était convexe, disons, si et seulement si, c'était convexe, si et seulement si, f' était croissante. Ça veut dire qu'on va être convexe, si et seulement si, la dérivée de f' est positive. Donc on aura f' convexe, si et seulement si, f' prime positive. Et donc là, votre vie est vachement améliorée. Parce qu'au lieu de vous embêter à comparer la courbe, les droites, les machins, super chiant, vous pouvez juste calculer une double dérivée. Ce qui est assez rapide, notamment dans les 4 fonctions polynomiales ou exponentielles. Parce que la définition précédente était un peu moins générale que celle des séquentes, mais elle disait juste qu'il faut étudier les variations de f'. Et bien, étudier les variations, comment on fait ? Si on a la chance que f' elle-même soit dérivable, ce qui sera le cas dans 99% des cas, alors il suffit donc d'étudier f''. Et donc votre étude de la convexité se réduit maintenant à un double calcul de dérivée. f' on calcule, quand c'est positif, sur les zones où f' est positive, la courbe sera convexe, sur les zones où f' est négative, la fonction sera concave. Parce que la fonction n'est pas toujours uniquement concave ou convexe, comme on a vu dans la fonction x3 qui était comme ça. Et donc c'est assez simple. La démonstration, c'est lié au théorème d'avant sur le fait que f' est convexe quand f' est croissante. C'est tout ce que j'avais à dire là-dessus. J'espère que c'était assez clair. Posez des questions dans le forum, bien sûr, si ce n'est pas toujours clair. Et je vous dis à la prochaine, pour une prochaine vidéo.

Lien dérivation

RELATED

Recommended videos

Intuition et déf

Fonctions usuelles

Inégalité fondamentale