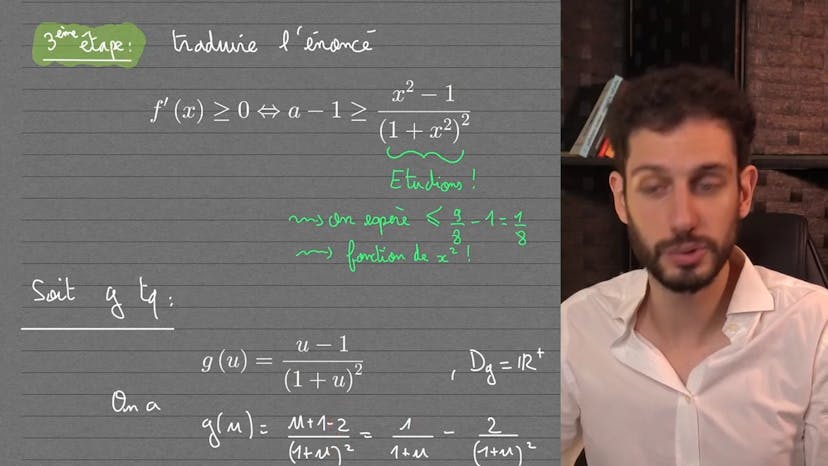All subjects
- All subjects
Dériver 1, 2, ... 3 fois !!
Dans cet exercice, nous étudions une fonction complexe, F2x, ainsi que d'autres fonctions F, G et H qui augmentent en difficulté. Nous devons démontrer différentes propriétés de ces fonctions, telles que leur positivité sur certains intervalles.
Tout d'abord, nous examinons la fonction F et remarquons qu'elle est strictement croissante sur l'intervalle [0, +∞), car sa dérivée est positive ou nulle. En utilisant cette propriété, nous montrons que F2x est positif ou nul pour tout x positif, ce qui répond à la première question.
Ensuite, nous passons à la fonction G et effectuons des calculs similaires pour montrer qu'elle est également positive sur l'intervalle [0, π/2). En dérivant deux fois, nous prouvons que la dérivée seconde de G est positive sur cet intervalle, ce qui implique que la dérivée première de G est croissante et que G est positive.
Nous répétons cette procédure pour la fonction H et démontrons qu'elle est positive sur l'intervalle [0, π/4). En dérivant plusieurs fois, nous constatons que la dérivée troisième de H est positive, ce qui entraîne une croissance stricte de la dérivée seconde de H et donc une positivité de H.
Enfin,
