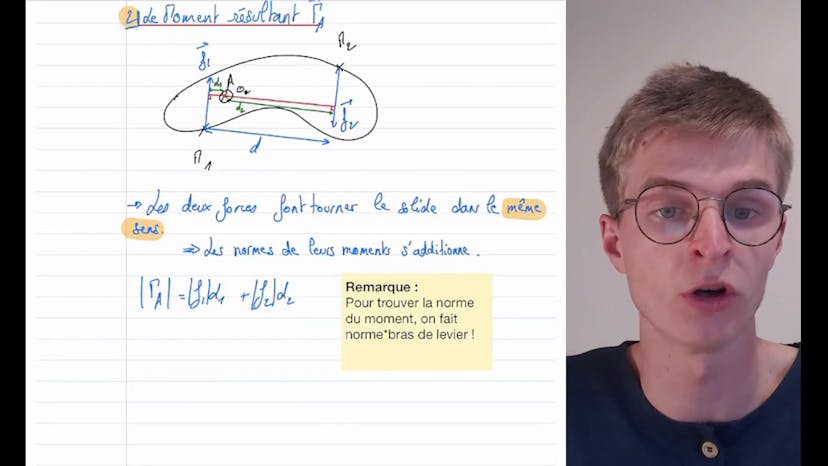
All subjects
All subjects
 All subjects
All subjects
Moment cinétique d'un point de masse M
Dans cette vidéo, nous étudions le moment cinétique d'un point M se déplaçant en trajectoire circulaire autour d'un point O. Le point M possède une masse M et se déplace selon des coordonnées cylindriques. Le but de l'exercice est de calculer le moment cinétique Lz par rapport à l'axe OZ.
Pour cela, nous commençons par faire un schéma de la situation, en représentant les vecteurs Uz, Ur et Uteta. Le point M se trouve à une distance R du centre O. Le moment cinétique d'un point M est le produit vectoriel de son vecteur position OM et de son vecteur vitesse MV. En substituant les valeurs, nous obtenons L = MR²θ.Uz.
Cependant, nous cherchons le moment cinétique par rapport à l'axe OZ. En observant le schéma, nous remarquons que Uz et L sont tous les deux parallèles à OZ. Cela signifie que toutes les composantes du moment cinétique sont alignées avec OZ. Par conséquent, le produit scalaire entre L et Uz est égal à la norme de L.
Ainsi, le moment cinétique par rapport à l'axe OZ du point M est égal à MR²θ.Uz. Ce résumé permet de poser les bases avant de passer à la suite du cours. Si vous avez des questions, n'hésitez pas à les poser. Merci.