Home

MPSI/PCSI

Corrigés de BAC

Bac Physique-Chimie

Nouvelle Calédonie 1

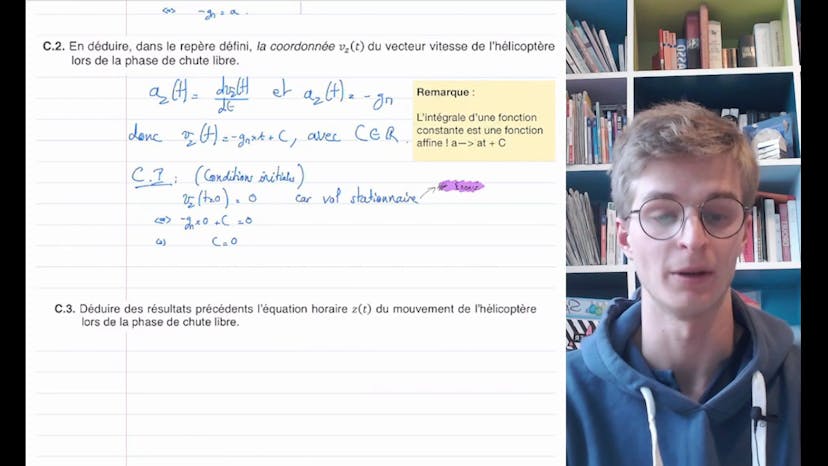
Dans cette vidéo, le professeur Théobald de Studio présente une résolution d'un problème ouvert en physique chimie, qui consiste à déterminer la valeur de la vitesse de rotation minimale des pales de l'hélicoptère Ingenuity sur Terre et sur Mars, afin que l'hélicoptère puisse décoller. Pour résoudre ce problème, le professeur propose une démarche en plusieurs étapes.

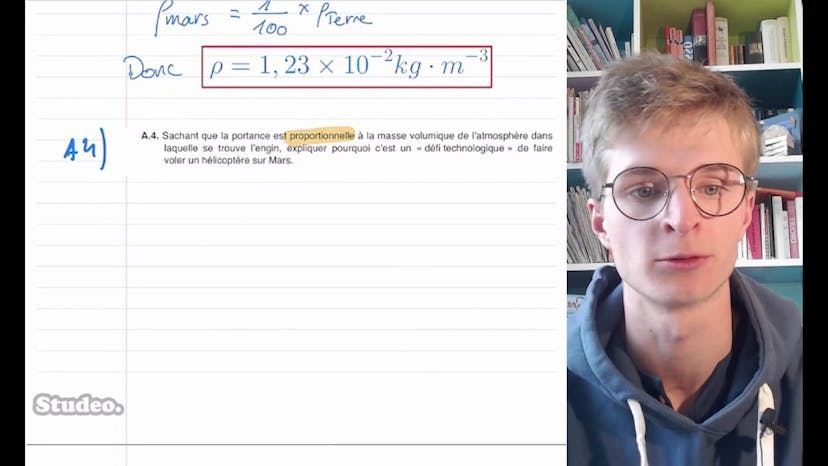
Tout d'abord, il explique que la portance minimale nécessaire à l'hélicoptère pour décoller doit compenser le poids de l'appareil. Il souligne que la portance et le poids sont deux forces, et que la portance minimale correspondra donc au poids de l'hélicoptère. Sachant que le poids dépend de l'intensité de pesanteur sur Terre et sur Mars, il faut d'abord trouver le poids de l'hélicoptère sur chaque planète.

Ensuite, le professeur utilise des graphiques représentant la portance en fonction de la vitesse de rotation des pales sur Terre et sur Mars. Il explique que chaque valeur de portance correspond à une vitesse de rotation des pales spécifique. Donc, pour trouver la vitesse de rotation minimale correspondant à la portance minimale, il faut utiliser ces graphiques.

Le professeur procède ensuite au calcul du poids de l'hélicoptère sur Terre et sur Mars, en utilisant les valeurs de masse de l'hélicoptère et les intensités de pesanteur fournies dans l'énoncé. Il obtient ainsi les valeurs de portance minimale sur Terre et sur Mars.

Enfin, le professeur lit les valeurs de vitesse de rotation minimales correspondantes sur les graphiques, en utilisant la règle pour lire les données. Il obtient ainsi les valeurs de vitesse de rotation minimales sur Terre et sur Mars.

Le professeur commente ensuite le résultat, en soulignant que la vitesse minimale de rotation sur Mars est 6 fois plus élevée que sur Terre. Il explique que cela met en évidence le défi technologique que représente le vol de l'hélicoptère sur Mars.

En conclusion, le professeur souligne l'importance d'essayer de résoudre le problème même si on n'obtient pas nécessairement un résultat final. Il rappelle que le cheminement et la démarche de résolution sont également évalués dans ce type de questions.

Bonjour à tous, c'est Théobald de Studio, et dans cette vidéo, on va corriger ensemble la partie B de l'exercice 1 du bac de Nouvelle-Calédonie de 2022 en physique chimie. C'est toujours de la physique, et on va s'intéresser au décollage de l'hélicoptère. Et donc, ça va être un problème ouvert. Et donc, tout de suite, on va résoudre ensemble ce problème ouvert. Alors, vu que c'est un problème, on va aller voir la question qui est, je vous la lis, déterminer la valeur de la vitesse de rotation minimale des pales d'Ingenuity sur Terre et sur Mars, donc on attend deux valeurs, afin que l'hélicoptère décolle. On nous dit de commenter le résultat. On nous dit aussi que le candidat est invité à prendre l'initiative... Ça, ça veut dire que c'est un problème ouvert. Ça va être à vous d'arriver jusqu'au résultat, selon la méthode de votre choix. Et c'est cette méthode, cette démarche qui va être évaluée au même titre que votre résultat final. Alors, on va essayer d'établir un peu une démarche ensemble. On relit le début, on nous dit, pour pouvoir décoller, ça nous intéresse, vu qu'on veut la portance minimale, donc la vitesse de rotation des pales minimale pour pouvoir décoller, on nous dit que la portance doit au moins compenser le poids de l'hélicoptère. La portance qui est une force doit compenser le poids qui est aussi une force. C'est cohérent jusque là. Et donc, si on nous dit que ça doit au moins compenser le poids de l'hélicoptère, ça veut dire que la portance minimale, ça va être celle qui est égale au poids de l'hélicoptère. Le poids de cet hélicoptère va dépendre de si on est sur Mars ou sur Terre, vu que les intensités de pesanteur sont différentes sur les deux planètes. Une fois qu'on aura la portance, parce que, du coup, première étape, trouver le poids de l'hélicoptère sur Mars et sur Terre, deuxième étape, trouver la portance minimale, donc qui est égale au poids sur Mars et sur Terre, et une fois qu'on a ça, en fait, on utilisera ces petits graphes qui sont la portance en fonction de la vitesse de rotation des pâles sur Terre et sur Mars. Et donc, à une portance donnée, correspond une vitesse de rotation des pâles donnée. Donc, on va faire ça ensemble. Première étape, trouver le poids de l'hélicoptère. Alors, on nous dit d'après l'énoncé que la masse de l'hélicoptère, c'est 1,8 kg, et l'énoncé nous donne aussi les intensités de pesanteur sur Terre et sur Mars. Sur Terre, c'est 9,8 mètres par seconde moins 2, et sur Mars, c'est 3,7 mètres par seconde moins 2. Et à partir de là, on va pouvoir calculer les poids de l'hélicoptère sur Mars et sur Terre, en faisant bien attention aux chiffres significatifs. Donc, sur Terre, on a notre poids qui vaut 17 N, et sur Mars, il vaut 6,7 N. À partir de là, on va trouver la portance minimale. La portance minimale, on nous dit d'après l'énoncé que l'hélicoptère va décoller si la portance est supérieure ou égale au poids. Donc, la plus petite, c'est celle qui est égale au poids. Donc ça, ça veut aussi dire que, si on retraduit ça, c'est-à-dire que la norme de la portance doit être supérieure ou égale à la norme du poids. On parle ici en normes, en fait. Donc, les deux normes doivent être égales pour avoir la portance la plus petite possible pour que l'hélicoptère décolle. Et donc, on peut tout de suite trouver les portances. Fpt mine, donc ça, c'est la force de portance sur Terre minimale, qui vaut 17 N. Et Fpm mine, force de portance sur Mars minimale, qui vaut 6,7 N. L'étape suivante, c'est de se dire quelle est la vitesse de rotation correspondante à cette portance. À quelle vitesse est-ce que je vais faire tourner mes pales pour avoir cette force de portance ? Pour ça, on va utiliser la règle pour lire les données sur les graphiques. Alors, on remonte. Et puis, pour la Terre, je ne sais pas si on voit bien l'écran, mais je vais essayer de le refaire. On place à 17 N. Quand on croise la courbe, on redescend pour connaître notre vitesse de rotation pour obtenir ces 17 N. Et donc, on trouve quelque chose de l'ordre de 380 tours par minute. On fait pareil sur Mars. Sur Mars, on était à 6,7 N comme force de portance minimale, correspondant à une vitesse de rotation de l'ordre de 2480 tours par minute. Et donc, on écrit juste sur notre copie, on lit sur le graphe. Ici, le nombre de tours par minute sur la Terre qui vaut 380 tours par minute. Et sur Mars, 2420 tours par minute. Donc, on a bien trouvé nos vitesses de rotation minimales. On a répondu à la question. On nous demande aussi de commenter le résultat. Pour commenter le résultat, je dis que sur Mars, la vitesse minimale de rotation est 6 fois plus élevée que sur Terre. En fait, c'est assez intéressant de commenter nos résultats avec des rapports de grandeur. Ça parle assez bien de dire qu'il faut que les pales tournent 6 fois plus vite que sur Terre si on est sur Mars. On comprend bien le défi technologique qui est derrière. Et donc, juste petit rappel, sur ce genre de questions, il faut essayer d'en faire le plus possible. Même si vous n'avez pas un résultat à la fin, si vous écrivez déjà uniquement ce que j'ai surligné en jaune, c'est déjà bien. Vous avez compris le cheminement. Ça va quand même vous rapporter des points, même si vous n'allez pas jusqu'au bout des calculs. J'espère que ça a été clair. Si vous avez des questions encore, n'hésitez pas à les poser en commentaire. Et puis, à la prochaine pour la suite de cet exercice.

Ingenuity : le premier hélicoptère à voler sur Mars (2)

RELATED

Recommended videos

Ingenuity : le premier hélicoptère à voler sur Mars (1)

Ingenuity : le premier hélicoptère à voler sur Mars (3)