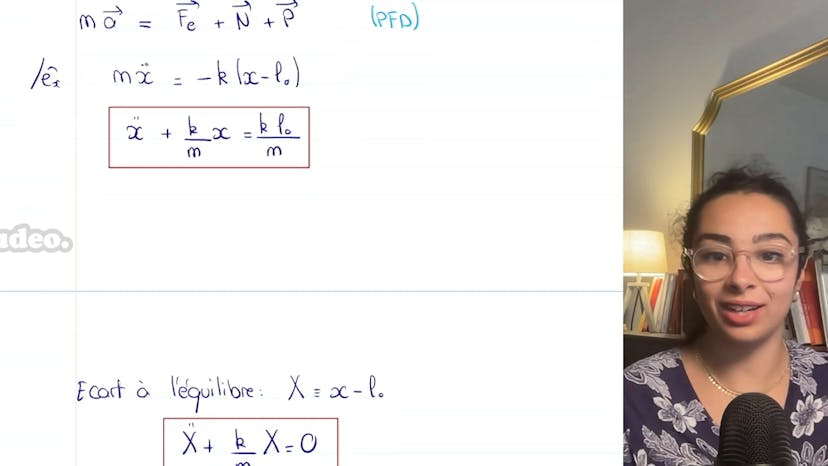Home

MPSI/PCSI

Physique-Chimie

Physique

Mécanique vibratoire

Dans cette vidéo, nous poursuivons notre série en résolvant l'équation différentielle d'un oscillateur harmonique. Nous examinons spécifiquement l'équation d'oscillateur harmonique que nous avons abordée dans la vidéo précédente pour le système de masse ressort, mais qui est également applicable à de nombreux autres types de systèmes. 

Dans cette équation, x représente l'écart par rapport à l'équilibre. Pour bien comprendre d'où cela vient, nous adoptons une approche mathématique et vous verrez ensuite qu'il existe des raccourcis en physique. L'équation caractéristique de cette équation différentielle est r² + ω0² = 0, ce qui donne les solutions r = ±iω0. En combinant les exponentielles de chacune de ces solutions, nous obtenons AEiω0t + BE-iω0t.

Cependant, en physique, nous nous intéressons uniquement aux nombres réels. Ainsi, si nous exprimons ces solutions en réel, nous obtenons une forme λcosω0t + μsinω0t. Une autre façon pratique de l'écrire est de prendre x0 au lieu de λ, ce qui nous donne une expression de la forme x0cosω0t. Vous pouvez choisir la méthode qui vous convient le mieux. Personnellement, j'aime les combinaisons linéaires de cosinus et de sinus, car je m'y suis habitué et je trouve que cela fonctionne bien. Cependant, le déphasage peut parfois être plus pratique.

Si nous n'avons pas de vitesse initiale, x.0 = 0 et x(0) = x0. Dans ce cas, la constante λ est égale à x0 et la constante μ est égale à 0. Cela nous donne donc xt = x0cosω0t. Si nous considérons exactement le même type d'expression avec φ = 0, nous pouvons utiliser la même méthode pour les conditions initiales.

On continue cette série de vidéos avec la résolution de l'équation différentielle d'un oscillateur harmonique. Donc ici tout simplement on va faire la résolution de l'équation d'oscillateur harmonique qu'on a vu dans la précédente vidéo pour le système masse ressort, mais que vous retrouvez aussi dans plein de types de systèmes. Donc ici x je vous rappelle que c'est l'écart à l'équilibre et donc pour ça je vous propose une approche vraiment mathématique des choses pour bien comprendre d'où ça vient, et ensuite vous verrez que vous pourrez utiliser des petits raccourcis en physique. Donc l'équation caractéristique de cette équation différentielle c'est r² plus ω0² est égal à 0, donc les solutions sont r est égal à plus ou moins iω0, et donc vous savez que vous combinez en fait les exponentielles de chacune des solutions, donc ça vous fait AEiω0t plus BE-iω0t. Ici on est en physique, ce qui nous intéresse c'est uniquement les réels et donc ça, si je le passe en réel, ça me donne quelque chose de la forme λcosω0t plus μsinω0t. Une autre manière de l'écrire qui est parfois pratique c'est de dire que x0, de mettre en fait au lieu d'avoir une combinaison un sinus et un cosinus, de passer l'un des deux sous la forme d'un déphasage qui nous donne une expression de la forme x0cosω0t. C'est à vous de choisir la méthode que vous préférez, moi personnellement j'aime bien les combinaisons linéaires de cosinus et sinus, je me suis un peu habituée avec et je trouve que ça marche bien, mais c'est pas la seule option et parfois le déphasage est plus pratique. Si on n'a pas de vitesse initiale, on a x.0 qui est égal à 0, x en 0 qui est égal à x0, donc la constante λ est égale à x0 et la constante μ est égale à 0, ça nous donne xt qui est égal à x0cosω0t. Vu qu'on retrouve exactement ce même type d'écriture avec φ égal à 0, on pourrait s'amuser à faire de la même manière les conditions initiales.

Oscillateur harmonique

RELATED

Recommended videos

Masse-ressort

Pendule simple