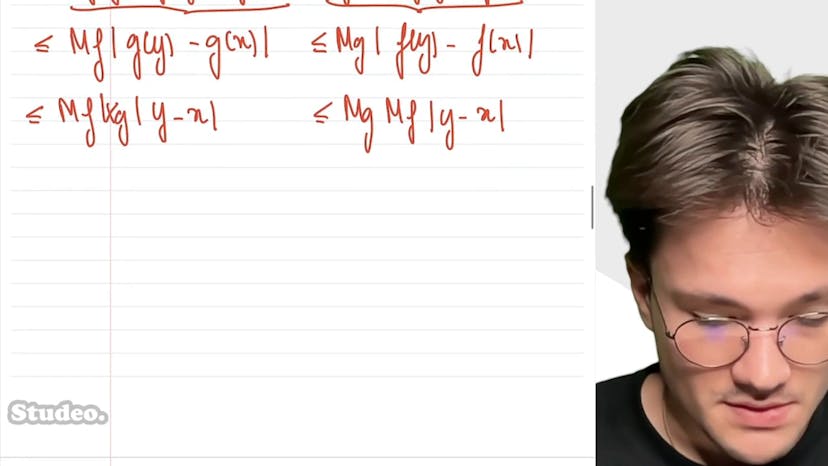Home

MPSI/PCSI

Maths

Analyse

Fonctions (1) : Sujets d'écrits

Dans ce cours, Corentin parle de la Lipschitzianité et de l'uniformité de continuité des fonctions. Il commence par montrer que si une fonction est Lipschitzienne et qu'un réel alpha est ajouté à son argument, alors la nouvelle fonction obtenue est aussi Lipschitzienne. Ensuite, il montre que la fonction sinus est Lipschitzienne et que sa fonction dérivée, le cosinus, est également Lipschitzienne. Finalement, il explique ce qu'est une application uniformément continue et montre que si une fonction est Lipschitzienne, alors elle est également uniformément continue. Il prouve ensuite que la réciproque, à savoir qu'une fonction uniformément continue n'est pas forcément Lipschitzienne, est fausse. Il illustre cela par un exemple de fonction uniformément continue mais non Lipschitzienne, la fonction valeur absolue de x à la racine.

Rebonjour à tous, c'est Corentin. On se retrouve pour la troisième partie de la correction de notre sujet d'écrit, avec cette fois-ci les questions 6, 7 et 8. Alors commençons tout de suite par la question 6. Soit f une fonction Lipschitzienne et α un réel? Et on veut montrer que l'application qui a x associé f de x plus α est-elle aussi Lipschitzienne? Alors commençons tout de suite. Moi ce que j'ai choisi de faire c'est de montrer que T indice α est un Lipschitzienne. Pourquoi? Soit x et y deux réels. Je remarque que T indice α de y moins T indice α de x c'est égal à y plus α moins x moins α. C'est égal à y moins x. Conclusion, T indice α est un Lipschitzienne. Vous avez vu c'est assez simple. Or d'après la question A2, on sait que la composée de deux fonctions Lipschitziennes c'est elle aussi une fonction Lipschitzienne. Et moi je remarque quoi? Que la fonction qui a x associé f de x plus α c'est la composée de T indice α par f. On en conclut donc que f rond T indice α qui est la fonction qu'on nous donne dans l'énoncé est K indice f Lipschitzienne. Passons maintenant à la question 7. La question 7 qui nous demande de montrer que la fonction sinus est Lipschitzienne et d'en déduire que la fonction cosinus est elle aussi Lipschitzienne. Et ce que fait l'énoncé, mais que je vais vous illustrer un peu, c'est un rappel qui nous dit que pour toute x dans R+, la valeur absolue de sinus de x est inférieure ou égale à x. Pourquoi? Parce que si je trace la droite y qui est égale à x, je remarque clairement qu'elle est supérieure ou égale à sinus de x pour toute x dans R+. Mais en fait c'est la même chose dans R- si on passe tout à la valeur absolue. On peut imaginer que ça va être comme ça. Voilà, c'est ce que nous donne l'énoncé. On va s'en servir, vous allez voir comment. Soit donc x et y de Réel. Et là je suppose que x est strictement inférieur à y, mais ça ne réduit en rien la généralité de la preuve. La valeur absolue de sinus de y moins sinus de x, je le transforme, avec une formule qui est donnée dans l'énoncé mais que je vous conseille de connaître, en 2 fois sinus de y moins x sur 2 fois cosinus de y plus x sur 2. Ça, je le majeure maintenant. Je le majeure en utilisant le rappel ici et en sachant que cosinus, c'est borné par 1. Je mène à bien mes calculs et je trouve finalement que sinus de y moins sinus de x est inférieur ou égal à y moins x. Conclusion, la fonction sinus est bien un Lipschitzienne. Pour ce qui est de la fonction cosinus, ce que je remarque c'est que cosinus de x est égal à sinus de x plus pi sur 2. Ça, c'est à connaître par cœur, on est censé savoir depuis le lycée. Mais bon, si vous ne vous en souvenez pas trop, ce n'est pas grave, je ne vous en veux pas trop. De là, sachant que la fonction qui a x associée au sinus de x est Lipschitzienne, et en appliquant la question A6, on en déduit que cosinus est également un Lipschitzienne. Passons à présent à la question A8, qui nous demande de montrer que toute application Lipschitzienne est uniformément continue, mais de montrer aussi que la réciproque est fausse, c'est-à-dire que ce n'est pas parce qu'une fonction est uniformément continue qu'elle est Lipschitzienne. Alors il va falloir trouver un petit contre-exemple. Et puis moi, ce que je vous propose de faire à ce stade, c'est un petit rappel sur ce qu'est une application uniformément continue. On dit qu'une fonction qui va de i dans R avec i en ouvert de R est uniformément continue si et seulement si pour tout ε strictement supérieur à 0, il existe un δ strictement supérieur à 0, tel que pour tout x et y dans i², le fait que la distance de x à y soit inférieure à δ implique que la distance de f de x à f de y soit inférieure à ε. Soit donc f une application Kalipschitzienne, soit ε strictement supérieur à 0. C'est comme ça qu'on débute toutes les preuves pour montrer continuité, limite, uniforme continuité. On fixe ε et puis on voit après. Moi ce que je vous propose de faire, c'est de poser δ est égal à ε sur k. Pourquoi? Parce que de là, soit x et y dans R², vérifiant, la distance de x à y est strictement inférieure à δ. On a alors f de x moins f de y est strictement inférieure à k fois x moins y, parce que f est Lipschitzienne. Sauf que, on sait que x moins y sont à une distance inférieure à δ, donc on peut encore majorer. Et puisqu'on a pris δ est égal à ε sur k, on trouve que f de x moins f de y est inférieur à ε. Conclusion, f est bien uniformément continu, montrant à présent que la réciproque est fausse. Et ce que je vous propose de faire, c'est d'exhiber un exemple d'application uniformément continue, mais non Lipschitzienne sur R. Et l'exemple classique, c'est la fonction qui a x associé valeur absolue de x à la racine. Supposons par l'absurde que la fonction qui a x associé valeur absolue de x à la racine est Lipschitzienne. Alors, pour toute y dans R, valeur absolue de y à la racine moins valeur absolue de 0 à la racine est inférieure ou égale à k fois y moins 0. Mais alors, en posant y est égal à 1 sur n, on remarque que 1 sur racine de n est inférieur ou égal à k fois 1 sur n. En passant ce n de ce côté-là, on trouverait alors que racine de n est inférieure ou égal à k. Et c'est un peu la même mécanique que tout à l'heure, c'est-à-dire que j'ai exhibé une suite qui tend vers plus l'infini mais qui se rébornait. Et ça c'est complètement absurde. En conclusion, cette fonction-là n'est pas Lipschitzienne et pourtant elle est uniformément continue.

Type Mines : Partie A - 3/4

RELATED

Recommended videos

Type Mines : Partie A - 1/4

Type Mines : Partie A - 2/4