 Tous les sujets
Tous les sujets Maths
Maths- Nombres et calculs
- Géométrie
- Fonctions
- Stats et Probas
- Analyse
- Géométrie
- Probas et Stats
- Analyse (spé)
- Géométrie (spé)
- Probabilités (spé)
- Arithmétique (exp)
- Complexes (exp)
- Analyse
- Algèbre
- Analyse
- Algèbre
- Probabilités
SecondePremièreTerminale2BAC SM MarocMPSI/PCSI Physique-Chimie
Physique-Chimie Corrigés de BAC
Corrigés de BAC Révisions Maths lycée
Révisions Maths lycée Prépa Examens
Prépa Examens
Terminale
Première
Seconde
MPSI/PCSI
2BAC SM Maroc
 Tous les sujets
Tous les sujets Maths
Maths- Nombres et calculs
- Géométrie
- Fonctions
- Stats et Probas
- Analyse
- Géométrie
- Probas et Stats
- Analyse (spé)
- Géométrie (spé)
- Probabilités (spé)
- Arithmétique (exp)
- Complexes (exp)
- Analyse
- Algèbre
- Analyse
- Algèbre
- Probabilités
SecondePremièreTerminale2BAC SM MarocMPSI/PCSI Physique-Chimie
Physique-Chimie Corrigés de BAC
Corrigés de BAC Révisions Maths lycée
Révisions Maths lycée Prépa Examens
Prépa Examens
Maths
Analyse
Première
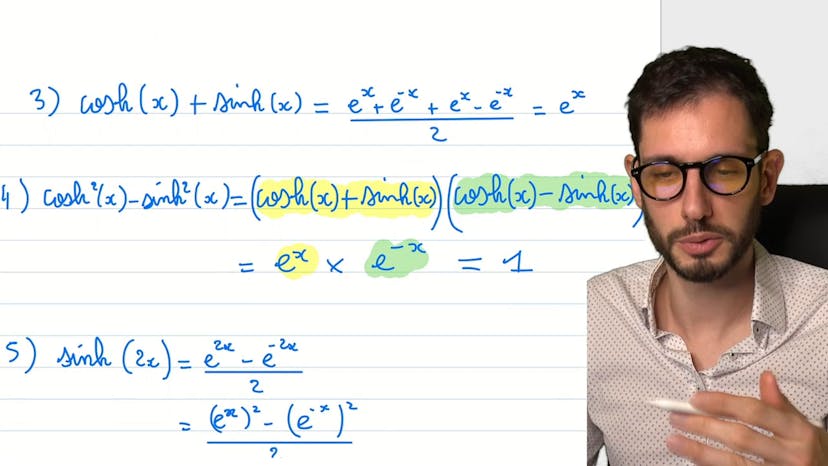
Cos et Sin hyperboliques !
Dans ce cours, nous étudions les fonctions cosinus et sinus hyperboliques, qui sont des fonctions courantes en physique et en maths pures de première année. Nous démontrons que cosinus hyperbolique (cosh) est pair et nous étudions ses variations sur l'intervalle 0 plus infini. Nous faisons de même pour le sinus hyperbolique (sinh). Nous étudions également quelques relations intéressantes entre les fonctions, telles que cosh plus sinh et cos² moins sin². Enfin, nous démontrons que deux fois le sinus hyperbolique de 2X est égal à la multiplication de cosinus hyperbolique et sinus hyperbolique de X.
Maths
Analyse
Première

Dérivabilité en 0 (1er exemple)
Dans cet exercice de mathématiques, on étudie la dérivabilité d'une fonction définie en deux parties. Tout d'abord, pour les valeurs différentes de 0, cette fonction est égale à l'expression e^(1/x) où x est non nul et positive. Ensuite, on ajoute la valeur f(0) = 0 à cette fonction pour l'étendre sur l'ensemble des réels. Pour étudier sa dérivabilité, on utilise deux méthodes. La première méthode est la méthode classique qui consiste à étudier un taux d'accroissement de la fonction en 0. On obtient ainsi que la fonction n'est pas dérivable en 0 car le taux d'accroissement admet une limite infinie. La seconde méthode utilise le graphique de la fonction pour montrer qu'elle n'est pas continue. Par conséquent, elle n'est pas dérivable. Deux méthodes simples pour étudier la dérivabilité d'une fonction mathématique en utilisant des concepts telles que les taux d'accroissement et la continuité de la fonction.
Maths
Analyse
Première
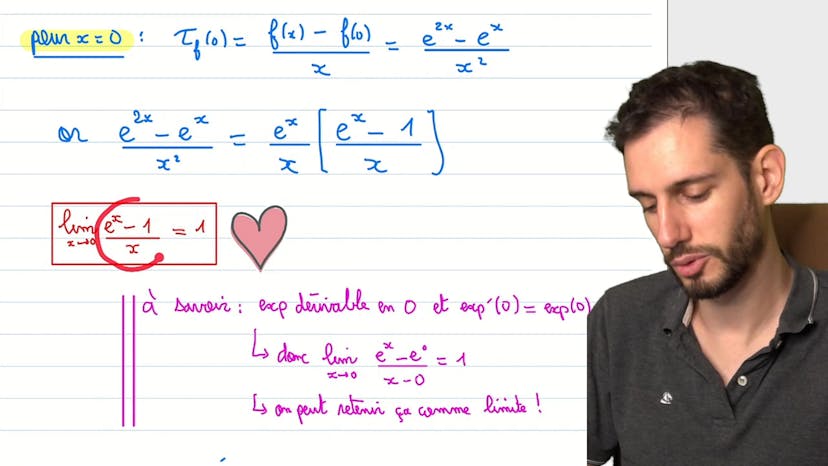
Dérivabilité en 0 (2ème exemple)
Dans cet exercice, on doit étudier la dérivabilité d'une fonction comprenant de l'exponentiel pour une valeur donnée en 0. La méthode consiste à calculer le taux d'accroissement en ce point et vérifier s'il admet une limite finie. On factorise ensuite le taux d'accroissement pour faire apparaître le ratio e2x-1 sur x, qui a une limite de 1 lorsque x tend vers 0. Cette limite est la définition de la dérivabilité de la fonction exponentielle en 0. En utilisant cela, on peut simplifier l'exercice et conclure que la fonction n'est pas dérivable en 0 car son taux d'accroissement tend vers plus ou moins l'infini en ce point.
Maths
Analyse
Première

Dériver 2 fois pour conclure !
Nous étudions une fonction complexe et examinons la méthode d'étude de fonction. Nous commençons par vérifier si la fonction est paire ou impaire, puis si elle est trivialement croissante ou décroissante. Ensuite, nous examinons la dérivée et étudions le signe de l'expression pour en déduire le signe de la fonction. Si nous ne pouvons pas simplifier l'expression de la dérivée, nous pouvons étudier la fonction elle-même pour en déduire son signe. Nous pouvons redériver la fonction pour avoir sa dérivée seconde et trouver les points de minimums ou maximums en cherchant ses racines. En utilisant cette méthode, nous pouvons résoudre des fonctions complexes et obtenir de meilleurs résultats aux contrôles.
Maths
Analyse
Première
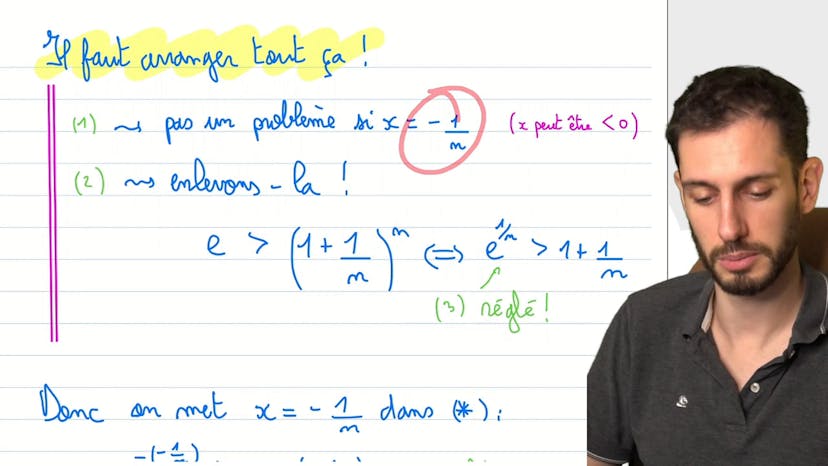
Encadrement de e par des suites
Cette transcription d'une vidéo explique comment trouver un encadrement de la constante E de l'Eve à partir d'un exercice en combinant l'exponentiel et la suite. Les deux premières questions portent sur le comportement de l'exponentiel par rapport à X, tandis que les questions suivantes impliquent des applications d'entiers et l'étude de suites. À la question 5, on doit montrer une inégalité avec de l'exponentiel et du X en utilisant une fonction. Enfin, à la question 6, on doit trouver un encadrement de E avec une amplitude de 10^-6 en utilisant les résultats des questions précédentes. Pour cela, on utilise une valeur de N telle que l'écart entre deux valeurs encadrant E est inférieur à 10^-6. Il est important de suivre la méthode étape par étape et de ne pas paniquer.
Maths
Analyse
Première

Calcul d'expressions 1
Ce cours explique comment calculer les sinus et cosinus pour des expressions qui dépendent de n en utilisant le cercle trigonométrique. Le cercle trigo est une manière de voir les angles en associant un angle à la longueur de cercle qu'il peut parcourir. Les longueurs d'arc associées à un angle ont la même valeur de cosinus-sinus et peuvent être associées à une certaine valeur π ou un nombre de cercles en plus. Les valeurs de cosinus et sinus pour les expressions 2nπ, 2n+1π et nπ sont déduites. Le résultat pour nπ dépend de n, avec un sinus de 0 et un cosinus de -1 ou 1 si n est pair ou impair respectivement. Enfin, une expression complexe est simplifiée pour trouver le cosinus et le sinus pour le point correspondant. Il est important de retenir que moins 1 puissance n correspond à 1 si n est pair et à -1 si n est impair pour nπ.
Maths
Analyse
Première
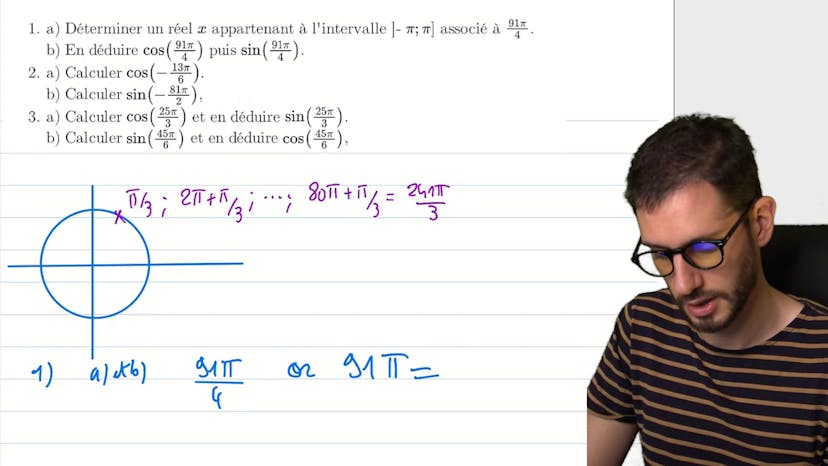
Calcul d'expressions 2
Apprendre les valeurs trigonométriques peut être simplifié en trouvant des valeurs équivalentes plus courantes. Par exemple, 241pi/3 peut être simplifié en pi/3 pour trouver les valeurs de cosinus et sinus. Pour trouver les valeurs pour 91pi/4, vous pouvez retirer des paquets de 2pi et exprimer 91pi/4 comme 10 paquets de 2pi plus 3pi/4. Les valeurs de cosinus et sinus pour 91pi/4 sont les mêmes que pour pi/4, mais avec des signes différents. Les questions 2a, b et 3a, b utilisent la même méthode.
Maths
Analyse
Première

Points sur le cercle trigo
Dans cet exercice sur le cercle trigonométrique, on doit placer des points astucieusement. Le point A associé au réel pi sur 3 est placé sur le cercle trigo. Ensuite, le point B symétrique de A par rapport à l'axe des abscisses est tracé. Les réels associés à ces points dans l'intervalle 0 de pi et dans l'intervalle moins pi pi sont demandés. Il y a une faute de français car ils veulent dire le réel associé à ce point dans chaque intervalle, pas les réels associés. Le nombre associé à A est pi sur 3, à B c'est 5 pi sur 3, et à C c'est 2 pi sur 3. Enfin, le point D symétrique de A par rapport à O est placé et le réel associé à ce point est 4 pi sur 3 entre 0 et 2 pi, et moins 2 pi sur 3 entre moins pi et pi. Il faut comprendre qu'on peut parcourir plusieurs tours et qu'un seul point du cercle peut représenter plusieurs nombres.
Maths
Analyse
Première
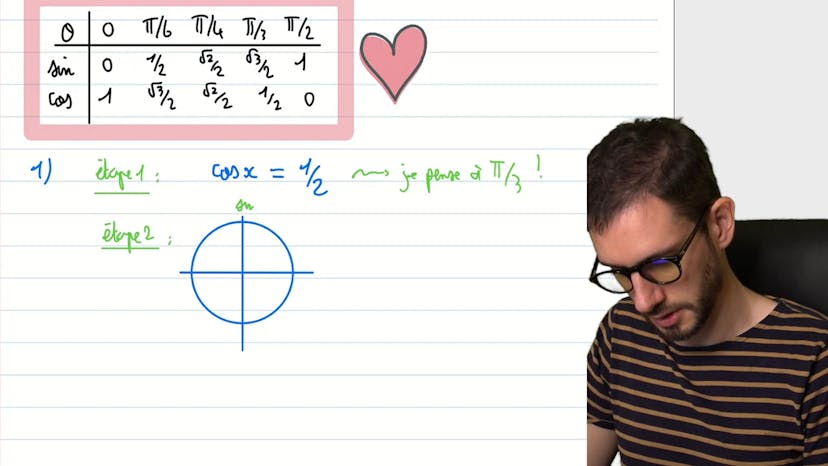
Equations trigos simples
La vidéo explique comment résoudre des équations trigonométriques simples en utilisant le cercle trigonométrique et le tableau des valeurs de sine et cosine. La première étape consiste à identifier la valeur classique à laquelle on peut se rapporter dans le problème. La deuxième étape consiste à tracer le cercle trigonométrique pour trouver les points où l'équation est vérifiée. Il est important de comprendre la contrainte de l'intervalle et de trouver les angles solutions dans cette plage. La vidéo illustre cet exemple pour résoudre 2cos(x) = 1 dans l'intervalle [0, 2π] avec les solutions x=π/3 et x=5π/3 et pour résoudre 2sin(x) = -1 avec les solutions x=7π/6 et x=11π/6 dans cet intervalle.
Maths
Analyse
Première

Inéquations trigos simples
Ce cours explique comment résoudre des inéquations en utilisant un tableau de valeurs de base. Le premier exemple montre comment réécrire une inéquation en utilisant le cosinus et la racine de 2. En traçant un cercle trigo et en utilisant le point pi sur 4, l'élève peut identifier les angles pour lesquels le cosinus est inférieur à pi sur 4, en excluant les points de l'axe des abscisses. L'ensemble des angles est entre moins pi et pi, en incluant moins pi sur 4 exclu et pi sur 4 exclu. Le deuxième exemple utilise la racine de 2 sinus x et se réécrit en utilisant la racine de 6, qui peut être simplifiée, et en utilisant le sinus. Le cercle trigo est tracé sur l'axe vertical, en utilisant le point pi sur 3. L'ensemble des angles avec un sinus supérieur à racine de 3 sur 2 est entre moins pi et pi et inclus pi sur 3 et 2 pi sur 3. En résumé, pour résoudre une inéquation, il faut transformer l'équation pour utiliser le tableau de valeurs, tracer un cercle trigo, puis lire les angles correspondants en parcourant l'ensemble donné.
Maths
Analyse
Première

Equation trigo où poser X=sinx
Dans ce cours, on apprend à résoudre une équation trigonométrique qui inclut cos et sin, ainsi que des termes cos² et sin². Pour simplifier l'équation, on utilise l'identité fondamentale de la trigonométrie pour remplacer cos² par 1-sin². Ensuite, on pose un grand X pour résoudre l'équation de degré 2 qui apparaît. Finalement, on revient à la trigonométrie pour trouver les solutions de l'équation d'origine en fonction de X. Les solutions en fonction de X forment un cercle trigo et l'ensemble des solutions réelles est obtenu en trouvant quand le sinus vaut 1.
Maths
Analyse
Première
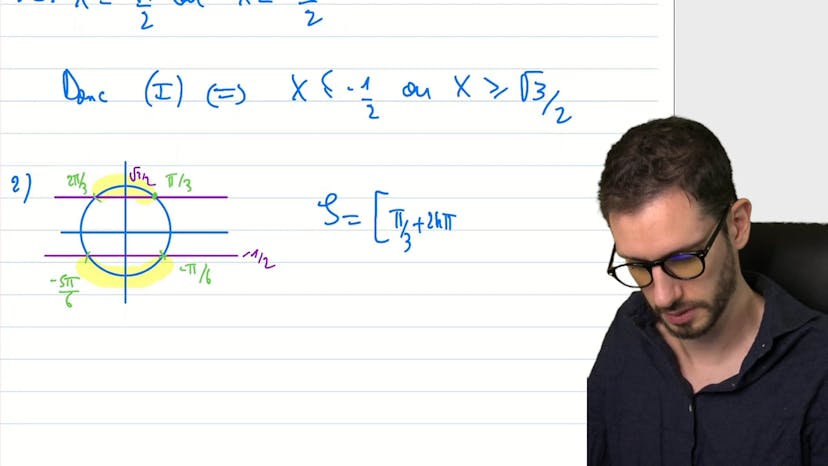
Inéquation trigo où poser X=sinx
Dans cette leçon de mathématiques, nous avons une équation avec seulement du sinus, donc pas besoin de faire un changement de variable. Nous résolvons l'équation en posant "X = sin(x)" et en trouvant les racines à partir de cela. Ensuite, nous utilisons une astuce pour résoudre l'inéquation qui nous est donnée. Nous rappelons également la méthode X2-XS+P pour trouver les racines d'une équation à deux degrés. Finalement, nous utilisons une méthode trigo pour trouver l'ensemble des solutions.


