Online Physique-Chimie Courses by Top Instructors

Iceberg

Dans cette vidéo, nous étudions les forces appliquées à un iceberg flottant à la surface de l'eau. L'iceberg a un volume total V-ice et un volume immergé V-im. Les forces agissant sur l'iceberg sont le poids, dirigé vers le bas, et la poussée d'Archimède, dirigée vers le haut. Le poids de l'iceberg peut être calculé en utilisant la formule classique M x G, où M est la masse de l'iceberg et G est l'accélération due à la gravité. La masse de l'iceberg est déterminée en multipliant la masse volumique de la glace par le volume de glace immergé. Ainsi, le poids de l'iceberg peut être exprimé comme moins la masse volumique de la glace multipliée par le volume de glace immergé et l'accélération due à la gravité, dans la direction opposée à l'axe vertical (représenté par le vecteur unitaire EZ). La poussée d'Archimède est un peu plus complexe à calculer. Elle est donnée par moins la masse de fluide déplacé par l'iceberg, multipliée par l'accélération due à la gravité. La masse de fluide déplacé est égale à la masse volumique de l'eau multipliée par le volume immergé de l'iceberg. Ainsi, la poussée d'Archimède peut être exprimée comme moins la masse volumique de l'eau multipliée par le volume immergé de l'iceberg et l'accélération due à la gravité, dans la direction opposée à l'axe vertical. En effectuant les calculs numériques, nous obtenons que le poids de l'iceberg est égal à la poussée d'Archimède, ce qui explique pourquoi l'iceberg ne se déplace pas verticalement et reste en équilibre sur l'eau. En résumé, les forces appliquées sur l'iceberg sont le poids dirigé vers le bas et la poussée d'Archimède dirigée vers le haut. Le poids peut être calculé en fonction de la masse volumique de la glace et du volume immergé de l'iceberg, tandis que la poussée d'Archimède dépend de la masse volumique de l'eau et du volume immergé de l'iceberg. Le poids et la poussée d'Archimède sont égaux en grandeur, ce qui maintient l'iceberg en équilibre sur l'eau.

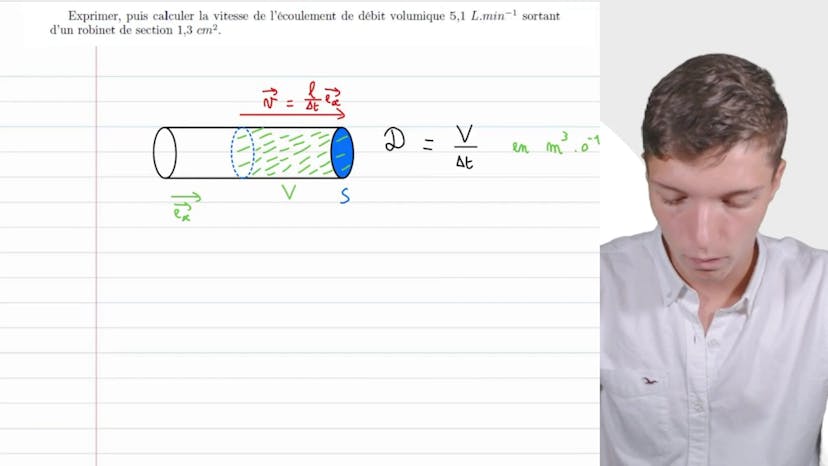
Débit d’un robinet

Dans cette vidéo, Matisse de Studio aborde le sujet du débit sortant d'un robinet. Il donne une définition du débit et explique comment calculer la vitesse d'écoulement en utilisant les grandeurs fournies. Il conseille de faire un schéma pour mieux comprendre le concept. Il représente la section du robinet et le volume d'eau qui traverse cette section pendant un intervalle de temps donné. Il introduit les notions de section dernière et de vitesse du fluide. En utilisant l'expression du volume, il relie le débit et la vitesse en exprimant que la vitesse est égale au débit divisé par la surface. Il indique également qu'il faut faire attention aux unités lors de l'application numérique. En appliquant les conversions nécessaires, Matisse trouve une vitesse d'écoulement de 0,65 mètres par seconde. Il conclut en encourageant les spectateurs à refaire cette démonstration pour mieux comprendre le sujet. Il souligne l'importance de savoir manipuler les schémas et les volumes qui traversent une section et affirme que maîtriser ces concepts permettra de résoudre n'importe quel exercice utilisant cette notion. Il remercie les spectateurs d'avoir suivi la vidéo et les salue en leur donnant rendez-vous prochainement.

Tuyau biscornu

Dans cette vidéo, Matisse de STUDIO explique comment calculer le débit volumique à travers trois sections d'un tuyau biscornu. Il utilise la formule du débit volumique qui est la vitesse du fluide multipliée par la surface de la section. En utilisant cette formule, il exprime les vitesses V1 et V2 en fonction des surfaces S0, S1, S2 et de la vitesse V0. Il explique ensuite que la conservation du débit volumique permet de comprendre que le fluide s'écoule plus rapidement dans les sections plus étroites. Ensuite, il utilise la relation de Bernoulli pour exprimer la pression sur chaque surface S1 et S2 en fonction de la pression P0, de la vitesse V0 et des autres paramètres du système. Il montre comment utiliser cette relation pour calculer les pressions P1 et P2. Il conclut en soulignant l'importance de comprendre cette méthode dans le domaine du débit volumique.

Étude du sang

Dans cette vidéo, Matisse de Studio explique le processus de circulation du sang dans le corps humain. Il commence par parler de l'aorte, l'artère principale qui sort du cœur et qui a un diamètre de 32mm. Dans l'aorte, le sang circule à une vitesse moyenne de 50cm par seconde. Ensuite, l'aorte se divise en artères plus petites appelées artérioles, où la vitesse de circulation du sang est de 20cm par seconde. L'objectif est de calculer la surface totale de section des artérioles, en utilisant le concept de débit volumique. On utilise la formule du débit volumique, qui est la vitesse du sang multipliée par la section qu'il traverse. On calcule donc la surface de l'aorte à partir de son diamètre (pi * r²), puis on isole la surface totale des artérioles en utilisant les vitesses v1 et v2. Le résultat numérique est de 2 * 10^-3 mètres carrés, ce qui est une surface plus grande car le sang circule moins vite. Ensuite, les artérioles se divisent en capillaires, qui ont une surface totale de section de 4000cm². On nous demande de calculer la vitesse du sang dans un capillaire. On utilise à nouveau la même méthode, en utilisant les vitesses v2 et v3, et on isole v3 en fonction des surfaces des artérioles et des capillaires. Le résultat numérique est de 0,01 cm par seconde. Cette vitesse est très faible car la surface totale des capillaires est beaucoup plus grande que celle des artérioles, ce qui conserve le débit volumique. En conclusion, cette vidéo donne une explication détaillée sur le processus de circulation du sang et explique comment calculer différentes grandeurs en utilisant le concept de débit volumique.

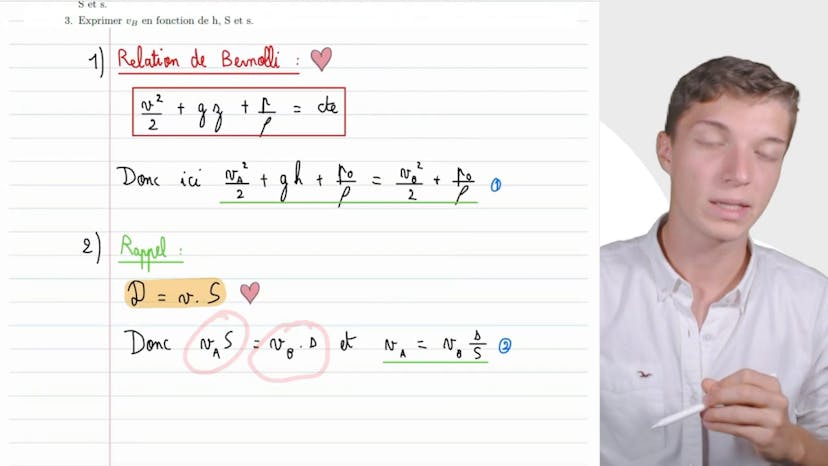
Vidange

Dans cette vidéo, Matisse de Studio aborde un exercice classique de mécanique des fluides qui concerne la vidange d'un vase percé. Il commence par mentionner que la pression en A et en B est identique à la pression atmosphérique. En utilisant la relation de Bernoulli, il exprime cette relation entre les points A et B. Ensuite, il utilise la conservation du débit volumique pour exprimer la vitesse VA en fonction de la vitesse VB, de la section S et de la section s. Enfin, il combine les deux expressions précédentes pour exprimer VB en fonction de la profondeur h, de la section S et de la section s. Il conclut en disant que cet exercice combine les deux relations les plus importantes en mécanique des fluides et encourage les spectateurs à le revoir et à le comprendre en détail.

Supertanker

Le Sea-Way Giant est le supertanker le plus grand jamais construit, avec des dimensions de 458 mètres de long, 60 mètres de large et une hauteur moyenne de 32 mètres. Lorsqu'il est vide, il s'enfonce de 3 mètres dans l'eau. Pour calculer la masse du supertanker, on utilise le principe fondamental de la dynamique. Les forces qu'il subit sont son poids et la poussée d'Archimède. En exprimant ces forces, on obtient la masse du supertanker, qui est égale à la masse volumique de l'eau multipliée par le volume d'eau déplacé par le supertanker. Ensuite, on considère le supertanker rempli de pétrole brut. La démarche est similaire, mais cette fois-ci, on doit déterminer la hauteur à laquelle le supertanker s'enfonce dans l'eau. En utilisant à nouveau le principe fondamental de la dynamique, on obtient une hauteur d'enfoncement de 22 mètres. Il est important pour les ingénieurs de prendre en compte ce type de calculs lors de la conception des navires.

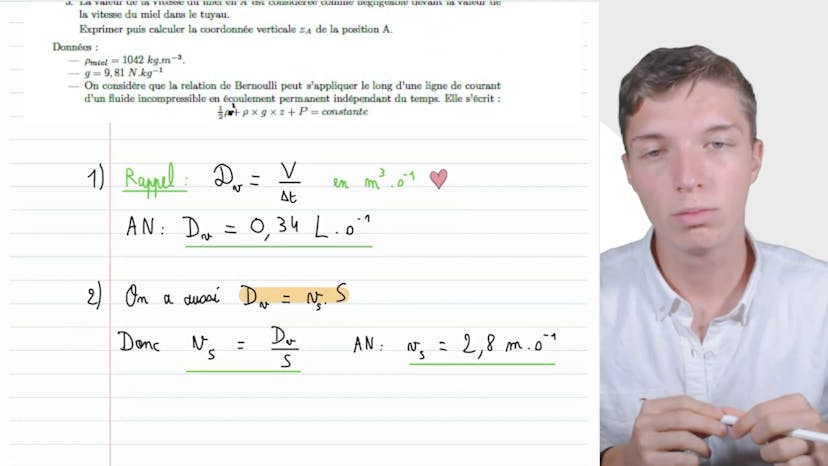
Écoulement du miel

Dans cette vidéo, Matisse de Studio nous parle de l'écoulement du miel. Il explique que dans une laiterie, du miel s'écoule d'un réservoir vers une cuve de lait à travers un tuyau de diamètre 12,5 mm. Il mentionne que pour simplifier les calculs, on néglige la viscosité du miel, bien que cela soit une hypothèse forte. Matisse pose ensuite trois questions. La première concerne la durée de remplissage de la cuve, qui fait 41 litres de miel en 2 minutes. Le débit volumique d'écoulement du miel dans la cuve est calculé en utilisant la formule du débit volumique, ce qui donne une valeur de 0,34 litres par seconde. La deuxième question consiste à calculer la vitesse d'écoulement du miel dans le tuyau. Pour cela, on utilise l'autre expression du débit volumique, qui est égal à la vitesse d'écoulement multipliée par la section de la sortie du tuyau. On obtient une valeur de 2,8 mètres par seconde. Enfin, la troisième question concerne la coordonnée verticale de la position a du miel. En utilisant la relation de Bernoulli, on obtient une formule pour trouver cette coordonnée. En appliquant cette formule, on trouve que l'altitude du point a est de 0,9 mètre. En conclusion, Matisse nous remercie d'avoir suivi la vidéo et nous donne rendez-vous pour la prochaine fois.

Pression nul

Dans cette vidéo, Matisse de Studio aborde le problème des cas particuliers où la pression s'annule dans un écoulement, ce qui peut provoquer la formation de bulles et perturber le débit. Il commence par rappeler la loi de Bernoulli et la relation de conservation du débit. En utilisant ces équations, il exprime la pression P1 en fonction des autres paramètres. En simplifiant les termes, il obtient l'équation suivante : V02/2 + P0/ρ = V12/2 + P1/ρ. Ensuite, en utilisant la conservation du débit (D = V * S), il montre que V1 peut être exprimée en fonction de V0 et des différentes sections (S0 et S1). En simplifiant cette équation, il obtient V1 = V0 * S0/S1. Il utilise ensuite cette expression pour réécrire l'équation de Bernoulli en fonction de V0, S0, S1, P0 et P1. Après simplification, il obtient V02/2 + P0/ρ = V02*S0²/S1² + P1/ρ. Il poursuit en supposant que la pression P1 s'annule, ce qui permet de supprimer ce terme dans l'équation. En inversant les termes, il obtient finalement une expression pour la vitesse V0 à partir de laquelle la pression P1 s'annule : V0 = √(P0/(2ρ * (S0²/S1² - 1))). En résumé, cette vidéo aborde le problème des cas où la pression s'annule dans un écoulement. En utilisant la loi de Bernoulli et la relation de conservation du débit, Matisse parvient à exprimer la pression P1 en fonction des autres paramètres. Il montre ensuite comment calculer la vitesse à partir de laquelle la pression P1 s'annule.

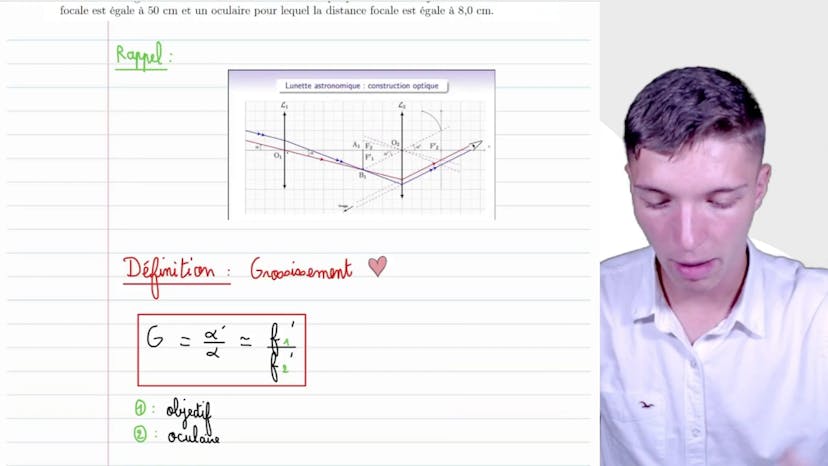
Grossissement

Dans cette vidéo, on aborde le sujet de la lunette astronomique et on se concentre sur le calcul du grossissement. Pour cela, on nous donne les valeurs de la distance focale de l'objectif (50 cm) et de l'oculaire (8 cm). Avant de passer au calcul, on présente brièvement la lunette astronomique. Elle est composée d'un objectif, qui est la première lentille convergente rencontrée par les rayons lumineux, et d'un oculaire, qui est la deuxième lentille convergente permettant de faire converger les rayons vers l'œil de l'observateur. Le foyer F2 de l'oculaire est confondu avec le foyer image F1 de l'objectif, ce qui rend le montage afocal. En ce qui concerne le calcul du grossissement, on utilise la formule classique : le grossissement est égal à l'angle alpha prime sous lequel on observe les rayons sortant de l'oculaire, divisé par l'angle alpha incident des rayons par rapport à l'axe optique arrivant sur l'objectif. Cependant, cette formule peut être approximée pour des angles très petits et équivaut à F1' / F2'. F1' représente la distance focale de l'objectif et F2' représente la distance focale de l'oculaire. Le grossissement est donc égal à F1' / F2'. Dans cet exercice, le grossissement est de 6,3. En conclusion, on a ainsi calculé le grossissement d'une lunette astronomique en utilisant les valeurs des distances focales de l'objectif et de l'oculaire. Le grossissement est une mesure importante en physique pour ce type d'objet. Merci d'avoir suivi la vidéo et à bientôt !

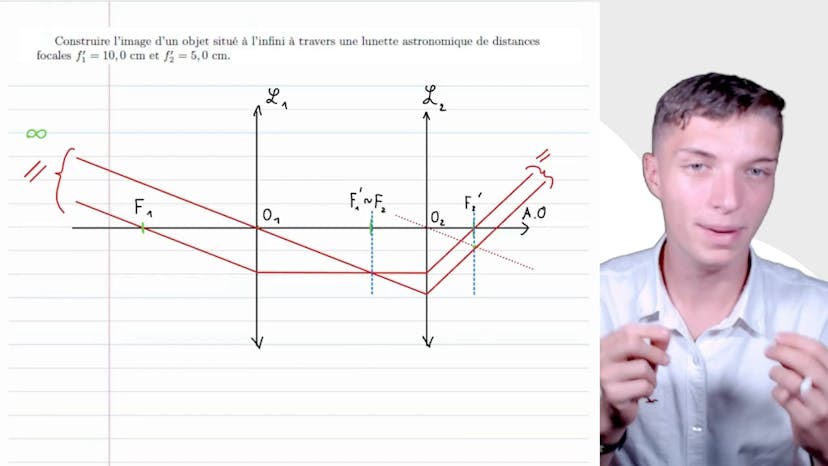
Schéma

Dans cette vidéo, Matisse de Studio explique le trajet d'un rayon lumineux à travers une lunette astronomique. La lunette est composée de deux lentilles convergentes, avec des distances focales f1' et f2'. Le foyer image de la première lentille est confondu avec le foyer objet de la deuxième lentille, ce qui rend le montage AFOC. Pour construire l'image d'un objet situé à l'infini, il faut tracer deux rayons. Le premier rayon passe par l'axe optique de la première lentille sans être dévié. Le deuxième rayon passe par le foyer image de la première lentille et est parallèle au premier rayon. Ensuite, le premier rayon entre dans la deuxième lentille parallèlement à l'axe optique, tandis que le deuxième rayon est tracé parallèlement à l'axe optique et passe par le centre de la deuxième lentille. L'intersection de ces deux droites donne la position de l'image de l'objet. Dans le cas d'une lunette astronomique, les rayons sortent de manière parallèle, ce qui donne l'impression de regarder l'infini. Il est important de refaire ce schéma plusieurs fois pour bien comprendre le tracé des rayons. Merci d'avoir suivi cette vidéo et à bientôt.

Zoom

Aucun résumé n'est disponible pour cette vidéo