Intro Convergence

Dans ce cours sur les théorèmes de convergence, on parle de suites qui peuvent être difficiles à gérer et qui semblent inexcessibles. Cependant, certaines de ces suites sont en réalité assez proches de zéro. On peut donc avoir l'intuition que ces suites vont converger vers zéro. Pour illustrer cela, le professeur montre un graphique montrant la fonction sin(x) ainsi que les différents points de la suite en question, qui convergent effectivement vers zéro. 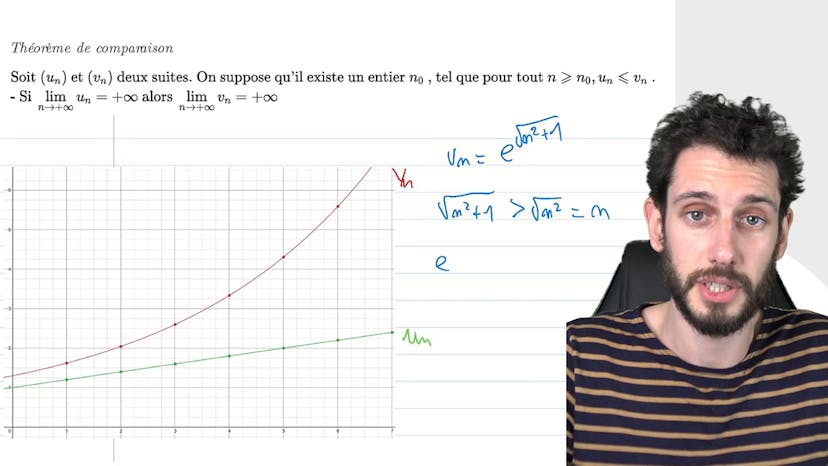En termes mathématiques, les théorèmes de convergence nous permettent d'analyser ces suites en utilisant d'autres suites plus simples et classiques. Deux théorèmes importants pour cela sont le théorème de comparaison, qui permet de montrer qu'une suite tend vers l'infini, et le théorème de gendarme, qui permet de montrer qu'une suite tend vers une limite finie. On étudiera également les notions de suites minorées, majorées et bornées, ainsi que le théorème de convergence monotone, qui est essentiel en terminale. En termes de méthodes, on apprendra à gérer les sinus de n, les termes du type (-1)^n, et les suites homographiques, qui sont fréquemment rencontrées dans les exercices. Ce cours est accessible et clair, contrairement aux définitions de limites qui peuvent sembler plus compliquées. N'hésitez pas à poser vos questions dans la FAQ si vous avez besoin de précisions. La prochaine vidéo portera sur le théorème de comparaison.