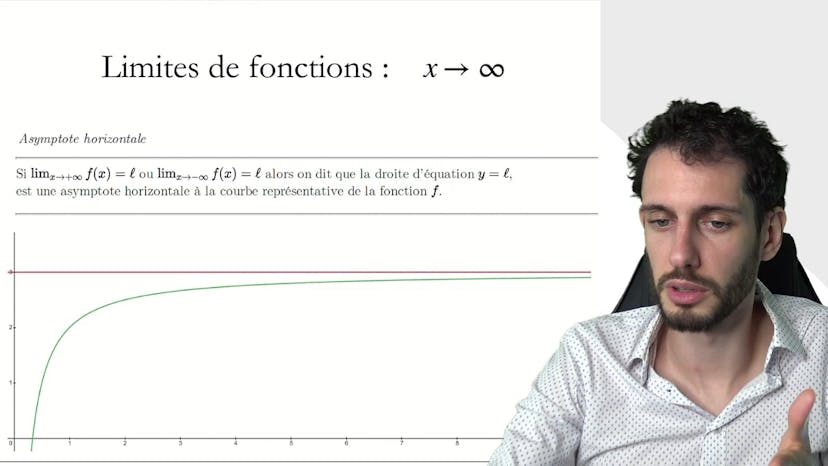
Determiner une asymptote + étude

Dans ce cours, nous apprenons à trouver les asymptotes d'une fonction. Les asymptotes peuvent être situées à moins l'infini, à plus l'infini, aux deux, ou sur les bords de l'ensemble de définition de la fonction. Pour trouver ces asymptotes, nous devons prendre en compte les valeurs interdites de la fonction. Dans l'exemple donné, la fonction f(x) est égale à -2/(1-x) et est définie sur R privé de 1. Nous regardons d'abord les asymptotes à moins l'infini et à plus l'infini. En utilisant le quotient, nous constatons que f(x) tend vers moins l'infini à x=0. Par conséquent, nous avons une asymptote horizontale y=0 pour les valeurs extrêmes. En analysant la fonction en x=1, nous constatons que 1-x tend vers 0 en approchant x de 1 par la gauche et par la droite. En utilisant le quotient, nous déterminons que f(x) tend vers moins l'infini en s'approchant de 1 par la gauche et vers plus l'infini en s'approchant de 1 par la droite. Ainsi, nous avons une asymptote verticale x=1 pour cette valeur interdite. En résumé, pour trouver les asymptotes, nous examinons les tendances à plus l'infini, à moins l'infini et sur les bords de l'ensemble de définition de la fonction.