Calcul de limite infinie avec la définition (trouver un A)

Dans ce cours, nous abordons la définition formelle de la limite. Il s'agit d'un concept important en mathématiques, qui peut être difficile à comprendre au début. La limite d'une fonction consiste à dire que lorsque la variable x tend vers l'infini, la valeur de la fonction tend également vers l'infini. En d'autres termes, peu importe la valeur à laquelle je fixe ma hauteur, il y aura toujours un moment où la fonction la dépassera et restera toujours au-dessus. 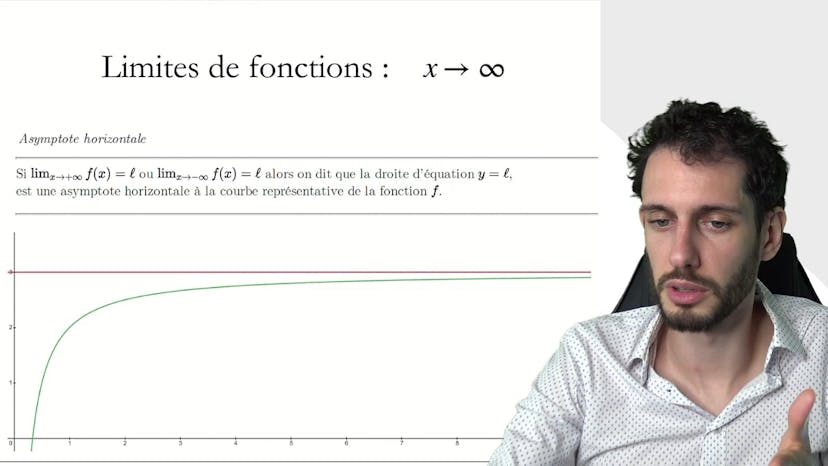Pour illustrer cela, nous avons tracé une fonction de type racine carrée de x. Peu importe la valeur choisie pour m, il y aura toujours une valeur a à partir de laquelle la fonction sera au-dessus de cette hauteur. Ensuite, nous appliquons cette définition à un exemple spécifique où f(x) est égal à la racine carrée de x^2 -1. Nous devons montrer l'existence d'un a pour chaque valeur de m. Pour cela, nous résolvons l'inéquation f(x) > m. En passant au carré, nous obtenons x^2 > m + 1. En gardant à l'esprit que nous nous intéressons à la limite vers l'infini, nous prenons la solution positive et obtenons x > racine carrée de m^2 + 1. Cela nous permet de trouver la valeur a appropriée. En utilisant cette valeur dans l'autre sens, nous pouvons montrer que f(x) > m lorsque x > a. Cela confirme que la fonction tend bien vers l'infini lorsque x tend vers l'infini. Il est important de s'exercer avec différentes fonctions pour maîtriser cette méthode de résolution d'équations et de retrouver la valeur a correspondante. Au final, il s'agit simplement d'appliquer la définition formelle de la limite.