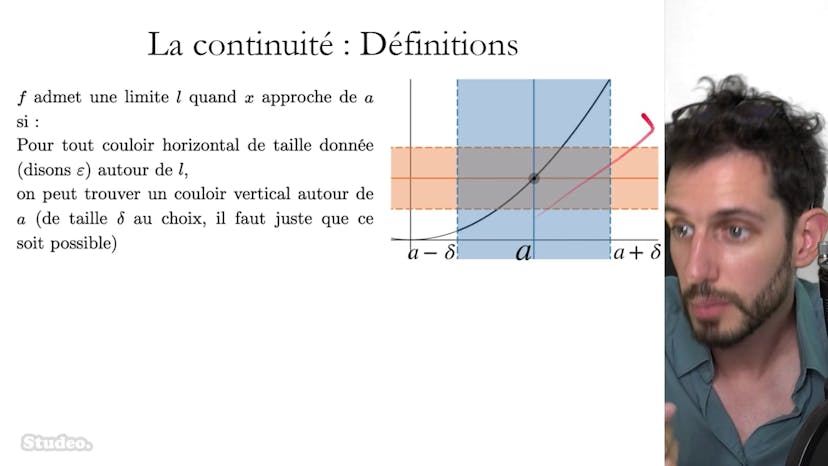
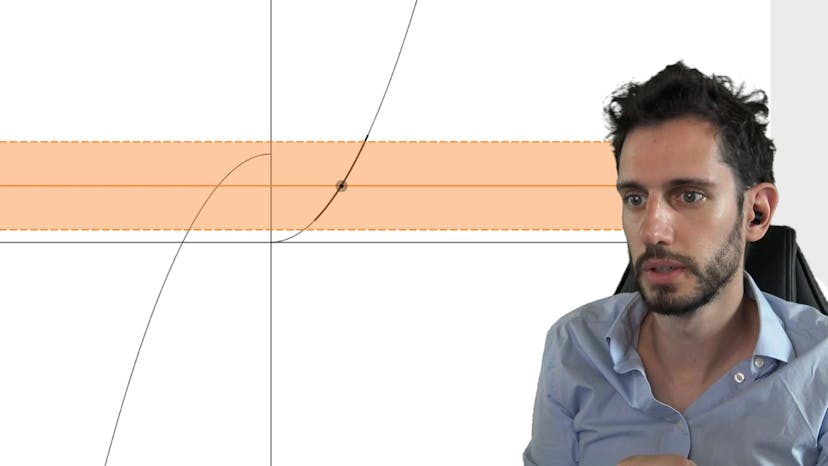
Prolongement par Continuité

Dans ce cours, nous abordons le concept de prolongement par continuité en mathématiques. Dans certains cas, une fonction peut ne pas être définie en un certain point, mais si la limite de cette fonction existe et est finie, il est possible de prolonger cette fonction par continuité en ce point. Pour ce faire, on pose la valeur de la fonction en ce point égal à la limite de la fonction quand x se rapproche de ce point. Ainsi, on crée une fonction qui est définie et continue en ce point. Par exemple, si nous considérons la fonction f(x) = x/x, cette fonction n'est pas définie en 0 à cause du dénominateur, mais on peut prolonger cette fonction par continuité en posant f(0) = 1. Ainsi, la fonction est définie et continue en 0. Dans un autre exemple, on nous propose une fonction f(x) = {x sin(1/x) si x ≠ 0, 0 si x = 0}. Cette fonction n'est pas définie en 0 à cause du terme 1/x, mais on peut conjecturer que cette fonction est continue en 0 en observant son graphique. Pour prouver cela, nous utilisons le théorème d'encadrement en utilisant la valeur absolue pour encadrer le sinus. Nous montrons alors que la fonction tend vers 0 en utilisant le théorème d'encadrement, ce qui prouve que la fonction est bien continuée en 0. En utilisant cette méthode de prolongement par continuité, nous pouvons donc étendre la définition d'une fonction et l'assurer continues en des points où elle n'était pas initialement définie.