TVI et Fonction Auxiliaire

Le cours aborde le théorème des valeurs intermédiaires en utilisant l'étude d'une fonction spécifique. La fonction f(x) est définie comme étant égale à 10x sur e^x plus 1. L'ensemble de définition de la fonction est [0, +∞) car le dénominateur, e^x plus 1, est strictement positif pour toutes les valeurs de x dans cet intervalle. La première étape consiste à vérifier que la fonction est bien définie et dérivable sur son ensemble de définition. Comme e^x plus 1 ne s'annule jamais à cause de l'exponentiel et du plus 1, il n'y a aucun problème et la fonction est donc bien définie et dérivable. En calculant la dérivée de la fonction f(x), on obtient f'(x) = (1 - x)e^x. On utilise ensuite cette dérivée pour déterminer les variations de la fonction f. En étudiant le signe de chaque facteur de la dérivée, on trouve que f'(x) est strictement négatif pour tout x dans l'intervalle [0, +∞), ce qui implique que la fonction f est strictement décroissante sur cet intervalle. 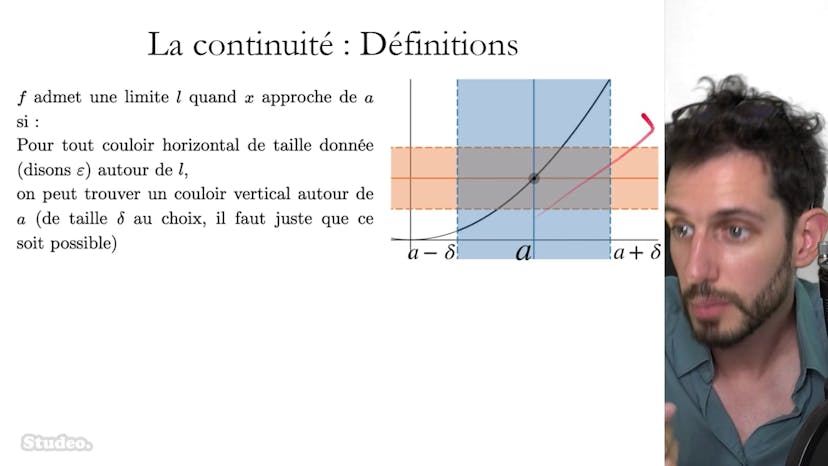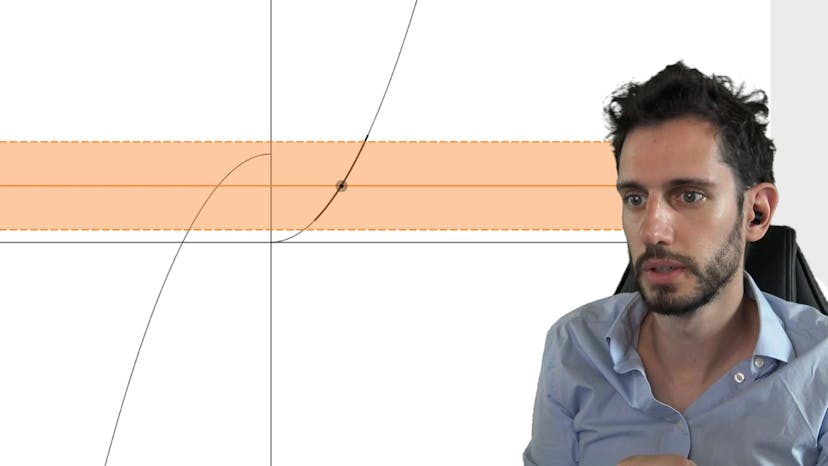Selon le théorème des valeurs intermédiaires, on démontre qu'il existe un unique réel alpha tel que f(alpha) = 0. Cette démonstration s'appuie sur la continuité de la fonction f sur son ensemble de définition, ainsi que sur le fait que la fonction est strictement décroissante. Pour trouver une estimation de la valeur de alpha, on peut utiliser une calculatrice pour encadrer la valeur de alpha entre deux réels donnés. Dans cet exemple, on trouve que alpha est compris entre 1,28 et 1,29. En étudiant le signe de la fonction f selon les valeurs de x, on constate que f est positive sur l'intervalle [0, alpha] et négative sur l'intervalle [alpha, +∞). Cette information permet de dresser le tableau de variations de la fonction f. Les limites de la fonction f sont également étudiées. On trouve que f(0) = 0 et que la limite de f(x) lorsque x tend vers l'infini est 0. Cela signifie que la fonction f a une asymptote horizontale y = 0. En conclusion, le cours explique comment appliquer le théorème des valeurs intermédiaires en utilisant une fonction auxiliaire pour étudier une fonction plus complexe. Il souligne également l'importance de la stricte monotonie dans l'unicité des solutions.